 |
Решение уравнений с использованием геометрической интерпретации
|
|
|
|
Геометрический смысл выражения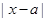 
--- длина отрезка координатной оси, соединяющего точки с абсциссами 
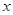и 
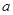. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример Решим уравнение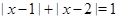 
.
Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой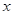 
до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка 
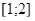обладают требуемым свойством, а точки, расположенные вне этого отрезка,--- нет.
Ответ.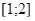 
.
Пример Решим уравнение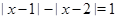 
.
Решение. Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2.
Ответ.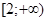 
.
Пример Решить неравенство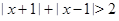 
.
Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек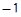 
и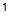 
в точности равна 
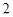. Это все точки отрезка 
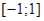. Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
Ответ.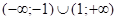 
.
Замечание. Обобщением решения вышеприведенных уравнений являются следующие равносильные переходы:
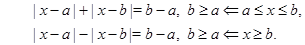
Пример Решите неравенство: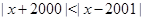 
.
Решение. Решим неравенство, используя координатную прямую. Данное неравенство выполняется для всех точек c координатой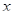 
, которые находятся ближе к точке с координатой 
, чем к точке с координатой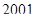 
. Так как 
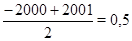, то искомыми являются все точки, расположенные левее точки с координатой 
.
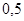Ответ.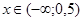 
.
Пример Решите уравнение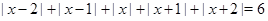 
.
Решение. Рассмотрим на числовой прямой точку с координатой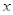 
. Сумма 
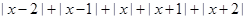равна сумме расстояний от точки 
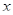до точек с координатами 2, 1, 0, -1, -2. Заметим, что сумма расстояний от любой точки до точек 
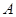и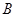 
не меньше длины отрезка 
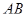(и равенство достигается тогда и только тогда, когда точка расположена на отрезке 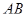). Отсюда получаем, что 
не меньше 4, а 
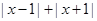не меньше 2 при любом 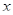. Поэтому для того, чтобы сумма 
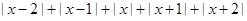была равна 
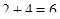, необходимо, чтобы 
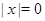. Итак, 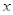необходимо равен 
. Легко проверить, что значение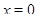 
действительно является решением данного уравнения.
|
|
|
Ответ. .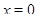
Пример Гальперин Г.А. Положительные числа , ,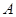 
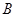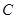и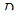 
таковы, что система уравнений
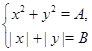
имеет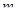 
решений, а система уравнений
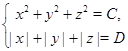
имеет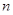 
решений. Известно, что 
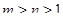. Найдите 
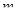и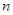 
.
Решение. Первое уравнение есть уравнение окружности, второму удовлетворяют точки квадрата с центром в начале координат и с диагоналями, принадлежащими осям координат. Система из двух первых уравнений в зависимости от 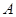и 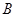либо не имеет решений, либо имеет четыре решения, либо восемь. Итак, 
может равняться либо 0, либо 4, либо 8. Первое уравнение второй системы есть уравнение сферы. Второму удовлетворяют точки октаэдра с центром в начале координат и с вершинами, лежащими на осях координат на равных расстояниях от центра. Эта система в зависимости от 
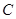и 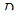либо не имеет решений, либо имеет 6 решений (вершины октаэдра лежат на сфере), либо имеет 8 решений (сфера касается граней октаэдра), либо имеет бесконечное число решений (сфера пересекает грани октаэдра по окружностям или нескольким дугам окружностей). Итак, 
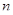может равняться либо 0, либо 6, либо 8, либо 
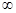. Условию 
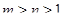удовлетворяет только вариант 
, 
.
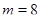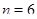Ответ. , .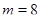
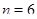Перевод алгебраической задачи на геометрический язык --- удобный и мощный метод решения задач. В качестве еще одного примера разберем блок задач олимпиады математико-механического факультета СПбГУ:
Пример Дана функция: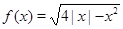 
.
а) Решите уравнение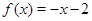 
;
б) Решите неравенство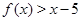 
;
в) Найдите количество решений уравнения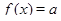 
в зависимости от значений параметра 
.
|
|
|
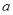Решение. Построим график функции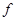 
. Для этого заметим, что 
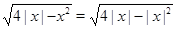, а тогда мы можем сначала построить график функции 
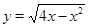, и затем отразить его относительно оси ординат. Преобразуем выражение, задающее функцию 
:
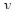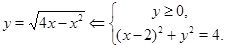
Поскольку данная система определяет верхнюю полуокружность радиуса 2 с центром в точке (2; 0), график исходной функции представляет собой объединение двух полуокружностей (см. рис.).
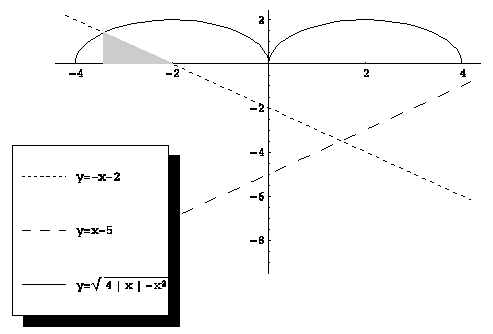
Теперь решение задач не представляет труда:
а) Корень уравнения есть абсцисса точки пересечения прямой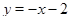 
с графиком функции 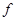. Найдем ее геометрически: заштрихованный на рисунке прямоугольный треугольник является равнобедренным (угловой коэффициент прямой равен 
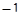), его гипотенуза есть радиус окружности, ее длина 2. Тогда длина катета, лежащего на оси абсцисс, есть 
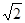, а искомая абсцисса равна 
.
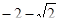б) Неравенство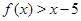 
выполнено при всех 
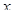из отрезка 
.
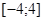в) При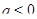 
, 
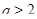решений нет, при 
уравнение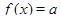 
имеет три решения, при 
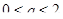--- четыре решения, при 
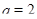--- два решения.
Решение уравнений с использованием тождества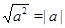 
Пример Решить уравнение
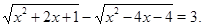
Решение. Дважды применяя тождество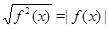 
, получим уравнение
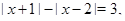
решением которого является интервал .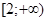
Ответ. .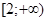
Пример Решить уравнение
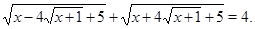
Решение.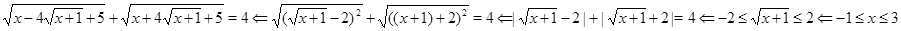 
.
Ответ.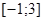 
.
|
|
|
