 |
Графики функций, содержащих линейные выражения под знаком абсолютной величины
|
|
|
|
Сформулируем утверждение, позволяющее строить график алгебраической суммы модулей, не раскрывая модули (это особенно удобно, когда модулей много).
Теорема Алгебраическая сумма модулей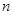 
линейных выражений представляет собой кусочно-линейную, график которой состоит из 
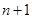прямолинейного участка. Поэтому график может быть построен по 
точкам, 
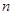из которых представляют собой корни внутримодульных выражений, ещё одна --- произвольная точка, с абсциссой меньше наименьшего из этих корней, и последняя --- с абсциссой, большей наибольшего из этих корней.
Замечание. Аналогично можно строить графики вида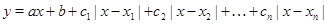 
.
Примеры построения графиков
1. 
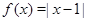. Вычисляем значения функции в точках 1, 0 и 2, получаем график, состоящий из двух лучей (см. рис.).
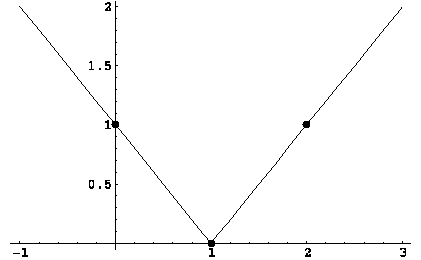
2. 
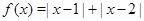. Вычисляя значение функции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из отрезка и двух лучей (см. рис.).
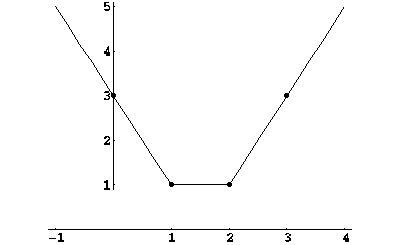
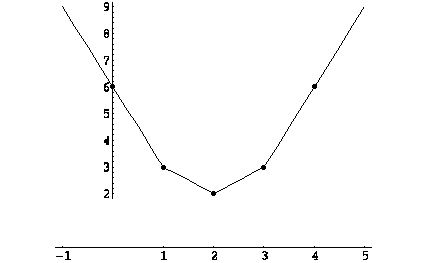
3. 
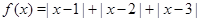. Для построения графика ``по отрезкам'' вычислим значение функции в точках 1, 2, 3, 0, 4 (см. рис.).
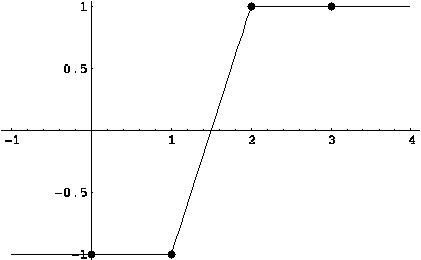
4. 
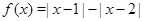. График разности модулей строиться аналогично (см. рис.).
Анализируя вид графиков 1, 2 и 3, можно предположить, а затем и доказать, что сумма модулей линейных выражений вида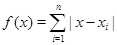 
достигает своего наименьшего значения либо в единственной точке, если число модулей нечетно, либо во всех точках некоторого отрезка, если число модулей чётно. График суммы нечетного числа модулей линейных выражений имеет форму клина, а график суммы чётного числа модулей имеет участок параллельный оси абсцисс. Более точно:
Теорема Пусть корни подмодульных выражений упорядочены по возрастанию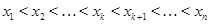 
. Тогда если число слагаемых 
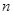нечётно и 
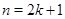, то наименьшее значение функции 
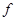достигается в точке 
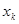, а если число слагаемых 
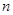чётно и 
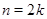, то наименьшее значение функции достигается во всех точках отрезка 
.
|
|
|
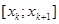Используем утверждение для решения задачи, предлагавшейся на одной из олимпиад Санкт-Петербургского государственного университета.
Пример В зависимости от значения параметра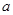 
, найти количество корней уравнения
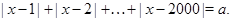
Решение. Решим задачу графически. Пусть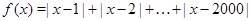 
, определим количество точек пересечения графика функции 
и прямой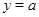 
в зависимости от 
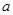. Исходя из сформулированного выше утверждения, график функции 
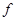будет иметь участок, параллельный оси абсцисс. Заметим, что абсциссы точек этого участка составляют отрезок 
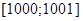, и во всех его точках функция достигает наименьшего значения, равного, например, 
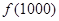, причем
Поскольку указанная сумма представляет собой удвоенную арифметическую прогрессию с первым членом 1, последним членом 999, сложенную с числом 1000, то она равна
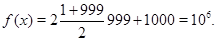
Тогда при 
уравнение не будет иметь решений, при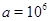 
их будет бесконечно много, а при 
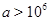уравнение будет иметь два решения.
Иные способы решения уравнений и неравенств с модулем
Метод раскрытия модулей
Метод раскрытия модулей рассмотрим на примере:
Пример Решить уравнение
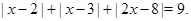
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1. Найти значения переменной, при которых каждый из модулей обращается в нуль: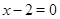 
, 
; 
, 
; 
, 
.
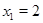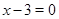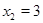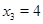2. Отметить эти точки на числовой прямой.
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1) Пр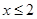и 
или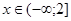 
. Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение 
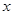из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех 
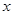из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях 
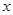из этого промежутка выражение будет положительным.
|
|
|
Возьмем значение 
из промежутка 
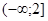и подставим его значение в выражение 
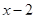, получаем 
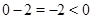, значит на этом промежутке 
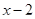отрицательно, а следовательно ``выйдет'' из под модуля со знаком ``минус'', получим: 
.
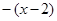При этом значении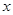 
, выражение 
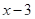получит значение 
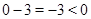, значит, оно на промежутке 
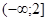также принимает отрицательные значения и ``выйдет'' из модуля со знаком ``минус'', получим: 
.
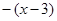Выражение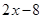 
получит значение 
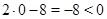и ``выйдет'' из под модуля со знаком ``минус'': 
.
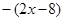Уравнение на этом промежутке получится таким: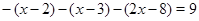 
, решая его, находим: 
.
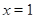Выясняем, входит ли это значение в промежуток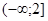 
. Оказывается входит, значит 
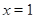является корнем уравнения.
2) При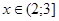 
. Выбираем любое значение 
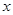из этого промежутка. Пусть 
. Определяем знак каждого из выражений под модулем при этом значении 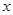. Оказывается, что выражение 
положительно, а два других отрицательны.
Уравнение на этом промежутке примет вид: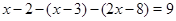 
. Решая его, находим 
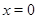. Это значение не входит в промежуток 
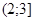, а значит, не является корнем уравнения.
3) При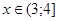 
. Выбираем произвольное значение 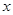из этого промежутка, скажем, 
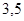и подставляем в каждое из выражений. Находим, что выражения 
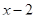и 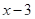положительны, а 
--- отрицательно. Получим следующее уравнение: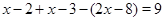 
.
После преобразования, получим: 
, а значит, уравнение не имеет корней на этом промежутке.
4) При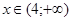 
. Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: 
, 
, 
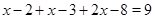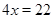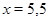которое входит в промежуток и является корнем уравнения.
Ответ.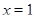 
, 
.
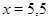Пример Решить уравнение
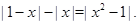
Решение.
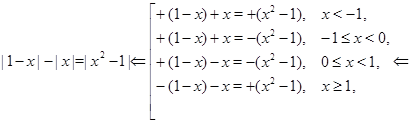
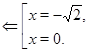
Ответ.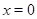 
, 
.
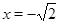Использование тождества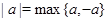 
, при решении уравнений
Из сформулированного свойства модуля можно вывести два полезных следствия:
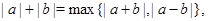
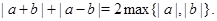
Проиллюстрируем применение первого из них для решения задачи вступительного экзамена в Санкт-Петербургский государственный университет.
Пример Изобразить график функции
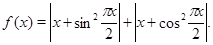
Решение. Перепишем задающую функцию выражение, используя первое следствие:
.
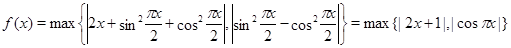Осталось только построить графики функций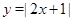 
, 
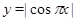в одной системе координат и определить участки, на которых один из них выше другого (см. рис.).
|
|
|
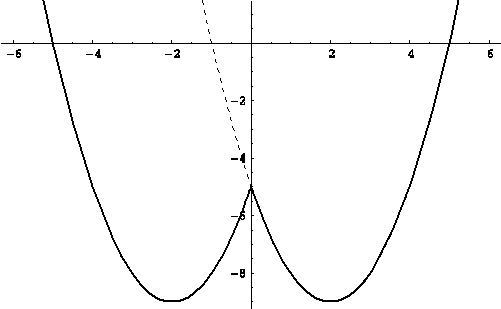
Использование второго тождества удобно для построения графика функции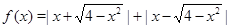 
.
Решение. В силу второго тождества, выражение задающее функцию, записывается в виде: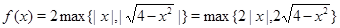 
.
Искомый график изображен на рисунке (см. рис.).
Пример Найдите масимальное значение выражения
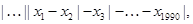
где 
, 
,..., 
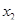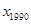--- различные натуральные числа от 1 до 1990.
Решение. Заметим, что модуль разности двух неотрицательных чисел не больше их максимума. Поэтому 
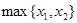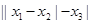не больше, чем 
, 
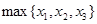не больше, чем 
, 
не больше, чем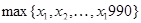 
. Далее, данное выражение не может равняться 1990, поскольку четность этого выражения совпадает с четностью суммы 
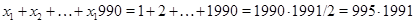. Наконец приведем пример, показывающий, что значение выражения может равняться 1989:
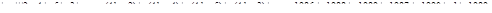
Ответ. 1989.
|
|
|
