 |
Типовые тестовые задачи, содержащие переменную под знаком модуля
|
|
|
|
Пример Найти корни уравнения  .
.
Решение. Так как  , то из уравнения следует, что
, то из уравнения следует, что  ,
,  . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид:  ,
,  . Корни этого уравнения
. Корни этого уравнения  ,
,  . Корень
. Корень  , поэтому он не является решением, а
, поэтому он не является решением, а  .
.
Ответ.  .
.
Пример Найти произведение корней уранения  .
.
Решение. Обозначим  ,
,  . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид: 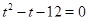 . Корни этого уравнения
. Корни этого уравнения  ,
,  . Так как
. Так как  , то
, то  . Отсюда
. Отсюда  ,
,  . Произведение корней равно
. Произведение корней равно  .
.
Ответ.  .
.
Пример Найти разность между наибольшими и наименьшим корнями уравнения 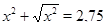 .
.
Решение. Обозначим  ,
,  . Тогда исходное уравнение примет вид:
. Тогда исходное уравнение примет вид:  . Решим его. Корни этого уравнения
. Решим его. Корни этого уравнения  ,
,  . Так как
. Так как  , то значение
, то значение  не подходит. Поэтому
не подходит. Поэтому  . Разность между наибольшим и наименьшим корнями уравнения равна
. Разность между наибольшим и наименьшим корнями уравнения равна  .
.
Ответ.  .
.
Пример Найти сумму корней уравнения  .
.
Решение. Используем правило:  . Исходное уравнение запишем в виде совокупности уравнений:
. Исходное уравнение запишем в виде совокупности уравнений:  Таким образом сумма корней исходного уравнения равна
Таким образом сумма корней исходного уравнения равна  .
.
Другой путь. Поскольку обе части уравнения неотрицательны, возведем уравнение в квадрат. Получим:  ,
,  . Так как дискриминант уравнения положительный, то по теореме Виета сумма корней равна
. Так как дискриминант уравнения положительный, то по теореме Виета сумма корней равна 
Ответ.  .
.
Пример Сколько целых корней на отрезке  имеет уравнение
имеет уравнение

Решение. Рассмотрим квадратный трехчлен  . Так как
. Так как 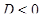 , то
, то  , поэтому исходное уравнение запишется как
, поэтому исходное уравнение запишется как


Последнее уравнение эквивалентно неравенству  , решение которого
, решение которого  . Таким образом, уравнение имеет 6 корней на отрезке
. Таким образом, уравнение имеет 6 корней на отрезке  :
:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Ответ. 6.
Пример Какое наибольшее конечное число корней может иметь уравнение

где  ,
,  ,...,
,...,  ,
, 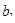 ,
,  ,...,
,...,  --- различные числа?
--- различные числа?
Решение. Положим  и перепишем исходное уравнение в виде
и перепишем исходное уравнение в виде 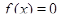 .
.
Пусть  --- все числа из множества
--- все числа из множества  , упорядоченные по возрастанию. На каждом из 101 промежутка
, упорядоченные по возрастанию. На каждом из 101 промежутка  ,
,  ,...,
,...,  ,
,  , функция
, функция  линейна. Заметим, что на первом и последнем из этих промежутков
линейна. Заметим, что на первом и последнем из этих промежутков  и
и  соответственно, при этом
соответственно, при этом  , так как количество корней конечно.
, так как количество корней конечно.
|
|
|
Пойдем по числовой оси слева направо.
Вначале угловой коэффициент функции  равен 0. Всякий раз, когда мы проходим одну из точек
равен 0. Всякий раз, когда мы проходим одну из точек  , он за счет смены знака при раскрытии соответствующего модуля изменяется на
, он за счет смены знака при раскрытии соответствующего модуля изменяется на 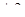 .
.
Таким образом, он всегда равен четному целому числу и не может поменять знак, не обратившись перед этим в 0.
Значит, угловые коэффициенты на любых двух соседних промежутках либо оба неотрицательны, либо оба неположительны, т.е. функция  на объединении этих промежутков либо неубывающая, либо невозрастающая.
на объединении этих промежутков либо неубывающая, либо невозрастающая.
Стало быть, если число ее корней конечно, то на каждом из 50 промежутков  ,...,
,...,  ,
,  она имеет не более одного корня. Кроме того, на крайних интервалах значения имеют разные знаки, и в каждом корне знак функции меняется. Следовательно, количество корней нечетно и не превышает 49.
она имеет не более одного корня. Кроме того, на крайних интервалах значения имеют разные знаки, и в каждом корне знак функции меняется. Следовательно, количество корней нечетно и не превышает 49.
Нетрудно проверить, что если роль  будут играть числа 1, 4, 5, 8, 97, 100, а роль
будут играть числа 1, 4, 5, 8, 97, 100, а роль  --- числа 2, 3, 6, 7, 94, 95, 98,
--- числа 2, 3, 6, 7, 94, 95, 98, 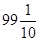 , то уравнение
, то уравнение  будет иметь ровно 49 корней.
будет иметь ровно 49 корней.
Ответ. 49.
Пример Решите систему неравенств

Решение. Предположим, что данная система неравенств имеет решение  ,
,  ,
,  ,
,  . Тогда, в частности,
. Тогда, в частности, 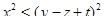 , т. е.
, т. е.

Аналогично получаем

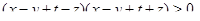

Перемножим все полученные неравенства. С одной стороны, произведение четырёх положительных чисел положительно. С другой стороны, это произведение равно ---

Приходим к противоречию.
Ответ. Система не имеет решений.
Пример Существуют ли действительные числа  ,
,  и
и 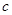 такие, что при всех действительных
такие, что при всех действительных  и
и  выполняется неравенство
выполняется неравенство

Решение. Предположим, что такие числа  ,
,  и
и 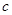 существуют. Выберем
существуют. Выберем  и
и  такие, что
такие, что  ,
,  ,
,  . Тогда разность между левой и правой частями равна
. Тогда разность между левой и правой частями равна  . А если взять
. А если взять  и
и  такие, что
такие, что  ,
,  ,
,  , то эта разность будет равна
, то эта разность будет равна  . Таким образом, с одной стороны,
. Таким образом, с одной стороны,  , с другой
, с другой  . Противоречие.
. Противоречие.
|
|
|
Ответ. Нет.
Пример Сколько различных целочисленных решений имеет неравенство 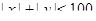 ?
?
Решение. При натуральном  уравнение
уравнение 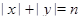 имеет ровно
имеет ровно  целочисленных решений, а при
целочисленных решений, а при  решение единственно. Таким образом, количество решений исходного неравенства равно
решение единственно. Таким образом, количество решений исходного неравенства равно  .
.
Ответ. 19801.
Пример Найдите все значения параметра  , при каждом из которых уравнение имеет три различных корня; найдите эти корни:
, при каждом из которых уравнение имеет три различных корня; найдите эти корни:  .
.
Решение. Возведем обе части уравнения в квадрат:  .
.
Если  , тогда получим уравнение:
, тогда получим уравнение:

Дискриминант этого уравнения равен:
 .
.
Уравнение (1) будет иметь один корень, при  и
и  . Два корня, при
. Два корня, при  и
и  .
.
Если  , тогда получим уравнение:
, тогда получим уравнение:

Дискриминант этого уравнения равен:
 .
.
Уравнение (2) будет иметь один корень при  и
и  . Два корня --- при
. Два корня --- при  и
и  .
.
Делаем вывод, что при  уравнение (1) имеет один корень, а уравнение (2) --- два корня. При
уравнение (1) имеет один корень, а уравнение (2) --- два корня. При  , уравнение (1) имеет два корня, а уравнение (2) --- один.
, уравнение (1) имеет два корня, а уравнение (2) --- один.
Таким образом, при  и
и  данное уравнение имеет три корня.
данное уравнение имеет три корня.
Найдем эти корни. При  , первое уравнение примет вид:
, первое уравнение примет вид:  . Оно имеет один корень:
. Оно имеет один корень: 
Уравнение (2) примет вид:  которое имеет два корня:
которое имеет два корня:  ,
,  .
.
При  , уравнение (2) примет вид:
, уравнение (2) примет вид:  . Оно имеет один корень:
. Оно имеет один корень:  .
.
Уравнение (1) при этом станет: 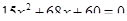 , которое будет иметь корни:
, которое будет иметь корни: 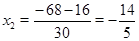 ,
,  .
.
Ответ. При  ,
,  ,
,  ,
,  .
.
При  ,
,  ,
,  ,
,  .
.
Пример Для каждого значения параметра  определите число решений уравнения
определите число решений уравнения  .
.
Решение.
1. Если  , тогда уравнение не имеет решений, модуль любого вещественного числа неотрицателен.
, тогда уравнение не имеет решений, модуль любого вещественного числа неотрицателен.
2. Если  , тогда получим уравнение
, тогда получим уравнение  . Это уравнение имеет два корня, так как
. Это уравнение имеет два корня, так как  .
.
3. Если  , тогда получаем совокупность двух уравнений:
, тогда получаем совокупность двух уравнений:

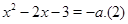
Первое уравнение имеет дискриминант:  . Оно не будет иметь корней при
. Оно не будет иметь корней при  ,
,  , но это невозможно, так как
, но это невозможно, так как  . Также оно не может иметь один корень (тогда
. Также оно не может иметь один корень (тогда  , что также невозможно). Таким образом, при
, что также невозможно). Таким образом, при  уравнение (1) имеет два корня.
уравнение (1) имеет два корня.
Второе уравнение имеет дискриминант:
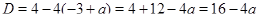 . Оно не будет иметь корней, если
. Оно не будет иметь корней, если  ,
,  ,
,  . Будет иметь один корень, если
. Будет иметь один корень, если  . Будет иметь два корня, если
. Будет иметь два корня, если  .
.
Окончательно получаем.
Ответ. Если  , тогда уравнение не имеет корней.
, тогда уравнение не имеет корней.
Если  и
и  , тогда уравнение имеет два корня.
, тогда уравнение имеет два корня.
Если  , тогда уравнение имеет три корня.
, тогда уравнение имеет три корня.
Если  , тогда уравнение имеет четыре корня.
, тогда уравнение имеет четыре корня.
Пример Найдите все значения параметра  из промежутка
из промежутка  , при каждом из которых больший из корней уравнения
, при каждом из которых больший из корней уравнения  принимает наибольшее значение.
принимает наибольшее значение.
|
|
|
Решение.
Преобразуем уравнение к виду 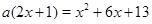 .
.
Значит, если  ,
,  , тогда
, тогда  . Найдем наибольшее значение
. Найдем наибольшее значение  , при котором
, при котором 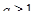 , т. е. наибольшее решение неравенства
, т. е. наибольшее решение неравенства  .
.
Преобразуем это неравенство:  ,
,  ,
,  ,
,  ,
,  .
.
Последнее неравенство решим методом интервалов, помня, что  .
.
Решение неравенства будет множество: 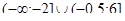 .
.
Ясно, что дробь  принимает наибольшее значение при
принимает наибольшее значение при  , тогда значение
, тогда значение  будет равно:
будет равно:  .
.
Ответ. При  .
.
Пример Найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  имеет единственное решение.
имеет единственное решение.
Решение.
Найдем решения для каждого значения  , а затем отберем те, которые удовлетворяют условию задачи, т. е. при которых уравнение имеет единственное решение.
, а затем отберем те, которые удовлетворяют условию задачи, т. е. при которых уравнение имеет единственное решение.
Для каждого фиксированного  будем искать решения данного уравнения сначала на промежутке
будем искать решения данного уравнения сначала на промежутке  , а потом на промежутке
, а потом на промежутке 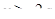 , поскольку модуль обращается в нуль при
, поскольку модуль обращается в нуль при  :
:
1) Пусть  . На этом промежутке
. На этом промежутке 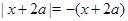 и поэтому данное уравнение примет вид
и поэтому данное уравнение примет вид  .
.
Найдем дискриминант полученного приведенного квадратного уравнения
 , значит, при любом действительном значении
, значит, при любом действительном значении  уравнение имеет два различных действительных корня:
уравнение имеет два различных действительных корня:  и
и 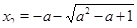 .
.
Выясним, входят ли они в промежуток 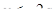 . Корень
. Корень  лежит в этой области только тогда, когда выполняется неравенство:
лежит в этой области только тогда, когда выполняется неравенство:  или
или  .
.
Последнее неравенство равносильно системе неравенств:

Последняя система неравенств не имеет решений, значит, ни при каком значении параметра a число  не лежит в области
не лежит в области  .
.
Корень  лежит в рассматриваемой области тогда, когда выполнено неравенство:
лежит в рассматриваемой области тогда, когда выполнено неравенство:  или
или  .
.
Решим последнее неравенство. Ясно, что этому неравенству удовлетворяют все значения  из промежутка
из промежутка  .
.
При  получим неравенство
получим неравенство  . Отсюда находим:
. Отсюда находим:  .
.
Таким образом, при 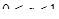 уравнение имеет единственное решение
уравнение имеет единственное решение 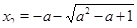 .
.
2) Пусть  . На этом промежутке
. На этом промежутке 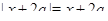 и поэтому исходное уравнение можно переписать в виде
и поэтому исходное уравнение можно переписать в виде  . Найдем дискриминант этого уравнения:
. Найдем дискриминант этого уравнения:  .
.
Уравнение не имеет решений, если  , т. е. если
, т. е. если  .
.
Значит, уравнение не имеет корней для  из промежутка
из промежутка  .
.
|
|
|
Если  не принадлежат этому промежутку, то квадратное уравнение имеет корни
не принадлежат этому промежутку, то квадратное уравнение имеет корни  ,
,  , причем
, причем  при
при  и
и  . Выясним теперь, при каких значениях параметра
. Выясним теперь, при каких значениях параметра  найденные корни лежат в области
найденные корни лежат в области  .
.
Для этого нужно решить неравенства  и
и  .
.
Неравенство 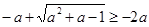 равносильно неравенству
равносильно неравенству  или совокупности двух систем неравенств:
или совокупности двух систем неравенств:

Множество решений первой системы имеет вид  , вторая система не имеет решений. Значит, только при значении
, вторая система не имеет решений. Значит, только при значении  корень уравнения
корень уравнения  лежит в области
лежит в области 
Неравенство  равносильно неравенству
равносильно неравенству  или системе неравенств
или системе неравенств

Множество решений полученной системы неравенств есть отрезок  .
.
Только при этих значениях параметра  , корень
, корень  принадлежит области:
принадлежит области:  . Таким образом, при
. Таким образом, при 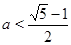 данное уравнение в области
данное уравнение в области  решений не имеет.
решений не имеет.
Если  , то уравнение в рассматриваемой области имеет единственное решение
, то уравнение в рассматриваемой области имеет единственное решение  .
.
При значениях  , лежащих в области
, лежащих в области  исходное уравнение имеет два различных корня
исходное уравнение имеет два различных корня  и
и  . Если же
. Если же  , то исходное уравнение имеет единственный корень
, то исходное уравнение имеет единственный корень  . Полученные результаты удобно свести в таблицу:
. Полученные результаты удобно свести в таблицу:

Таким образом, искомые значения  образуют два промежутка:
образуют два промежутка: 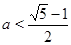 и
и  .
.
Ответ. 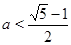 ,
,  .
.
Пример Найти все корни уравнения 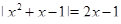 , удовлетворяющее неравенству
, удовлетворяющее неравенству  .
.
Решение. Строим графики функций  и
и  . Получим две точки пересечения, абсцисса только одной из них меньше
. Получим две точки пересечения, абсцисса только одной из них меньше  , т. е. удовлетворяет условию задачи (см. рис.).
, т. е. удовлетворяет условию задачи (см. рис.).
pics/ex14.eps
Абсциссу точки можно получить решив уравнение  .
.
Ответ.  .
.
Пример Решить аналитически и графически уравнение

Аналитическое решение
Преобразуем уравнение, умножив обе его части на 2, будучи положительным числом, его можно вносить под знак модуля, поэтому получим:

У каждого из трехчленов положительные дискриминанты. Это дает возможность разложить каждый из них на линейные множители.
Уравнение примет вид:  .
.
На числовой прямой отложим точки, в которых каждый из множителей обращается в нуль. В результате получим пять промежутков, на каждом из которых определим знаки трехчленов под модулем и решим полученные уравнения.
Однако такой способ не будет рациональным. Целесообразнее изобразить промежутки знакопостоянства каждого из трехчленов на числовых осях. Тогда определение их знаков будет упрощено и сделается более наглядным (см. рис.).
pics/ex9.eps
При таком схематическом изображении понятно, что:
1) при  оба трехчлена положительны и уравнение примет вид:
оба трехчлена положительны и уравнение примет вид:

Решая его, находим  ,
,  . Оба корня не входят в промежуток
. Оба корня не входят в промежуток  и являются посторонними;
и являются посторонними;
2) при  первый трехчлен отрицателен, а второй положителен, получим уравнение:
первый трехчлен отрицателен, а второй положителен, получим уравнение:  откуда находим корень
откуда находим корень  , который входит в промежуток
, который входит в промежуток  и является решением уравнения;
и является решением уравнения;
3) при  оба трехчлена отрицательны, получаем:
оба трехчлена отрицательны, получаем:
|
|
|
 , откуда
, откуда  , который входит в промежуток
, который входит в промежуток  и является решением уравнения;
и является решением уравнения;
4) при  первый трехчлен положителен, второй --- отрицателен, получаем уравнение:
первый трехчлен положителен, второй --- отрицателен, получаем уравнение:
 , отсюда
, отсюда 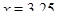 , который входит в промежуток
, который входит в промежуток  и является решением уравнения;
и является решением уравнения;
5) при  оба трехчлена положительны, получается такая же ситуация, как и в первом случае. И здесь, оба корня
оба трехчлена положительны, получается такая же ситуация, как и в первом случае. И здесь, оба корня  ,
,  не входят в промежуток и являются посторонними.
не входят в промежуток и являются посторонними.
Ответ.  ,
,  ,
,  .
.
Графическое решение
Для графического решения преобразуем уравнение:


Построим графики функций  и
и 
График функции  будем строить в несколько этапов:
будем строить в несколько этапов:
а) строим график функции  ;
;
б) строим график функции  , ``зеркально'' отразив нижнюю часть кривой
, ``зеркально'' отразив нижнюю часть кривой  в оси
в оси 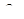 ;
;
в) строим график функции  для этого достаточно график функции
для этого достаточно график функции  ``опустить'' вниз (осуществить параллельный перенос вдоль оси
``опустить'' вниз (осуществить параллельный перенос вдоль оси  ) на
) на 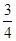 ;
;
г) полученный график полностью симметрично отразим в оси  , ``перевернем'' вокруг оси
, ``перевернем'' вокруг оси 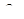 на
на  .
.
В результате получим график функции  .
.
График функции  построим уже известным способом: строим параболу
построим уже известным способом: строим параболу  и зеркально отражаем в оси
и зеркально отражаем в оси  только часть параболы, находящуюся ниже оси
только часть параболы, находящуюся ниже оси  .
.
Находим абсциссы точек пересечения графиков, которые и будут являться решениями уравнения (см. рис.).
pics/ex10.eps
Абсциссы точек пересечения следующие: 1,75; 2,5 и 3,25. Они и будут решениями уравнения.
Пример Решите уравнение 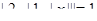 .
.
Решение. Решать будем это уравнение последовательно ``раскрывая'' модули, начиная с ``внешнего'' и ``приближаясь'' к переменной  .
.
После раскрытия первого модуля, получим совокупность двух уравнений:
(1)  или (2)
или (2)  .
.
Решая уравнение (1), в свою очередь, получаем два уравнения:
 ,
,
(3)  или (4)
или (4)  .
.
Из уравнения (3) находим: 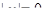 ,
, 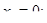 из уравнения (4) находим:
из уравнения (4) находим: 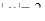 ,
, 
Решая уравнение (2), также получим:  , которое распадается два уравнения:
, которое распадается два уравнения:
(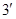 )
)  или (
или ( )
)  .
.
Из (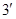 ) получаем:
) получаем:  ,
,  ,
,  Из (
Из ( )
)  , которое не имеет решений.
, которое не имеет решений.
Ответ. 
Пример Решить уравнение:

Решение. ОДЗ данного уравнения:

Простой проверкой нетрудно убедиться, что  и
и  --- решения данного уравнения.
--- решения данного уравнения.
Ответ.  .
.
Если решать уравнение путем возведения в квадраты обеих его частей, то получится уравнение

У этого уравнения добавится ``лишний'' корень  , не принадлежащий ОДЗ.
, не принадлежащий ОДЗ.
Преобразование  , не равносильное, т.к.
, не равносильное, т.к.  входит в ОДЗ исходного выражения, но не входит в ОДЗ преобразованного.
входит в ОДЗ исходного выражения, но не входит в ОДЗ преобразованного.
Нюанс состоит в том, что при  функция
функция  существует и при
существует и при  , т.к. на что ноль ни умножай --- будет ноль.
, т.к. на что ноль ни умножай --- будет ноль.
Пример Решить уравнение  .
.
Решение. Начнем раскрывать внутренний модуль (раскрытие внешнего модуля займет гораздо больше времени):
1. При  имеем
имеем  .
.
Теперь рассмотрим два случая:
а)  , т.е.
, т.е.  ;
;
б)  и
и 
Т.к. функция, стоящая в первой части исходного уравнения, --- четная, то решением так же будет  и
и  .
.
Ответ.  .
.
Пример Чему равна сумма корней уравнения (корень, если он один) уравнения
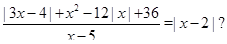
Решение. Рассмотрим выражение

и преобразуем его к виду

Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если  (т.к.
(т.к.  ). Преобразуем полученное выражение, при условии
). Преобразуем полученное выражение, при условии  . Получим уравнение, равносильное исходному:
. Получим уравнение, равносильное исходному:


Ответ.  .
.
Пример Все значения квадратного трёхчлена  на отрезке
на отрезке  по модулю не превосходят 1. Какое наибольшее значение при этом может иметь величина
по модулю не превосходят 1. Какое наибольшее значение при этом может иметь величина  ?
?
Ответ. Максимальное значение величины  равно 17.
равно 17.
Докажем это. Сначала докажем, что эта величина не может быть больше 17. Так как значения трёхчлена 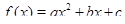 на отрезке
на отрезке 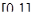 по модулю не превосходят единицы, то
по модулю не превосходят единицы, то  ,
,  ,
,  , то есть
, то есть  ,
,  ,
,  . Так как модуль суммы не превосходит суммы модулей, то
. Так как модуль суммы не превосходит суммы модулей, то



