Аналогично находим ускорение

Билет№16

Векторный способ задания движения точки

Положение движущейся точки определено в любой момент времени радиусом-вектором , проведенным из точки , неподвижной относительно выбранной системы отсчета (рис. 10.1).

При движении точки 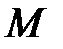ее радиус-вектор непрерывно изменяется, являясь функцией времени:

.

Это уравнение называется векторным уравнением движения точки.

Рис. 10.1

Если точку принять за начало прямоугольной системы отсчета и разложить радиус-вектор 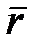по осям координат, то можно написать

,

 

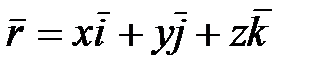где - проекции радиуса-вектора на координатные оси, равные координатам движущейся точки : 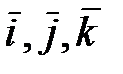- орты координатных осей.

Зная уравнения движения точки М вдоль координатных осей:

, , ,

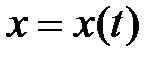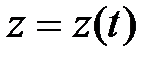можно для любого момента времени 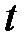построить ее радиус-вектор.

Таким образом, задание одного векторного уравнения равносильно заданию трех скалярных уравнений. Поэтому такой способ определения движения точки оказывается весьма удобным для доказательства теорем и установления общих зависимостей.

При решении задач, когда требуется получить численные результаты, применяют другие способы задания движения точки.

Cкоростью точки называется вектор, определяющий в каждый момент времени быстроту и направление движения. При этом, если в равные промежутки времени точка проходит одинаковые расстояния, то движение называется равномерным. В остальных случаях движение называется неравномерным.

Рис. 10.2

Размерность скорости , или 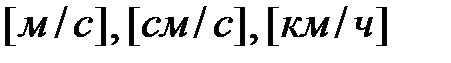и т.д.

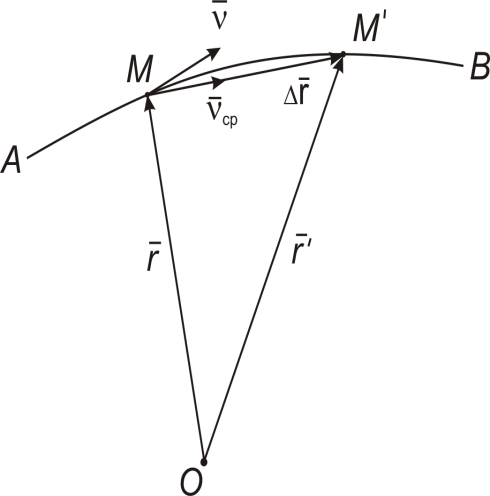
Рассмотрим случай криволинейного движения точки (рис. 10.2).

Рис. 10.2

Рис. 10.2

Из построений видно, что , откуда 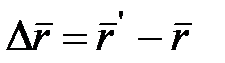, то есть вектор равен приращению радиуса-вектора : .

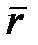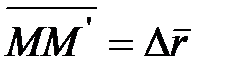Средняя скорость за время

.

Рис. 1.2

Истинная скорость точки в данный момент времени равна пределу вектора ее средней скорости при :

 

,

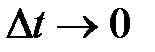то есть 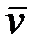точки равна первой производной ее радиуса-вектора по времени. При 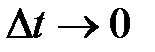секущая 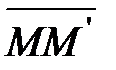стремится стать касательной. Следовательно, вектор скорости 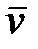всегда направлен по касательной к траектории.

Ускорение– это величина, характеризующая быстроту изменения скорости по модулю и направлению.

Из рис. 10.4 видно

.

 

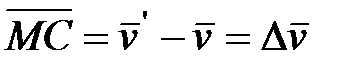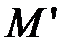
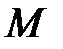
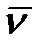
А

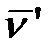
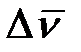
Е

Рис. 10.4

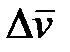Вектор , являющийся геометрической разностью векторов скорости точки в конце и начале данного промежутка времен 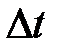, называется приращением скорости точки за соответствующий промежуток времени.

Среднее ускорение точки в течение этого времени

.

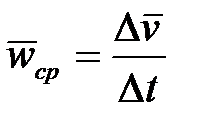Истинное значение ускорения равно пределу этого отношения при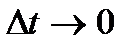

,

то есть ускорение точки равно первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Важно отметить, что модуль производной по времени от вектора скорости (модуль полного ускорения) не равен производной от модуля скорости : .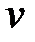

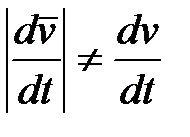Размерность ускорения 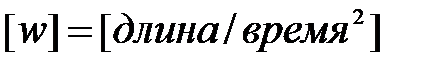, или .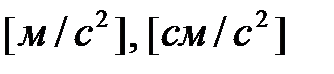

 

 

Билет№15

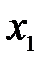
Рис. 10.3

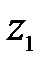
O

Годографом скорости называется геометрическое место концов векторов скорости в различные моменты времени, если их начала совместить в одной точке. Это понятие широко используется при исследовании полета снарядов в артиллерии, ракетной технике и т. д.

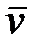
Если движение точки задано координатным способом (рис. 10.3): ,

,

,

 

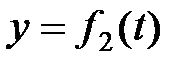то уравнения, описывающие годограф скорости, выглядят так:

,

,

.

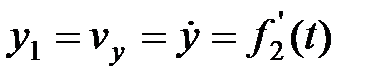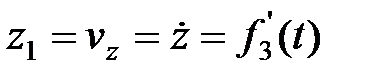При равномерном движении годограф является кривой, расположенной на сфере радиуса 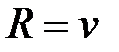, а для равномерного прямолинейного движения является точкой. При неравномерном прямолинейном движении он является прямой, параллельной траектории.

 

 

Билет№14

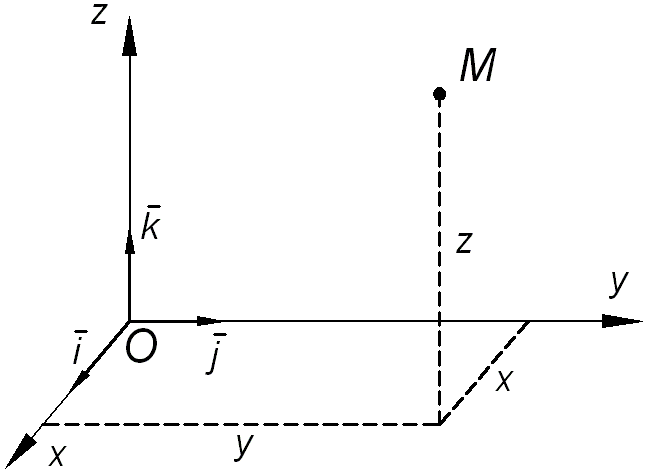Координатный способ заданиядвижения точки

Положение точки в каждый момент времени можно определить, если известны уравнения движения в декартовых координатах (рис. 10.5):

,

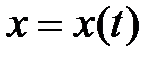Рис. 10.5

,

.

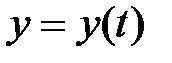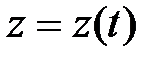Рис. 10.5

Уравнение траектории точки получается исключением параметра времени из этих выражений.

Можно написать

.

Рис. 10.5

Тогда . (10.1)

 

С другой стороны, 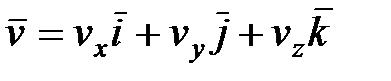, (10.2)

где - проекции вектора скорости на координатные оси.

Из сравнения равенств (10.1) и (10.2) вытекает

, , .

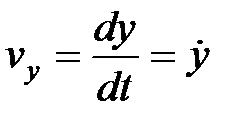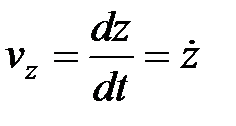Проекция скорости на какую-либо координатную ось равна первой производной от соответствующей координаты по времени.

Модуль вектора скорости .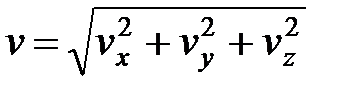

Направляющие косинусы

; ; .

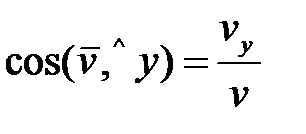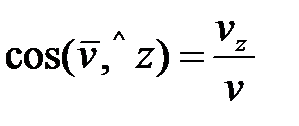Аналогично находим ускорение

.

 

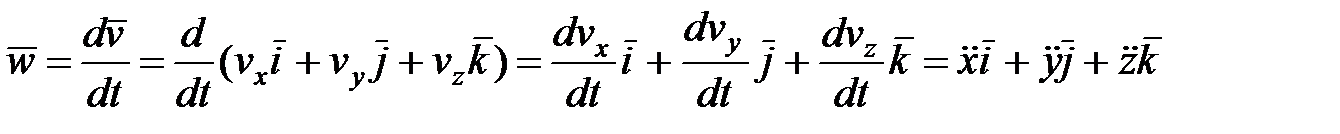С другой стороны, ,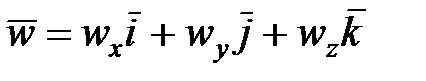

где 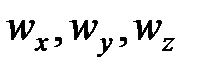- проекции вектора скорости на координатные оси.

Следовательно,

, , .

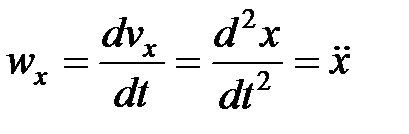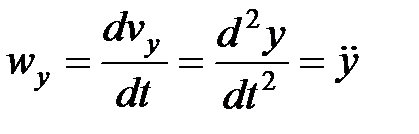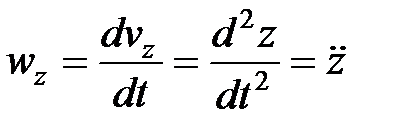Проекция ускорения точки на какую-либо координатную ось равна первой производной от проекции ее скорости на эту ось или второй производной от соответствующей координаты по времени.

Модуль вектора ускорения .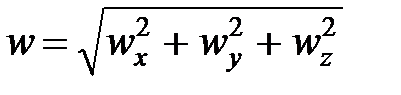

Направляющие косинусы ; ; .

 

 

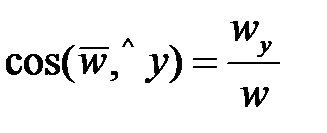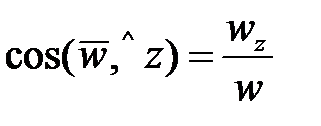Билет№13

А

В

M

O

M'

s

Δs

Рис. 11.1

Естественный способ задания

Движения точки

 

При естественном способе задания движения точки известны траектория , уравнение движения по этой траектории 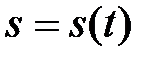, где - путь точки, начало и направление отсчета расстояний (рис. 11.1).

Пусть точка за время 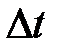из положения 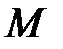переместилась в положение , пройдя дугу .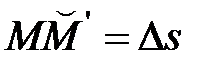

Средняя скорость за этот промежуток времени

,

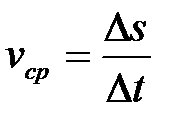истинная скорость в момент

.

 

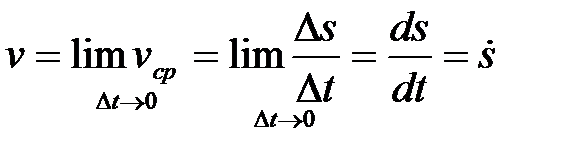При этом, если точка движется в сторону возрастания пути, то 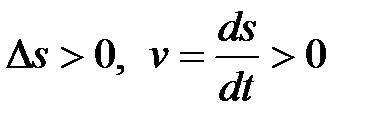(скорость положительна), а если в противоположную, то 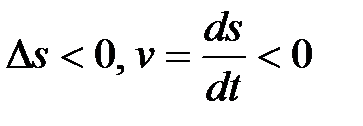(скорость отрицательна). То есть алгебраическая величина определяет не только модуль, но и направление скорости точки вдоль траектории.

Если величина 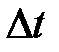столь мала, что изменением направления скорости можно пренебречь, то 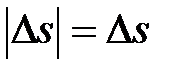. Тогда

,

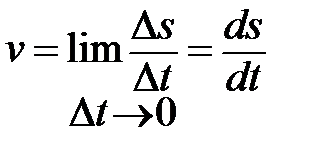Следовательно, .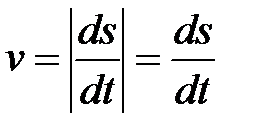

Модуль скорости равен модулю первой производной пройденного пути по времени.

Вектор скорости 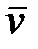всегда направлен по касательной к траектории.

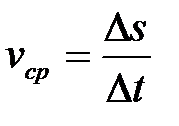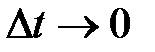
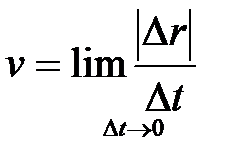Отметим, что величина средней скорости не равна модулю вектора средней скорости . Но в пределе при и 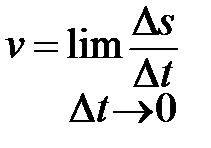равны между собой, так как .

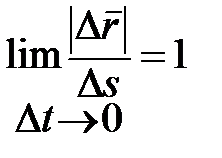В естественном способе задания движения точки ускорение 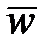раскладывается на составляющие вдоль естественных осей координат (рис. 11.2). Поясним рисунок.

Соприкасающаяся плоскость – плоскость, которая образована касательной к кривой в данной точке и другой точкой, бесконечно близкой к точке . Если кривая плоская, то она лежит в соприкасающейся плоскости.

Нормальная плоскость – плоскость, перпендикулярная к касательной. Любая прямая в ней является нормалью к кривой в точке.

Главная нормаль (в дальнейшем просто нормаль) – линия пересечения соприкасающейся и нормальной плоскостей, а прямая 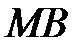- бинормаль.

Естественные оси координат – это совокупность трех взаимно перпендикулярных осей, начало которых совпадает в каждый момент времени с положением движущейся точки .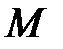

Ось 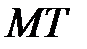направлена по касательной в сторону возрастания расстояний 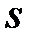, ось направлена по главной нормали в сторону вогнутости траектории, ось 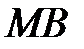направлена по бинормали так, чтобы она образовывала с первыми двумя осями правую систему координат.

B

T

N

O

Касательная плоскость

Нормальная плоскость

Соприкасающаяся плоскость

Бинормаль

Касательная

Главная нормаль

М

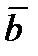
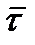
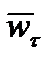
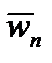
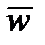
Рис. 11.2

Рис. 11.2

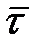Единичные векторы (орты) в естественных осях следующие: (вдоль касательной), 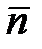(вдоль нормали), 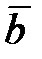(вдоль бинормали).

Тогда вектор ускорения через проекции на соответствующие оси выражается в виде

 

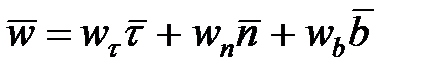. (11.1)

 

С другой стороны, вектор скорости всегда направлен по касательной, так что

 

.

 

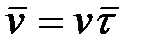Тогда

 

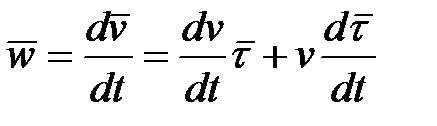. (11.2)

 

 

Рис. 11.3

Рассмотрим производную по времени от орта касательной .

Определим ее модуль. Построим параллелограмм (рис.11.3).Очевидно, , откуда .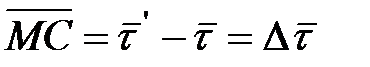

Обозначим 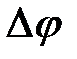- угол смежности, тогда

 

,

так как .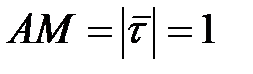

Находим модуль производной орта по времени

 

.

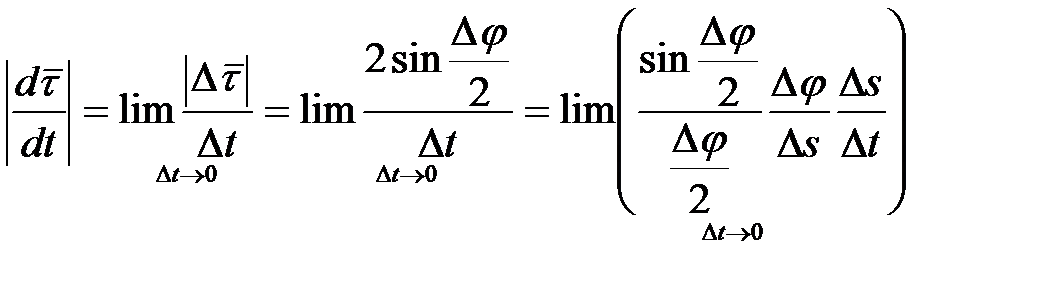При 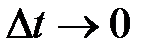также 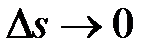, 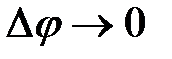. Тогда

 

,

 

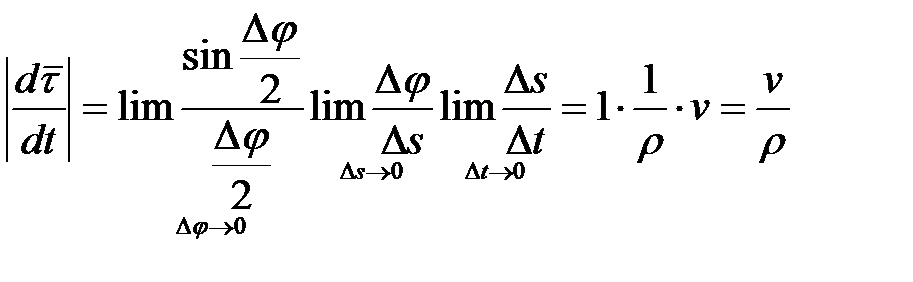где 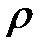- радиус кривизны.

Найдем предельное значение угла между векторами и при 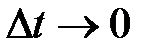. Напишем

.

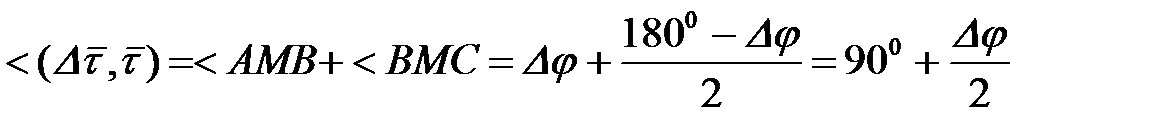Следовательно,

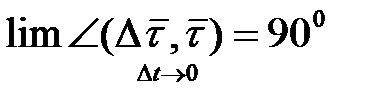, так как 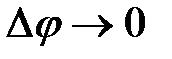при .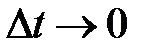

Из сказанного следует, что вектор лежит в соприкасающейся плоскости и направлен перпендикулярно к касательной вдоль нормали к траектории в точке , то есть его направление совпадает с направлением орта

.

Тогда на основании выражения (11.2)

. (11.3)

Сравнивая выражения (11.1) и (11.3), имеем:

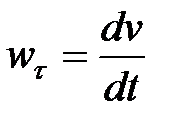- проекция ускорения точки на касательную (касательное ускорение) равна первой производной модуля скорости по времени. Оно характеризует изменение скорости по величине;

- проекция ускорения точки на главную нормаль (нормальное ускорение) равна квадрату скорости, деленному на радиус кривизны траектории. Оно характеризует изменение скорости по направлению;

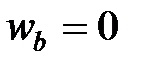- проекция ускорения точки на бинормаль касательную (бинормальное ускорение) равна нулю.

Таким образом, вектор ускорения лежит в соприкасающейся плоскости.

Нормальное ускорение положительно, так как всегда направлено по радиусу кривизны в сторону вогнутости траектории, то есть к центру кривизны.

Если касательное ускорение больше нуля (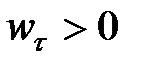), оно направлено в сторону положительной касательной (по направлению 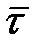), если меньше нуля (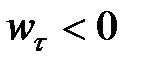) – в противоположную сторону.

Есл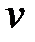и и 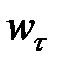имеют одинаковые знаки, то движение ускоренное, если разные, то оно замедленное.

Модуль полного ускорения

.

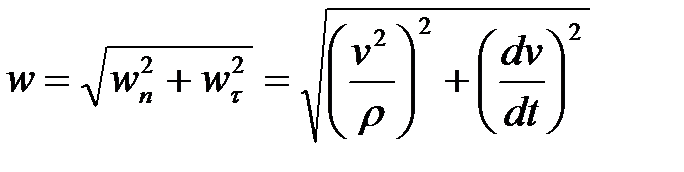Направляющие косинусы

 

; .

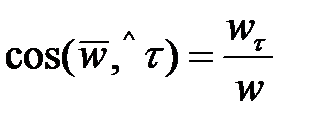123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: