Мгновенная ось вращения. Аксоиды

Ось, вокруг которой следует тело вращать для перевода его из одного положения в другое, бесконечно близкое к первому, называется мгновенной осью вращения (МОВ), или мгновенной осью (МО), для данного момента времени.

Любое движение тела вокруг неподвижной точки можно заменить последовательностью вращений вокруг совокупности мгновенных осей. Геометрическое место мгновенных осей относительно неподвижной системы координат называется неподвижным аксоидом. Он является конической поверхностью с вершиной в неподвижной точке, так как через нее проходят все МО.

Геометрическое место положений МО в подвижной системе координат называется подвижным аксоидом.

Для каждого движения твердого тела вокруг неподвижной точки имеется пара аксоидов, причем движение можно точно воспроизводить путем качения без скольжения подвижного аксоида по неподвижному, так как общая образующая этих аксоидов является в каждый момент времени мгновенной осью, вокруг которой вращается тело. Все ее точки неподвижны.

 

Векторы угловой скорости и углового ускорения

Как сказано выше, движение тела с одной неподвижной точкой можно рассматривать как совокупность вращений вокруг мгновенных осей. Для характеристики этого движения можно ввести понятия угловой скорости и углового ускорения .

ω

Угловая скорость является вектором, направленным вдоль мгновенной оси так, чтобы, глядя с его конца, можно было видеть вращение против часовой стрелки (рис. 15.3).

О

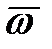Модуль вектора можно выразить через элементарный угол поворота вокруг МО за время :

 

Рис. 15.3

.

 

Таким образом, вектор характеризует величину угловой скорости вращения вокруг МО и направление вращения. Вектор - скользящий вектор.

Вектор углового ускорения при вращении тела вокруг неподвижной точки характеризует изменение вектора угловой скорости в данный момент по величине и направлению. Он является производной по времени от вектора угловой скорости :

.

 

В общем случае вектор не направлен по МО, а направлен параллельно касательной к годографу вектора вдоль прямой, проходящей через неподвижную точку О (вектор скользящий).

 

Билет№2

Скорость точки

При сферическом движении тело в каждый момент времени вращается вокруг мгновенной оси вращения, проходящей через закрепленную точку, с угловой скоростью , направленной по мгновенной оси. Точки тела, лежащие на МО, имеют скорости, равные нулю, как в случае неподвижной оси вращения.

Поэтому скорости точек тела при вращении вокруг неподвижной точки можно вычислить по векторной формуле Эйлера, как в случае неподвижной оси вращения, только радиус-вектор здесь удобнее проводить из неподвижной точки (хотя можно и из любой точки, лежащей на МО).

По векторной формуле Эйлера вектор скорости точки

, (16.1)

 

где - мгновенная угловая скорость вращения вокруг МО, - радиус-вектор точки М, проведенный из неподвижной точки О (рис. 16.1).

Модуль скорости ,

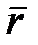
М

ω

где h - кратчайшее расстояние от точки М до МО.

Рис. 16.1

Таким образом, скорости точек тела пропорциональны расстояниям от них до мгновенной оси. Направление скорости какой-либо точки тела перпендикулярно к плоскости, образованной векторами и 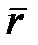, то есть перпендикулярно к отрезку . Следовательно, мгновенная угловая скорость вращения тела в данный момент времени может быть определена как отношение скорости точки к кратчайшему расстоянию от точки до МО.

Рис. 16.2

Нередко мгновенную ось находят из условий наложенных связей. Она всегда проходит через две неподвижные в данный момент точки тела. Так, например, если конус катится без скольжения по неровной поверхности (рис. 16.2), то МО проходит через неподвижную точку О и мгновенную точку контакта К. При известной скорости точки угловая скорость конуса

,

где - высота конуса, - половина угла при вершине конуса.

Проектируя соотношение (16.1) на координатные оси, получим формулы Эйлера для проекций вектора скорости на эти оси

,

, (16.2)

,

где - координаты точки, скорость которой определяется.

Для определения положения МО достаточно в соотношении (16.2) проекции скорости принять равными нулю

,

,

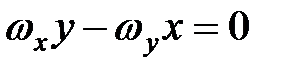,или . (16.3)

 

Если величины, входящие в выражение (16.3) рассматривать как функции времени, то получим уравнения подвижного или неподвижного аксоидов в параметрической форме в зависимости от того, в какой системе координат это выражение (16.3) составлено.

Учитывая, что , векторную формулу Эйлера можно написать так;

, (16.4)

то есть найдена производная по времени от вектора , постоянного по модулю.

 

Билет№1

Ускорение точки

Так как в общем случае сферического движения векторы углового ускорения 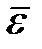и угловой скорости 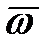тела не совпадают по направлению, как при неподвижной оси вращения, то известные формулы для ускорений точек здесь не применимы.

Используем формулу (16.1) для определения ускорения точки как производной вектора скорости по времени

.

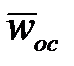
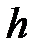
Так как , , то

. (16.5)

Выражение (16.5) называется формулой Ривальса.

Часть общего ускорения (рис. 16.3)

(16.6)

Рис. 16.3

называется вращательным ускорением, а другая часть

- (16.7)

осестремительным ускорением.

Тогда формула (16.5) имеет вид

, (16.8)

то есть ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного ускорений.

Эти векторы в общем случае не являются взаимно перпендикулярными, поэтому величину полного ускорения точки можно вычислить по теореме косинусов:

. (16.9)

Заметим, что формула (16.6) аналогична векторной формуле Эйлера (16.1). Поэтому вращательное ускорение можно определять как скорость точки при вращении тела с угловой скоростью .

Величина вращательного ускорения

, (16.10)

где - кратчайшее расстояние от точки тела до линии действия вектора .

Из выражения (16.10) следует, что вектор проходит через неподвижную точку, так как в ином случае эта точка имела бы вращательное ускорение, отличное от нуля.

Модуль осестремительного ускорения получим из формулы (16.7):

,

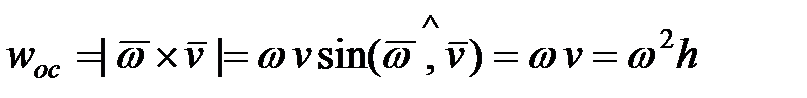так как .

Вектор 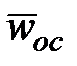направлен перпендикулярно к МО.

Если ввести вектор 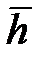, то

.

В случае вращения твердого тела вокруг неподвижной оси угловое ускорение и угловая скорость направлены по этой оси и тогда .

Таким образом, вращательное ускорение превращается в касательноеускорение, а осестремительное - в нормальное, или центростремительное, ускорение.

Следовательно, вращение тела вокруг неподвижной точки можно рассматривать как более общий случай по отношению к вращению тела вокруг неподвижной оси.

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: