Разложение плоского движения
Угол поворота и направление вращения фигуры не зависят от выбора полюса.
Рассмотрим перемещение тела за конечный промежуток времени (рис. 14.3).
Разбивая  на мелкие отрезки времени
на мелкие отрезки времени  , можно получить ряд промежуточных положений тела, очень близких друг к другу. Выбрав какую-либо точку А за полюс, можно фигуру перевести из заданного положения в соседнее путем поступательного перемещения тела вместе с полюсом и вращательного вокруг него.
, можно получить ряд промежуточных положений тела, очень близких друг к другу. Выбрав какую-либо точку А за полюс, можно фигуру перевести из заданного положения в соседнее путем поступательного перемещения тела вместе с полюсом и вращательного вокруг него.
Аналогично можно провести тело через все его положения. Таким образом, движение плоской фигуры можно разложить на два движения: поступательное вместе с полюсом и вращательное вокруг полюса.
По аналогии со сложным движением точки, поступательное движение относительно неподвижной системы координат можно представить как переносное движение фигуры вместе с полюсом, вращательное движение вокруг него как относительное, а результирующее движение относительно неподвижной системы как абсолютное движение. Переносное поступательное движение зависит от выбора полюса, а угол поворота тела в относительном вращении от полюса не зависит (угол  один и тот же при выборе полюса в точке А или В).
один и тот же при выборе полюса в точке А или В).
 Так как угол поворота
Так как угол поворота  не зависит от выбора полюса, то угловая скорость
не зависит от выбора полюса, то угловая скорость  и угловое ускорение
и угловое ускорение  также не зависят от выбора полюса.
также не зависят от выбора полюса.
Скорость точки. Угловая скорость тела
Метод полюса. На основании теоремы о сложении скоростей  можно написать
можно написать
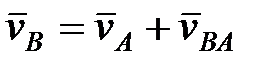 . (14.1)
. (14.1)
Скорость любой точки плоской фигуры в любой момент времени равна геометрической сумме скорости другой произвольно выбранной точки фигуры (полюса) и скорости вращения первой точки относительно второй. На рис. 14.4
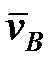
- скорость точки
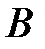
,
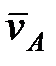
- скорость полюса
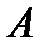
,
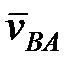
- скорость точки
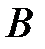
во вращении вокруг полюса

.
Справедливо векторное выражение
 ,
,
а по модулю  ,
,
откуда следует

.
Теорема о проекциях скоростей двух точек. Проекции векторов скоростей двух точек на прямую, их соединяющую, равны между собой.
Доказательство
Спроектируем равенство (14.1) на прямую 
 ,
,
где проекция  , так как вектор
, так как вектор 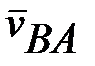 перпендикулярен к прямой
перпендикулярен к прямой  .
.
Следовательно,  , то есть теорема доказана.
, то есть теорема доказана.
Билет№6Начало в билете№8
За полюс может быть принята любая точка плоской фигуры.
В общем случае имеется такая точка фигуры, скорость которой в данный момент времени равна нулю.Это позволяет упростить изучение плоского движения тела.
На перпендикуляре к  отложим от точки
отложим от точки 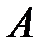 в сторону вращения
в сторону вращения  отрезок
отрезок  (рис. 14.5).
(рис. 14.5).
Тогда скорость точки 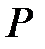
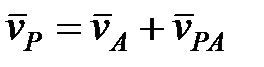
,
где
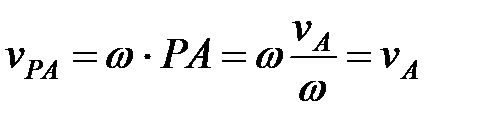
, а с другой стороны,
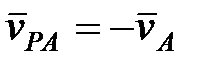
.
Следовательно, 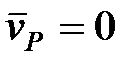 .
.
Точка  движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).
движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).
МЦС лежит на пересечении перпендикуляров к векторам скоростей точек, восстановленных из самих точек. Поэтому, зная векторы скоростей хотя бы двух точек, легко установить положение МЦС.
Можно написать (рис. 14.6)
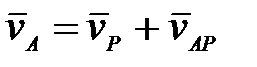
,
 ,
,
 ,
,
что с учетом  равносильно
равносильно
 ,
,  ,
,  .
.
Скорости точек пропорциональны их расстояниям до МЦС. Их векторы направлены перпендикулярно к отрезкам, соединяющим точки с МЦС. Это свойственно вращательному движению, и плоское движение можно рассматривать как совокупность мгновенных вращений вокруг МЦС.
Направление вращения тела определяется направлением вектора скорости точки.
Сказанное справедливо, когда векторы скоростей точек не параллельны друг другу.
Если векторы скоростей точек параллельны ( ||
||  ), этот прием не применим и возможны следующие случаи.
), этот прием не применим и возможны следующие случаи.
Случай 1 (рис. 14.7). Точки А, В не лежат на общем перпендикуляре к векторам их скоростей.
МЦС лежит в бесконечности, и угловая скорость равна нулю ( ). Тело совершает мгновенно поступательное движение.
). Тело совершает мгновенно поступательное движение.
Случай 2 (рис. 14.8). Точки
А, В лежат на общем перпендикуляре к векторам их скоростей.
Достаточно провести прямую через концы векторов скоростей точек, построенных в одном масштабе, и из подобия треугольников найти расстояние
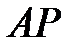
(или
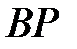
), определяющее положение точки
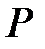
на прямой
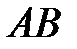
по формулам (с учетом знаков скоростей)
Билет7 Начало в билете№8
Воспользуйтесь поиском по сайту:


 на мелкие отрезки времени
на мелкие отрезки времени  , можно получить ряд промежуточных положений тела, очень близких друг к другу. Выбрав какую-либо точку А за полюс, можно фигуру перевести из заданного положения в соседнее путем поступательного перемещения тела вместе с полюсом и вращательного вокруг него.
, можно получить ряд промежуточных положений тела, очень близких друг к другу. Выбрав какую-либо точку А за полюс, можно фигуру перевести из заданного положения в соседнее путем поступательного перемещения тела вместе с полюсом и вращательного вокруг него. один и тот же при выборе полюса в точке А или В).
один и тот же при выборе полюса в точке А или В). Так как угол поворота
Так как угол поворота  не зависит от выбора полюса, то угловая скорость
не зависит от выбора полюса, то угловая скорость  и угловое ускорение
и угловое ускорение  также не зависят от выбора полюса.
также не зависят от выбора полюса. можно написать
можно написать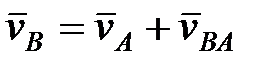 . (14.1)
. (14.1)




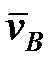 - скорость точки
- скорость точки 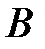 ,
, 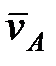 - скорость полюса
- скорость полюса 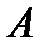 ,
, 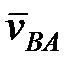 - скорость точки
- скорость точки 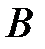 во вращении вокруг полюса
во вращении вокруг полюса  .
. ,
, ,
, .
.

 ,
, , так как вектор
, так как вектор 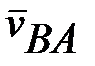 перпендикулярен к прямой
перпендикулярен к прямой  .
. , то есть теорема доказана.
, то есть теорема доказана.

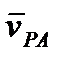
 отложим от точки
отложим от точки 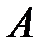 в сторону вращения
в сторону вращения  отрезок
отрезок  (рис. 14.5).
(рис. 14.5).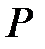
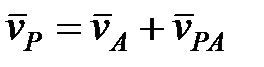 ,
,




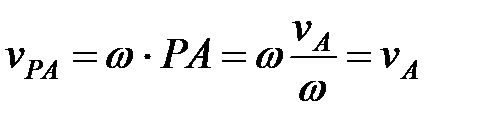 , а с другой стороны,
, а с другой стороны, 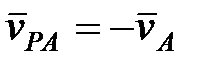 .
.
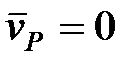 .
. движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).
движущейся плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей (МЦС).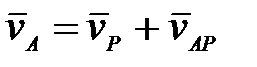 ,
,
 ,
, ,
, равносильно
равносильно ,
,  ,
,  .
.

 ||
||  ), этот прием не применим и возможны следующие случаи.
), этот прием не применим и возможны следующие случаи. ). Тело совершает мгновенно поступательное движение.
). Тело совершает мгновенно поступательное движение.


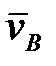
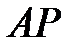 (или
(или 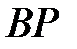 ), определяющее положение точки
), определяющее положение точки 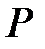 на прямой
на прямой 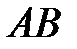 по формулам (с учетом знаков скоростей)
по формулам (с учетом знаков скоростей)


