Частные случаи движения точки

 

1. Равномерное движение ()

Касательное ускорение равно нулю .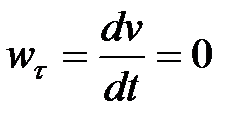

Напишем 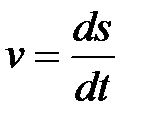, откуда . После интегрирования получим уравнение равномерного движения .

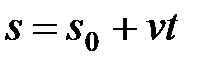Отсюда скорость 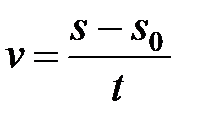, то есть является отношением пройденного пути во времени.

2. Прямолинейное движение ()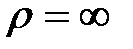

Нормальное ускорение равно нулю (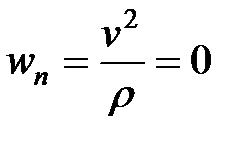), полное ускорение - касательному ().

При равномерном прямолинейном движении ускорение точки равно нулю ().

 

3. Равнопеременное движение ().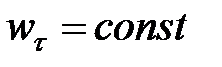

Алгебраическое значение скорости точки за равные промежутки времени изменяется на одну и ту же величину:

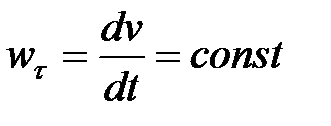, откуда .

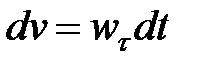После интегрирования имеем закон изменения скорости: .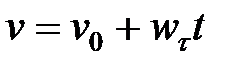

.

Интегрируя это выражение, получим уравнение равнопеременного движения .

При прямолинейном движении 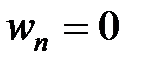, тогда 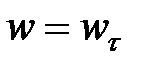, то есть полное ускорение равно касательному, индекс в таких случаях опускается.

 

 

Билет№12

Поступательное движение твердого тела

 

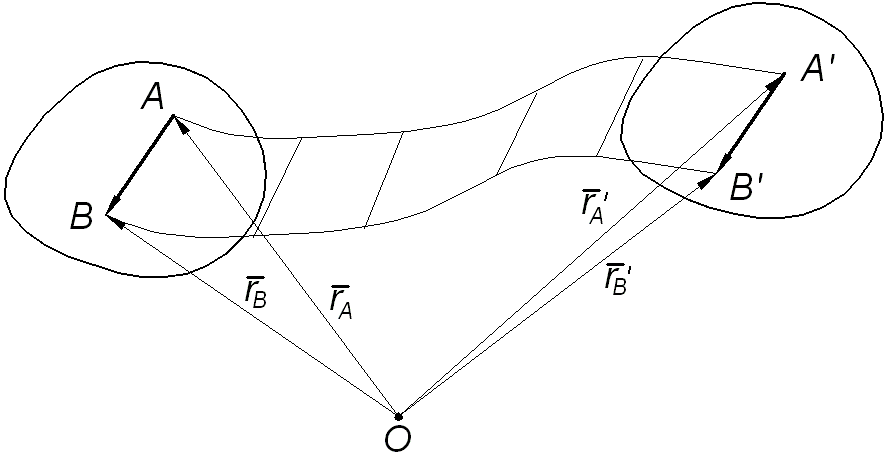
Движение тела, при котором всякая прямая, неподвижно связанная с ним, движется параллельно самой себе, называется поступательным. При этом траектории точек могут быть как прямыми, так и кривыми линиями.

Теорема. При поступательном движении тела все его точки движутся по одинаковым траекториям и имеют одинаковые скорости и ускорения.

Доказательство

В треугольнике (рис. 11.4)

(), (11.4)

.

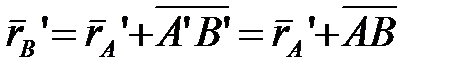Следовательно, траектория точки может быть получена смещением траектории точки в направлении постоянного вектора на расстояние , поэтому траектории точек и при наложении будут совпадать, то есть являются одинаковыми.

Дифференцированием выражения (11.4) по времени найдем соотношение между скоростями

Рис. 11.4

,

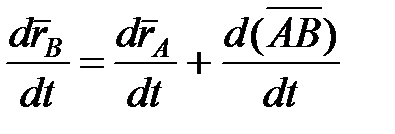где 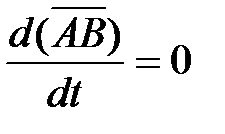, так как .

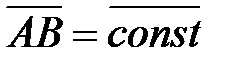Поскольку , , то скорости точек одинаковы: .

Далее, имеем , то есть , ускорения точек одинаковы.

Таким образом, поступательное движение твердого тела определено движением какой-либо одной точки. Скорости и ускорения точек тела называются скоростью и ускорением этого тела.

 

Билет№11

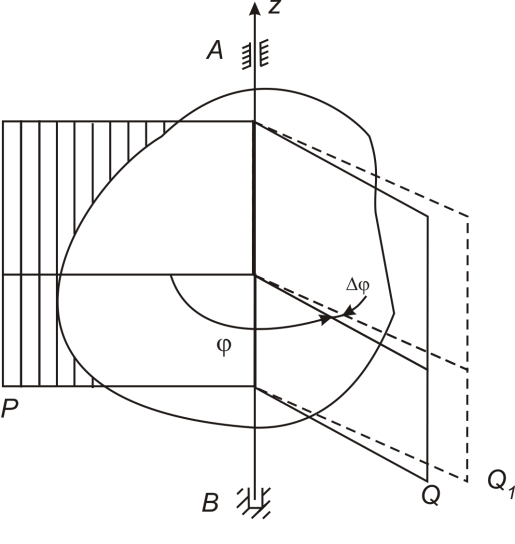Вращательным движением называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения. При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, описывая окружности с центрами на оси вращения.

Определим положение вращающегося тела следующим образом (рис. 12.1).

Задаемся направлением оси вращения . Через ось проведем две полуплоскости – неподвижную и подвижную , неизменно связанную с телом и вращающуюся с ним.

Рис. 12.1

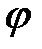Двугранный угол между этими полуплоскостями называется углом поворота тела.

Будем считать (положительным), если, глядя с конца оси , видим этот угол отложенным против хода часовой стрелки.

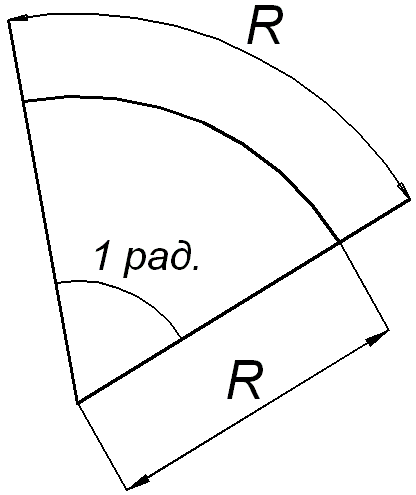Числовые значения угла в системе СИ измеряются в радианах. Радиан – центральный угол, соответствующий дуге окружности, длина которой равна радиусу (рис. 12.2): .

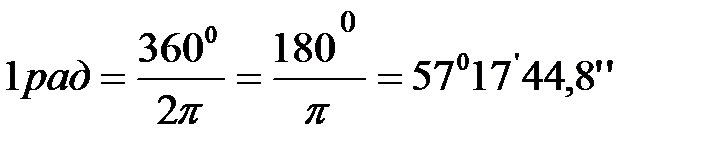Иногда угол поворота измеряется в оборотах 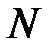, тогда в радианах он составляет .

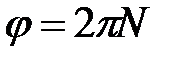Рис. 12.2

При вращении угол поворота изменяется со временем, следовательно, функционально зависит от времени:

.

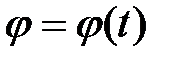Это выражение называется уравнением вращательного движения тела вокруг неподвижной оси, устанавливает зависимость между углом поворота тела и временем его движения.

Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростью тела .

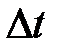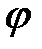Пусть за время подвижная полуплоскость повернулась на угол , а за время () - на угол .

Средней угловой скоростью за время называется отношение приращения угла 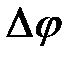ко времени :

.

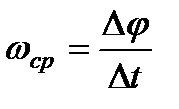Истинная угловая скорость в момент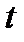

,

то есть равна первой производной угла поворота по времени.

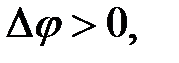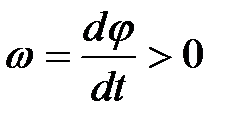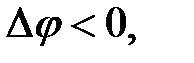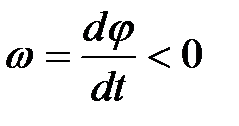Если то (угловая скорость положительна). Если то (угловая скорость отрицательна).

Размерность угловой скорости или .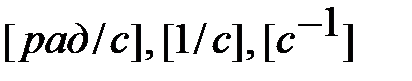

На практике нередко задается частость вращения , об/мин (число оборотов в минуту), тогда угловая скорость определяется соотношением , .

Величина 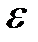, характеризующая быстроту изменения угловой скорости , называется угловым ускорением тела.

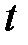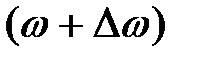Пусть в момент времени угловая скорость была , в момент () она составляла . Тогда среднее угловое ускорение за время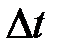

.

Истинное угловое ускорение в момент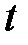

.

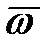
ω

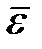
ε

Рис. 12.3

Угловое ускорение тела равно первой производной угловой скорости тела или второй производной угла поворота по времени.

Если угловая скорость и угловое ускорение имеют одинаковые знаки, то вращение ускоренное, а если разные, то замедленное.

Размерность углового ускорения

или .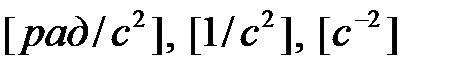

Вектор угловой скорости - вектор, равный по модулю 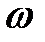и направленный вдоль оси вращения так, что, глядя с его конца, можно видеть вращение тела направленным противчасовой стрелки (рис. 12.3). Вектор углового ускорения определяется аналогично.

Траектории точек являются окружностями, лежащими в плоскостях, перпендикулярных к оси вращения, радиусы которых равны кратчайшим расстояниям от точек до оси вращения (рис. 12.4).

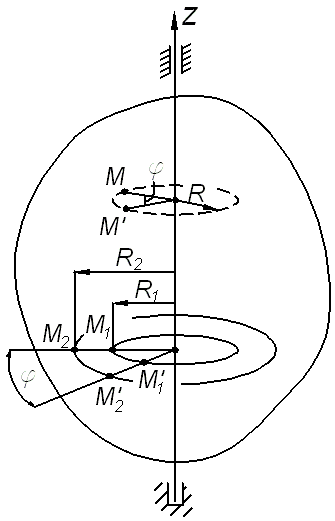
Рис. 12.4

φ

φ

Точки за одинаковые промежутки времени проходят расстояния, пропорциональные радиусам. Путь точки

.

Скорость точки (рис. 12.5)

 

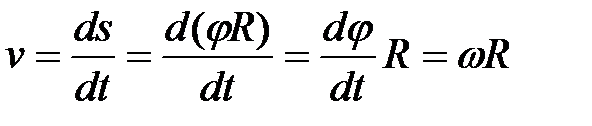, или .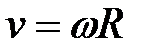

Рис. 12.4

Алгебраическое значение скорости точки равно произведению угловой скорости на расстояние от точки до оси вращения, направлена по касательной к траектории в сторону вращения тела.

О

R

ε

ω

Рис. 12.5

α

Касательное ускорение

, или ,

 

то есть равно произведению углового ускорения на расстояние от точки до оси вращения, направлено по касательной к траектории в сторону .

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: