 |
Нормальное (центростремительное) ускорение
|
|
|
|
, или 
,
то есть равно квадрату угловой скорости, умноженному на расстояние от точки до оси вращения, направлено к центру окружности, описанной точкой.
Модуль полного ускорения
, или 
.
Направление 
определяется углом 
: 
.
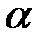Частные случаи вращательного движения
1. Равномерное вращение (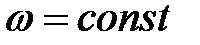
)
, откуда 
. После интегрирования получим уравнение равномерного вращения: 
.
Так как 
, то касательное ускорение равно нулю 
. Поэтому полное ускорение равно нормальному 
.
2. Равнопеременное вращение (
).
За равные промежутки времени угловая скорость изменяется на одну и ту же величину.
, откуда 
. После интегрирования находим закон изменения угловой скорости 
.
Определим закон вращения. 
.
После интегрирования получим уравнение равнопеременного вращения 
.
Отметим, что полученные уравнения аналогичны уравнениям, найденным ранее для движения точки.
|
| R |
|
|
|
| α |
| Рис. 12.6 |
|
|
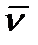
Векторные формулы для скоростей и ускорений
Легко убедиться, что вектор скорости любой точки равен векторному произведению: 
,
где 
- радиус-вектор точки с началом в любой точке, лежащей на оси вращения тела (рис. 12.6).
Это выражение называется векторной формулой Эйлера.
Направление скорости соответствует правилу определения направления векторного произведения.
Модуль скорости 
.
Справедливо также
Ускорение точки
Или 
.
Касательное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора углового ускорения на радиус-вектор этой точки относительно любой точки, лежащей на оси вращения
.
Нормальное (центростремительное) ускорение точки тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора угловой скорости на вращательную скорость этой точки
|
|
|
.
Билет№10
До сих пор речь шла о движении точки относительно неподвижной системы отсчета, за которую принята система, неподвижно связанная с Землей.
Движение точки по отношению к этой системе называется абсолютным.
Во многих задачах необходимо рассматривать движение точки как сложное (составное). В простейших случаях оно состоит из переносного и относительного движений.
Относительным движением называется движение точки по отношению к подвижной системе отсчета.
Переносным движением называется движение подвижной системы отсчета и всех связанных с ней точек относительно системы отсчета, принятой за неподвижную.
Удобно представить переносное движение точки, ее скорость и ускорение, если мысленно остановить относительное движение точки и определить ее скорость и ускорение относительно неподвижной системы отсчета как точки, неизменно связанной с подвижной системой отсчета.
Подобным образом можно, мысленно остановив переносное движение, представить относительное движение точки, ее скорость и ускорение по отношению к подвижной системе отсчета.
Условимся все характеристики обозначать индексами: 
- для абсолютного, 
- для переносного,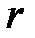 
- для относительного движений.
Абсолютной скоростью 
и абсолютным ускорением 
точки называются ее скорость и ускорение относительно системы отсчета, принятой за неподвижную.
Относительной скоростью 
и относительным ускорением 
точки называются скорость и ускорение точки по отношению к подвижной системе отсчета.
Переносной скоростью 
и переносным ускорением 
какой-либо точки 
называются абсолютная скорость и абсолютное ускорение той точки 
, неизменно связанной с подвижной системой отсчета, с которой совпадает в рассматриваемый момент данная точка М.
|
|
|
Теорема о сложении скоростей. Абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей:
| Рис. 13.1 |
|
.
Доказательство
Пусть точка 
движется относительно подвижной системы отсчета и вместе с ней движется относительно неподвижной системы отсчета (рис. 13.1).
Положение точки 
в подвижной системе отсчета 
характеризуется радиусом-вектором
, (13.1)
где 
- единичные векторы (орты) в подвижной системе отсчета.
Относительная скорость 
может быть получена дифференцированием радиуса-вектора 
по времени в предположении, что переносного движения нет, то есть орты 
являются постоянными векторами:
. (13.2)
Положение начала координат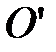 
определяется радиусом-вектором 
, а положение точки 
по отношению к неподвижной системе отсчета вектором 
.
Можно написать
. (13.3)
Вектор переносной скорости точки 
определяется дифференцированием вектора 
по времени в предположении, что относительного движения нет, то есть 
постоянные, а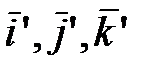 
изменяются:
. (13.4)
Абсолютную скорость точки 
находим дифференцированием выражения (13.3) по времени, считая все величины, входящие в него, переменными:
, (13.5)
откуда с учетом формул (13.2) и (13.4) следует
| Рис. 13.2 |
|
|
|
. (13.6)
Вектор абсолютной скорости определяется по правилу параллелограмма (рис. 13.2).
Билет№9 Начало в билете№10
Теорема Кориолиса о сложении ускорений. Абсолютное ускорение точки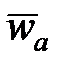 
при произвольном переносном движении равно геометрической сумме переносного 
, относительного 
и кориолисова (поворотного) 
ускорений:
. (13.7)
Доказательство
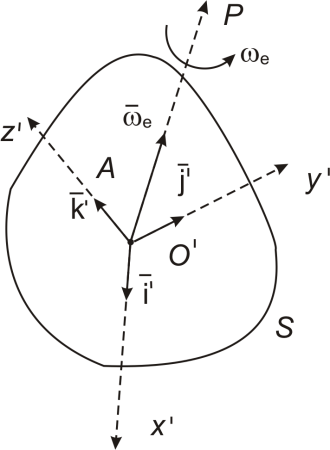
Пусть точка 
движется относительно подвижной системы отсчета 
, которая сама движется относительно неподвижной системы 
(рис. 13.3).
Произвольное движение твердого тела в общем случае можно представить как составное движение: переносное движение тела с какой-либо точкой 
(полюсом) и вращательного движения вокруг мгновенной оси 
, проходящей через выбранный полюс.
Обозначим угловую скорость вращения подвижной системы координат через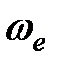 
и назовем ее переносной угловой скоростью.
| Рис. 13.3 |
при постоянных 
, находим переносное ускорение:|
|
|
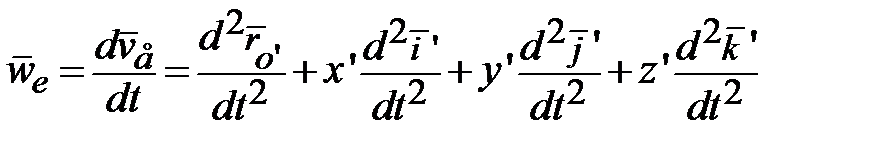. (13.8)
Дифференцируя выражение (13.2) по времени 
при постоянных 
, находим относительное ускорение:
. (13.9)
Дифференцируя выражение (13.5) по времени 
при всех переменных величинах, находим абсолютное ускорение:
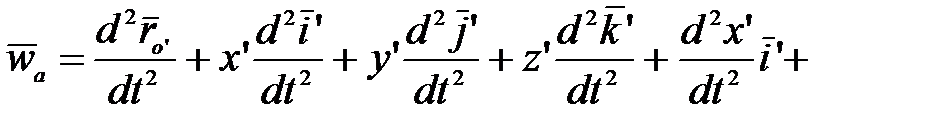
| Рис. 13.4 |
. (13.10)
Рассмотрим последний член выражения (13.10) (рис. 13.4).Заметим, что 
является радиусом-вектором точки 
относительно полюса 
, тогда скорость точки 
выражается производной по времени 
.
С другой стороны, 
.
Тогда 
. (13.11)
По аналогии имеем 
, 
.
Получены формулы Пуассона для дифференцирования единичного вектора.
Следовательно,
=
13.12)
Тогда на основании выражения (13.10) с учетом формул (13.8) и (13.9) имеем
, (13.13)
где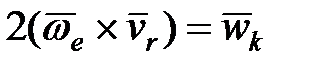 
- ускорение Кориолиса.
Следовательно, 
. (13.14)
Теорема доказана.
При поступательном переносном движении его угловая скорость равна нулю (
), поэтому отсутствует кориолисово ускорение (
). Следовательно,
, 13.15)
то есть при поступательном переносном движении абсолютное ускорение точки равно геометрической сумме векторов переносного и относительного ускорений.
Вектор кориолисова ускорения 
равен удвоенному векторному произведению угловой скорости переносного движения 
на относительную скорость точки 
:
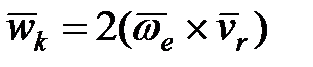. (13.16)
По модулю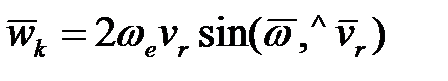 
, (13.17)
то есть модуль кориолисова ускорения 
равен удвоенному произведению модулей переносной угловой скорости 
и относительной скорости 
на синус угла между их векторами.
Кориолисово ускорение равно нулю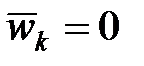 
в случаях, когдав рассматриваемый момент времени:
- переносная угловая скорость равна нулю (
),
- относительная скорость равна нулю (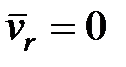
),
|
|
|
|
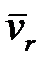
и 
параллельны (
|| 
), то есть 
.
Определение направления вектора 
1.
| Рис. 13.5 |
в данную точку, восстановить к плоскости векторов 
и 
перпендикуляр и направить вдоль него вектор 
так, чтобы с его конца можно было видеть кратчайшее совмещение первого вектора 
со вторым 
поворотом против хода часовой стрелки.
При < 
= 
.
2. Правило Н.Е. Жуковского (рис. 13.5). Для того чтобы определить направление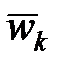 
, надо спроектировать вектор 
на плоскость, перпендикулярную к вектору 
и повернуть эту проекцию на угол 
в направлении переносной угловой скорости.
|
|
|
Билет№8
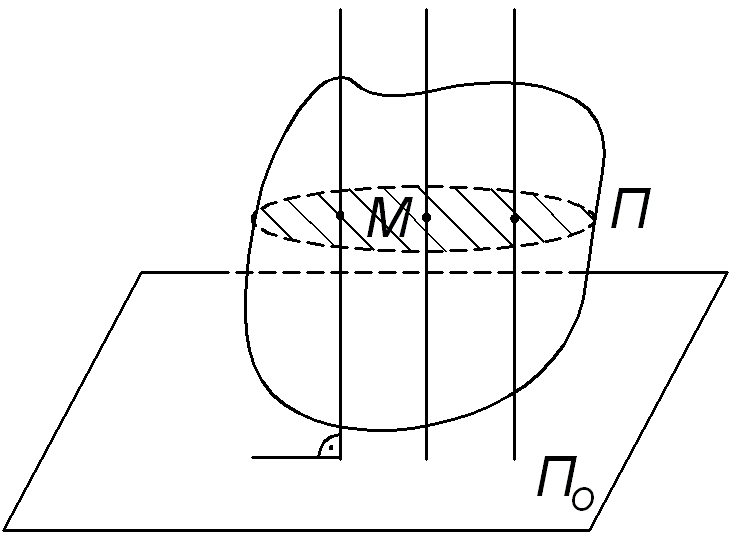Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется в одной и той же плоскости. Траектории точек являются плоскими линиями, плоскости которых параллельны между собой и параллельны одной неподвижной плоскости. Поэтому движение еще называется плоскопараллельным.
Это движение имеет большое значение в технике, так как звенья многих механизмов совершают плоское движение. Важно изучить способы задания плоского движения, определения скоростей и ускорений.
| Рис. 14.1 |
(рис. 14.1). Тогда прямая, перпендикулярная к этой плоскости и жестко скрепленная с движущимся телом, будет двигаться поступательно, то есть все ее точки движутся одинаково. Следовательно, для изучения движения этой прямой необходимо знать движение хотя бы одной ее точки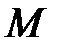 
. Рассуждая аналогично по отношению к другим прямым, перпендикулярным к плоскости 
, можно утверждать, что для изучения плоского движения тела достаточно изучить движение точек тела, лежащих в плоскости 
, параллельной заданной 
, которая образует плоскую фигуру.
Таким образом, для изучения плоского движения тела достаточно изучить движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости 
.
В общем случае за плоскую фигуру примем всю плоскость, жестко связанную с фигурой, и рассмотрим движение ее по отношению к другой, неподвижной, плоскости.
| Рис. 14.2 |
и направлением отрезка 
(рис. 14.2).
Произвольная точка 
, неразрывно связанная с движущейся фигурой и выбираемая для определения ее положения, называется полюсом.
Таким образом, зная координаты полюса 
и угол 
, можно определить движение тела. Их величины изменяются со временем и могут быть представлены функциями
.
Эти выражения являются уравнениями плоского движения твердого тела.
Зная их, можно определить уравнения движения любой точки тела:
,
,
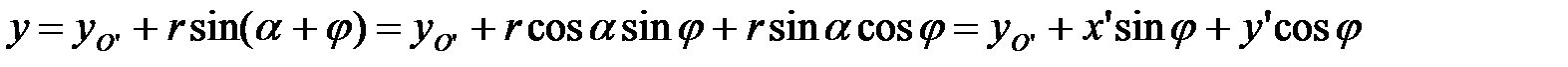или
,
,
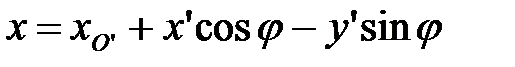что выражает собой уравнения движения произвольной точки 
плоской фигуры при движении в своей плоскости.
|
|
|
