 |
Как вынести множитель из-под корня?
|
|
|
|
Легко. Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:

Ничего сверхъестественного. Важно правильно выбрать множители. Здесь мы разложили 72 как 36·2. И всё получилось удачно. А могли разложить иначе: 72 = 6·12. И что!? Ни из 6, ни из 12 корень не извлекается... Что делать?!
Ничего страшного. Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:

Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:
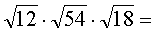
Перемножать всё - сумасшедшее число получится! И как потом из него корень извлекать?! Опять на множители раскладывать? Не, лишняя работа нам ни к чему. Сразу раскладываем на множители и собираем одинаковые по кучкам:

Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать. Главное - не ошибаться. Не человек для математики, а математика для человека!)
На этой оптимистической фразе завершим урок. Подведём итоги.
Обратите внимание. Всего одно свойство корней, одна небольшая формула умножения корней - и какие разнообразные возможности для практического применения!
Формула умножения корней позволяет:
-умножать корни,
-вносить число под корень,
-сравнивать корни,
-извлекать корни из больших чисел,
-выносить множитель из-под корня.
И все эти возможностивытекают из одной небольшого свойства корней. Мощное свойство, но... одно. Это - как табурет на одной ножке...) Сидеть можно, но с изрядными усилиями.
|
|
|
В нашем арсенале есть ещё два свойства корней. Одно - простое, второе - не очень. Но разобраться с ними можно и нужно. Оба этих свойства - в следующем уроке. Там же - примеры для тренировки. Там же описана одна тупая, но очень популярная ошибка в корнях, после которой люди бьют себя по голове и страшно ругаются...
Формулы корней. Свойства квадратных корней. Продолжение.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")
Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет деление корней.
Формула столь же проста, как и умножение. Вот она:

Напоминаю: здесь а - неотрицательное число (больше или равно нулю), b - положительное (больше нуля)! Иначе формула смысла не имеет... Об этих тонкостях мы ниже поговорим.
У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.
Как делить корни?
Элементарно. Вот вам примерчик:

В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:
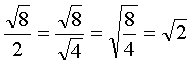
Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулу деления корней в дело употребить. Как видите, ничего здесь сложного нет.
Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:

Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!
|
|
|
В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:

Вот и все дела! От работы с дробью целиком, мы переходим к работе отдельно с числителем, отдельно со знаменателем. Что гораздо проще. А если дробь десятичная? Не вопрос! Если сразу корень не можете извлечь - переводите десятичную дробь в обыкновенную, и - вперёд! По формуле деления корней. Например:

Бывает ещё круче, когда корень из смешанного числа надо извлечь! Как поступаем? Правильно! Переводим смешанное число в неправильную дробь - и по знакомой формуле деления корней! К примеру, вот так:

Что, забыли, как переводить дроби? Срочно двигайте в тему "Дроби" и вспоминайте. А то ни дробь преобразовать, ни сократить её... И зачем вам тогда квадратные корни?
Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но... некомфортно.)
Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.
Можно ли корень возвести в квадрат? А почему нет? Умножить корень сам на себя - да все дела! И не только в квадрат можно. В любую степень. А извлечь корень из квадрата? Да тоже не проблема! Мы же умеем корень из произведения извлекать. Так что можно извлечь корень не только из квадрата, но и из любой степени.
Но именно эти действия вызывают массу проблем... С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.
|
|
|


