 |
Что такое квадратный корень?
|
|
|
|
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение - есть и вычитание. Есть умножение - есть и деление. Есть возведение в квадрат... Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:
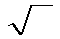
Сам значок называется красивым словом " радикал ".
Как извлечь корень? Это лучше рассмотреть на примерах.
Как извлечь (или посчитать - это всё едино) корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да конечно же 2! Значит:
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
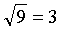
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
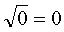
Уловили, что такое квадратный корень? Тогда считаем примеры:
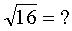
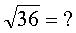
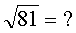
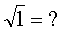
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но... Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек... Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень...
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах...
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию - возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться...
|
|
|
В этом и есть сложность извлечения корней. Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком - да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс - подбор ответа - сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 - вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да...
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый - выучить таблицу квадратов. Это здорово поможет решать примеры. Второй - решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно...
Итак, что такое квадратный корень, КАК извлекать корни - думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
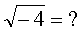
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 22 даёт +4. (-2)2 даёт опять +4! Вот-вот... Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт - сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
|
|
|
Выражение, в котором под знаком квадратного корня стоит отрицательное число - не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных - можно. Например, вполне можно вычислить
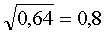
или
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить... Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
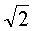
или
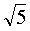
и т.д...
Ничего страшного. Всё то же самое. Корень квадратный из двух - это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное... Вот оно:
Что интересно, эта дробь не кончается никогда... Такие числа называются иррациональными. В квадратных корнях это - самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
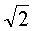
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
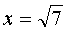
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
, 
, ......
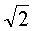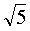и так далее, скрываются просто числа! Неровные, лохматые, иррациональные, но числа!
Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например
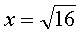
никто не оценит... Надо корень посчитать и написать
х = 4.
А вот
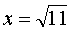
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
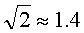
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Идём дальше.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах... Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два - слышу недовольные ответы...
Верно. Два. Но ведь и минус два даст в квадрате 4... А между тем, ответ
|
|
|
правильный, а ответ
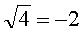
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2)2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит... Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: арифметический квадратный корень из числа а - это неотрицательное число, квадрат которого равен а. Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни - арифметические. Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше - не возиться с отрицательными результатами... Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
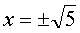
Такой ответ (совершенно правильный, кстати) - это просто сокращённая запись двух ответов:
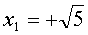
и
Стоп-стоп! Чуть выше я написал, что квадратный корень - число всегда неотрицательное! А здесь один из ответов - отрицательный! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням... Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
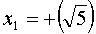
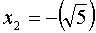
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня. Теперь наглядно видно, что сам корень (в скобках) - число всё равно неотрицательное! А знаки - это результат решения уравнения. Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
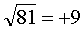
Потому, что это - арифметический квадратный корень.
Но если вы решаете какое-нибудь квадратное уравнение, типа:
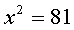
то всегда получается два ответа (с плюсом и минусом):
|
|
|
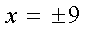
Потому, что это - решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор... извините, камни!)
Всё это - в следующих уроках.
|
|
|
