 |
Связь между тригонометрическими функциями одного угла.
|
|
|
|
Да, конечно. Синус, косинус, тангенс и котангенс одного и того же угла связаны между собой. Всякая связь между выражениями задаётся в математике формулами. В тригонометрии формул - колоссальное количество. Но здесь мы рассмотрим самые основные. Эти формулы так и называются: основные тригонометрические тождества. Вот они:



Эти формулы надо знать железно. Без них вообще в тригонометрии делать нечего. Из этих основных тождеств вытекают ещё три вспомогательных тождества:

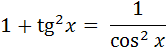

В каких заданиях и как используются основные тригонометрические тождества? Самое популярное задание - найти какую-нибудь функцию угла, если дана другая. В ЕГЭ такое задание из года в год присутствует.) Например:
Найти значение sinx, если х - острый угол, а cosx=0,8.
Задачка почти элементарная. Ищем формулу, где имеются синус и косинус. Вот она эта формула:
sin2x + cos2x = 1
Подставляем сюда известную величину, а именно, 0,8 вместо косинуса:
sin2x + 0,82 = 1
Ну и считаем, как обычно:
sin2x + 0,64 = 1
sin2x = 1 - 0,64
sin2x = 0,36
Вот, практически и всё. Мы вычислили квадрат синуса, осталось извлечь квадратный корень и ответ готов! Корень из 0,36 будет 0,6.
sinx = 0,6
Задачка почти элементарная. Но словечко "почти" здесь не зря стоит... Дело в том, что ответ sinx= - 0,6 тоже подходит... (-0,6)2 тоже 0,36 будет.
Два разных ответа получаются. А нужен один. Второй - неправильный. Как быть!? Да как обычно.) Внимательно прочитать задание. Там зачем-то написано:... если х - острый угол... А в заданиях каждое слово смысл имеет, да... Эта фраза - и есть дополнительная информация к решению.
Острый угол - это угол меньше 90°. А у таких углов все тригонометрические функции - и синус, и косинус, и тангенс с котангенсом - положительные. Т.е. отрицательный ответ мы здесь просто отбрасываем. Имеем право.
|
|
|
Собственно, восьмиклассникам такие тонкости не нужны. Они работают только с прямоугольными треугольниками, где углы могут быть только острые. И не знают, счастливые, что бывают и отрицательные углы, и углы в 1000°... И у всех этих кошмарных углов есть свои тригонометрические функции и с плюсом, и с минусом...
А вот старшеклассникам без учёта знака - никак. Многие знания умножают печали, да...) И для правильного решения в задании обязательно присутствует дополнительная информация (если она необходима). Например, она может быть дана такой записью:

Или как-нибудь иначе. В примерах ниже увидите.) Для решения таких примеров нужно знать, в какую четверть попадает заданный угол х и какой знак имеет нужная тригонометрическая функция в этой четверти.
Эти азы тригонометрии рассмотрены в уроках что такое тригонометрический круг, отсчёт углов на этом круге, радианная мера угла. Иногда требуется знать и таблицу синусов косинусов тангенсов и котангенсов.
Итак, отметим самое главное:
Практические советы:
1. Запомните определения синуса, косинуса, тангенса и котангенса. Очень пригодится.
2. Чётко усваиваем: синус, косинус, тангенс и котангенс накрепко связаны с углами. Знаем одно - значит, знаем и другое.
3. Чётко усваиваем: синус, косинус, тангенс и котангенс одного угла связаны между собой основными тригонометрическими тождествами. Знаем одну функцию - значит, можем (при наличии необходимой дополнительной информации) вычислить все остальные.
А теперь порешаем, как водится. Сначала задания в объёме 8-го класса. Но и старшеклассникам тоже можно...)
1. Вычислить значение tgА, если ctgА = 0,4.
2. β - угол в прямоугольном треугольнике. Найти значение tgβ, если sinβ = 12/13.
3. Найти значение выражения:
6sin25° - 3 + 6cos25°
4. Найти значение выражения:
(1-cosx)(1+cosx), если sinх = 0,3
5. Определить синус острого угла х, если tgх = 4/3.
|
|
|
Ответы (через точку с запятой, в беспорядке):
0,09; 3; 0,8; 2,4; 2,5
Получилось? Отлично! Восьмиклассники могут уже пройти за своими пятёрками.)
Это были задачки типа ЕГЭ, но в урезанном варианте. ЕГЭ - лайт). А сейчас почти такие же задания, но в полноценном егэшном виде. Для обременённых знаниями старшеклассников.)
6. Найти значение tgβ, если sinβ = 12/13, а

7. Определить sinх, если tgх = 4/3, а х принадлежит интервалу (- 540°; - 450°).
8. Найти значение выражения sinβ·cosβ, если ctgβ = 1.
Ответы (в беспорядке):
-0,8; 0,5; -2,4.
Здесь в задаче 6 угол задан как-то не очень однозначно... А в задаче 8 и вовсе не задан! Это специально). Дополнительная информация не только из задания берётся, но и из головы.) Зато уж если решили - одно верное задание "В" гарантировано!
В этом уроке дано очень ограниченное понятие тригонометрических функций. В пределах 8-го класса. А у старших остаются вопросы...
Например, если угол х (смотрите вторую картинку на этой странице) - сделать тупым!? Треугольник-то вообще развалится! И как быть? Ни катета не будет, ни гипотенузы... Пропал синус...
Если бы древние люди не нашли выход из этого положения, не было бы у нас сейчас ни мобильников, ни TV, ни электричества. Да-да! Теоретическая основа всех этих вещей без тригонометрических функций - ноль без палочки. Но древние люди не подвели. Как они выкрутились - в следующем уроке.
|
|
|


