 |
Когерентными являются волны одной природы, с одинаковыми частотами и неизменной во времени разностью начальных фаз, распространяющиеся вдоль одной прямой, и поляризованные в одной плоскости.
|
|
|
|
Волновая оптика
Развитие взглядов на природу света
В 1621 году голландский физик Виллеборд Снеллиус (1580 – 1626) работая в Лейденском университете, установил закон преломления света. Математическую запись в виде 
(для каждой пары сред) дал французский философ, физик и математик Рене Декарт (1596 – 1650). Он же пытался объяснить этот закон с позиций корпускулярной природы света (корпускула – частица).
Исаак Ньютон (1643 – 1727) также придерживался корпускулярной природы света. Но уже во времена Ньютона возникла и развивалась волновая теория света. Теория Гука-Гюйгенса. Роберт Гук (1635 – 1703) английский физик. Христиан Гюйгенс (1629 – 1695) голландский физик, механик, математик. Из волновой природы света родился принцип Ферма – лучи света распространяются так, чтобы пройти путь за кратчайшее время. Пьер Ферма (1601 – 1665) французский математик и физик. В 1801 году английский физик Томас Юнг (1788 – 1827) установил принцип интерференции, высказал идею поперечности световых волн и, что световые и тепловые лучи отличаются только длиной волны.
В 1818 году французский физик Огюстен Жан Френель (1788 -1827), кстати, по образованию инженер по ремонту и строительству дорог, открыл поляризацию света. За объяснение дифракции света получил премию Парижской академии наук.
В 1846 году английский физик Майкл Фарадей (1791 – 1867) открыл явление вращения плоскости поляризации света магнитным полем. Т.е. установил связь оптических и магнитных (электрических) явлений.
В 1865 году английский физик Джеймс Кларк Максвелл (1831 – 1879) доказал электромагнитную природу света.
Но начался двадцатый век, и все споры начались сначала. В 1905 году немецкий физик Альберт Эйншейн (1879 – 1955) объяснил фотоэффект с позиций корпускулярной природы света. В 1922 году американский физик Артур Комптон (1892 – 1962) окончательно доказал, электромагнитные волны рентгеновского (коротковолнового) излучения одновременно являются и корпускулами (фотоны) и волнами.
|
|
|
Итак, свет имеет двойственную природу. Это называется корпускулярно-волновой дуализм.
В этом семестре мы будем рассматривать только волновые свойства света.
Рассмотрим вначале оптические диапазоны длин волн.
Оптический диапазон длин волн обычно подразделяют на:
- ультрафиолетовое излучение - 
=0,01 
0,40 мкм;
- видимое излучение (свет) - =0,40 0,76 мкм;
- инфракрасное излучение - =0,76 мкм несколько мкм;
Длины волн указаны для вакуума.
В электромагнитной волне колеблются векторы 
и 
. Из опытов известно, что многие действия света вызываются колебаниями электрического вектора. Поэтому в дальнейшем мы будем говорить о световом векторе, подразумевая под ним вектор напряженности электрического поля. Соответственно, уравнение световой волны будет выглядеть так:
,
– модуль амплитуды светового вектора;
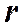– расстояние, отсчитываемое вдоль направления распространения световой волны.
Для плоской волны, распространяющейся в не поглощающей среде, 
, для сферической волны убывает как 
.
Интерференция света
Допустим, что в некоторой области перекрываются две волны. В области перекрытия наблюдается сложение (суперпозиция) волн и после выхода из этой области каждая волна распространяется так, как если бы никакого перекрытия не было. В каждой точке области перекрытия происходит сложение колебаний, создаваемых проходящими волнами. Результаты таких сложений определяются тем, являются перекрывшиеся волны когерентными или нет.
Когерентными являются волны одной природы, с одинаковыми частотами и неизменной во времени разностью начальных фаз, распространяющиеся вдоль одной прямой, и поляризованные в одной плоскости.
|
|
|
Сложение когерентных волн называется интерференцией. При интерференции в каждой точке области перекрытия волн устанавливается гармонический колебательный процесс с постоянной амплитудой, различной в разных точках. При перекрытии некогерентных волн возникают негармонические колебательные процессы с нерегулярно изменяющимися амплитудами. Вся область перекрытия в этом случае воспринимается равномерно освещенной.
Реальные источники световых волн обеспечить когерентное излучение не могут. Однако, используя специальные приемы, когерентные волны можно получить и от обычных источников. Для этого волну, излучаемую одним источником света, разделяют каким – либо способом на две части, а затем их накладывают друг на друга.
Рассмотрим интерференцию волн от двух точечных когерентных источников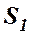 
и 
. Рассмотрение ведём для вакуума. Допустим, что точка наблюдения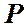 
удалена от этих источников на расстояния 
и 
, значительно превышающие расстояние 
между источниками: 
, 
. В таких условиях направления колебаний, создаваемых волнами в точке 
, практически совпадают и сложение колебаний можно проводить в скалярной форме. Уравнения этих колебаний имеют вид:
Если сопоставить эти уравнения с уравнениями гармонических колебаний, то видно, что произведения 
и 
исполняют роль начальных фаз:
,
При сложении двух одинаково направленных гармонических колебаний с равными частотами возникает гармоническое колебание, описываемое уравнением:
,
где 
- начальная фаза результирующего колебания,
;
- амплитуда результирующего колебания,
Записав разность фаз через произведения и 
, получим:
.
Отсюда следует, что амплитуда результирующего колебания зависит от расположения точки наблюдения относительно источников. В полученном выражении 
– геометрическая разность хода волн. Рассмотрим два предельных случая:
1. Пусть выполняется следующее условие:
,
где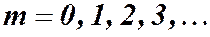 
. Из выражения для амплитуды при этом следует: 
, т.е. амплитуда результирующего колебания равна сумме амплитуд колебаний, созданных интерферирующими волнами. Такие точки называются максимумами интерференции. Условие максимумов:
|
|
|
Таким образом, максимумы интерференции наблюдаются в точках, для которых разность хода волн от источников равна четному числу полуволн. При такой разности хода волны имеют одинаковые фазы, что и приводит к сложению их амплитуд.
2. Пусть теперь выполняется такое условие:
,
где 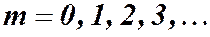Из выражения для амплитуды при этом следует: 
. Если 
, то 
, результирующее колебание отсутствует. Такие точки называются минимумами интерференции. Условие минимумов:
Таким образом, минимумы интерференции наблюдаются в точках, для которых разность хода волн от источников равна нечетному числу полуволн. При такой разности хода волны имеют противоположные фазы, и поэтому частично или полностью гасят друг друга.
Если световые волны распространяются не в вакууме, а в среде, то необходимо учесть показатель преломления среды.
Тогда получаем 
Т.е. в выражениях вместо l0 необходимо записать l.
Вспомним, что интенсивность волны пропорциональна квадрату амплитуды:
.
Поэтому для волн, приходящих в точку наблюдения, имеем: 
, 
. Суммарная интенсивность этих волн 
.
В случае некогерентных волн разность фаз Dj непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее значение ácosDjñ = 0 (он изменяется от – 1 до + 1). Поэтому получаем.
Отсюда можно записать выражение для интенсивности при сложении некогерентных волн.
Т.е. интенсивность света, наблюдаемая при сложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности.
В случае когерентных волн ácosDjñ = const (для каждой точки пространства) так, что для интенсивностей запишем.
Отсюда следует, что 
, т.е. интенсивность в областях максимумов больше суммы интенсивностей приходящих в эти области волн. Соответственно, легко придти к выводу о том, что интенсивность в областях минимумов меньше суммы интенсивностей приходящих в эти области волн. Т.о. при наложении когерентных волн будет происходить перераспределение светового потока в пространстве, в результате в одних местах будет максимум, а в других – минимум интенсивности. Это явление и называется интерференцией волн.
|
|
|
Эти результаты не противоречат закону сохранения энергии, поскольку при интерференции в зоне перекрытия волн происходит пространственное перераспределение энергии. Часть энергии из области минимумов энергии перемещается в области максимумов.
Особенно отчётливо интерференция проявляется, когда I1 = I2. Тогда в максимуме будет I = 4×I1, а в минимуме I = 0.
Картина интерференции приведена на рисунке. В точке наблюдения , в зависимости от разности хода волн образуется минимум либо максимум интенсивности волны.
|
|
|
