 |
Интерференция от пластинки переменной толщины
|
|
|
|
Пусть пластинка имеет форму клина с малым углом 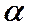 при вершине
при вершине  . Пусть на нее падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2. Отразившиеся от разных поверхностей пластинки лучи теперь не будут параллельными. Из всех лучей, на которые разделился падающий луч 1, рассмотрим только лучи
. Пусть на нее падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2. Отразившиеся от разных поверхностей пластинки лучи теперь не будут параллельными. Из всех лучей, на которые разделился падающий луч 1, рассмотрим только лучи 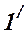 и
и  , отразившиеся от верхней и нижней поверхностей клина. Эти лучи когерентны, пересекутся в точке
, отразившиеся от верхней и нижней поверхностей клина. Эти лучи когерентны, пересекутся в точке 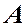 и соберутся линзой на экране в точке
и соберутся линзой на экране в точке 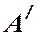 , которая является изображением точки
, которая является изображением точки 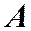 . Если источник света расположен далеко от клина и угол
. Если источник света расположен далеко от клина и угол 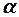 очень мал, то оптическая разность хода между интерферирующими лучами
очень мал, то оптическая разность хода между интерферирующими лучами  и
и 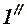 может быть с достаточной степенью точности вычислена по формуле для плоскопараллельной пластинки:
может быть с достаточной степенью точности вычислена по формуле для плоскопараллельной пластинки:
 |
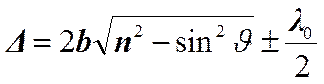 .
.
В этой формуле в качестве параметра 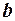 берется толщина клина в месте падения на него луча 1. Лучи
берется толщина клина в месте падения на него луча 1. Лучи 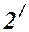 и
и 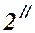 , образовавшиеся за счет деления луча 2, падающего в другую точку клина, собираются линзой в точке
, образовавшиеся за счет деления луча 2, падающего в другую точку клина, собираются линзой в точке 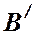 . Оптическая разность хода лучей в этой точке определяется толщиной клина
. Оптическая разность хода лучей в этой точке определяется толщиной клина  . Таким образом, на экране возникнет система интерференционных полос за счет отражения от мест пластинки, имеющих одинаковую толщину. Это полосы равной толщины. Полосы равной толщины локализованы вблизи поверхности клина.
. Таким образом, на экране возникнет система интерференционных полос за счет отражения от мест пластинки, имеющих одинаковую толщину. Это полосы равной толщины. Полосы равной толщины локализованы вблизи поверхности клина.
Интерференционная картина, образующаяся при отражении от клина, получается пространственно локализованной. При изменении положения экрана условия наблюдения интерференции могут ухудшаться. Всегда хуже наблюдается картина у основания клина, а лучше – у его вершины. С линзой интерференционная картина наблюдается лучше. Но в качестве линзы может "сработать" хрусталик глаза. Поэтому мы и наблюдаем радужные картинки у мыльных пузырей, от разлитого на поверхности воды бензина, цвета побежалости (окисные плёнки) на поверхности металлов.
|
|
|
Итак: полосы равного наклона получаются при освещении плоскопараллельной пластинки постоянной толщины (b = const) рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина, b ¹ const) параллельным пучком света.
Кольца Ньютона
 Кольца Ньютона являются классическим примером полос равной толщины. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки играет воздушный зазор между пластиной и линзой. При нормальном падении света в отраженном свете наблюдаются концентрические окружности с центром в точке соприкосновения линзы с пластинкой. При наклонном падении света интерференционная картина принимает вид эллипса.
Кольца Ньютона являются классическим примером полос равной толщины. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки играет воздушный зазор между пластиной и линзой. При нормальном падении света в отраженном свете наблюдаются концентрические окружности с центром в точке соприкосновения линзы с пластинкой. При наклонном падении света интерференционная картина принимает вид эллипса.
Рассмотрим отражённый свет.
Найдем радиусы темных колец (минимумов) 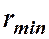 . Запишем условие образования минимумов.
. Запишем условие образования минимумов.
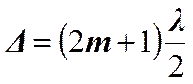
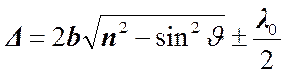 .
.
При нормальном падении света угол 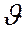 равен нулю,
равен нулю, 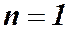 (воздушный зазор). Тогда
(воздушный зазор). Тогда  (полуволна "теряется" при отражении от пластинки) и условие минимумов запишется в виде:
(полуволна "теряется" при отражении от пластинки) и условие минимумов запишется в виде:
 . Отсюда
. Отсюда 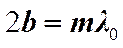 .
.
Из теоремы Пифагора следует:  . Поскольку
. Поскольку 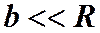 , пренебрежем
, пренебрежем 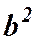 . Получим
. Получим  . Подставим это выражение в условие для минимумов
. Подставим это выражение в условие для минимумов 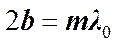 :
:
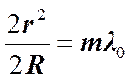 или
или 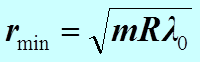 , где
, где 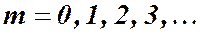
Получили выражение для радиуса 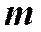 - го темного кольца.
- го темного кольца.
Найдем радиусы светлых колец (максимумов) 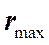 . Запишем условие образования максимумов.
. Запишем условие образования максимумов.
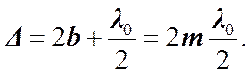 Отсюда.
Отсюда.
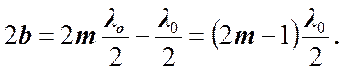 Подставим выражение для b и получим.
Подставим выражение для b и получим.
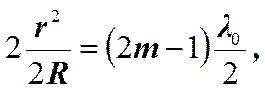
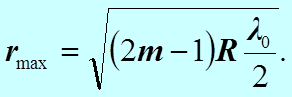
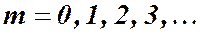
Получили выражение для радиуса 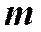 - го светлого кольца в отражённом свете.
- го светлого кольца в отражённом свете.
Рассмотрим случай, когда m = 0.
 Это физически бессмысленно. Следовательно, в центре будет наблюдаться темное пятно, минимум.
Это физически бессмысленно. Следовательно, в центре будет наблюдаться темное пятно, минимум.
Кольца Ньютона можно наблюдать и в проходящем свете. В этом случае луч света дважды изменил фазу на p, и поэтому условия максимума и минимума меняются местами.
|
|
|
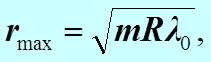
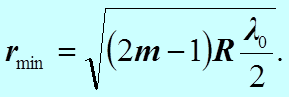
Если между плоскопараллельной пластинкой и линзой находится не воздух, а какая-то среда с показателем преломления n ¹ 1, то в приведённых выше формулах для радиусов колец Ньютона, необходимо заменить длину волны в вакууме l0 на длину волны в данной среде.
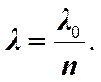
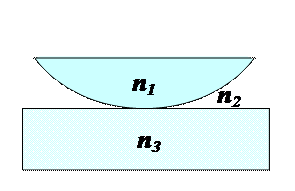 В центре в отражённом свете наблюдается темное пятно, а в проходящем – светлое пятно.
В центре в отражённом свете наблюдается темное пятно, а в проходящем – светлое пятно.
Можно и в отражённом свете получить в центре светлое пятно, если пространство между линзой и плоскопараллельной пластинкой заполнено веществом, удовлетворяющее условию: n3 > n2 > n1.
|
|
|


