 |
Интерференция при отражении от тонких пластинок
|
|
|
|
При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые могут интерферировать. На пластинке происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения.
Пусть на прозрачную плоскопараллельную пластинку под углом 
(тета) относительно нормали к пластинке падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отражает вверх два параллельных пучка света, один из которых образовался за счет отражения от верхней поверхности пластинки, другой – от нижней поверхности. Кроме этих двух пучков пластинка отбросит вверх и другие пучки, которые возникают в результате трех, пятикратного и т.д. отражения от поверхностей пластинки. Однако эти пучки имеют малую интенсивность, в связи, с чем их вклад в интерференционную картину невелик.
Амплитуды двух рассматриваемых пучков света (волн) мало отличаются друг от друга, что важно для получения контрастной картины интерференции. Определим оптическую разность хода 
отраженных волн 1 и 2.
– показатель преломления среды.
Избавимся от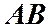 
, 
и 
. Из геометрических соображений можно записать: 
; 
, 
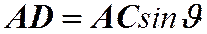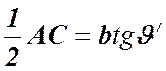, следовательно, 
, тогда 
. В этих выражениях 
– толщина пластинки. В итоге получим:
.
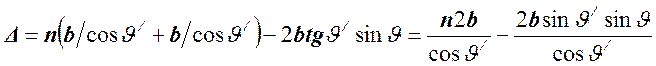Из закона преломления следует, что 
. Подставив это соотношение в предыдущую формулу, получим
В полученном выражении необходимо учесть, что при отражении волны от оптически более плотной среды (в рассматриваемом случае от верхней поверхности пластинки) ее фаза изменяется скачком на величину 
. Этот вопрос мы рассматривали в разделе волны. Возникающую дополнительную разность фаз можно учесть, добавив к 
или вычтя из нее половину длины волны в вакууме. В результате получим:
|
|
|
.
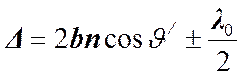Избавимся от угла 
: 
, следовательно,
.
Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется полученной формулой. Теперь важно определить условия, при которых волны окажутся когерентными и смогут интерферировать. Волны смогут интерферировать, если наблюдается временная и пространственная когерентность.
а) Условие временной когерентности.
Для обеспечения временной когерентности разность хода 
не должна превышать длину когерентности 
. Запишем это условие:
.
Это означает, что для толщины пластинки должно выполняться условие:
.
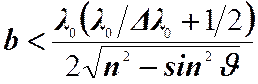Упростим выражение. Пренебрежем 
по сравнению с 
. Учтем также, что 
имеет величину порядка единицы. Тогда условие временной когерентности можно записать в следующем виде.
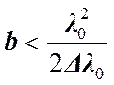, или 
– удвоенная толщина пластинки должна быть меньше длины когерентности. Пусть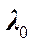 
=0,5мкм, 
=0,02мкм. Предельное значение толщины пластинки при этом около 0,06 мм.
б) Условие пространственной когерентности.
Вспомним, что пространственная когерентность световой волны характеризуется параметром, который называется шириной когерентности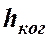 
. Это величина, пропорциональная отношению длины волны 
к угловому размеру 
источника светового излучения: 
. Отраженные от верхней и нижней поверхностей пластинки лучи будут интерферировать в том случае, если расстояние 
между лучами не превышает половины ширины когерентности: 
. Запишем условие пространственной когерентности без вывода.
Выполнение этого условия будет зависеть от угла падения лучей 
. Чем меньше угол падения, тем меньше 
и менее существенным становится для получения интерференционной картины параметр 
источника светового излучения.
|
|
|
Таким образом, волны будут интерферировать, если выполняются записанные условия временной и пространственной когерентности. Интерференционная картина будет наблюдаться в виде системы полос, причем при 
будут наблюдаться максимумы, а при 
– минимумы. Подставив в эти условия выражение для 
, получим для максимумов в отражённом свете.
,
и для минимумов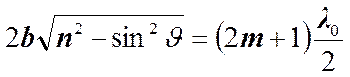 
.
Интерференционную картину при отражении световых лучей от тонких пленок обычно наблюдают с помощью линзы, в фокальной плоскости которой располагается экран. Линза не изменяет оптической разности хода между лучами и, следовательно, не изменяет разности фаз, но собирает в одну точку лучи падающие под одним углом на пластинку. На экране наблюдается система чередующихся светлых и темных круговых полос. Каждая полоса будет образована лучами, падающими на пластинку под одинаковым углом 
. В связи с этим интерференционные полосы называются полосами равного наклона. Локализованы полосы равного наклона в бесконечности.
Если использовать параллельный пучок света (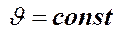
), то разность хода лучей D для всех лучей будет одинаковой и чередующиеся темные и светлые полосы не будут наблюдаться. Будет одинаково освещённый экран, соответствующий максимуму или минимуму (или промежуточному значению) интерференции.
Все рассуждения были проведены нами для отраженного света. Интерференцию можно наблюдать и в проходящем свете. Особенность – в проходящем свете потери полуволны не наблюдается, оптическая разность хода волн для проходящего и отраженного света отличается на 
. В связи с этим, например, максимуму интерференции в отраженном свете соответствует минимум в проходящем свете.
Максимум.
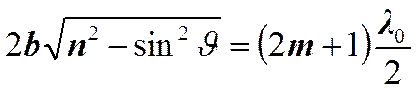
Минимум.
|
|
|
