 |
Ширина полос интерференции
|
|
|
|
 Введем еще два параметра интерференционной картины. Ширина интерференционной полосы
Введем еще два параметра интерференционной картины. Ширина интерференционной полосы  – это расстояние между двумя соседними минимумами, а расстояние между двумя интерференционными полосами – это расстояние между двумя соседними максимумами интенсивности. Ясно, что эти оба параметра имеют одинаковое значение. Из геометрических соображений получим это.
– это расстояние между двумя соседними минимумами, а расстояние между двумя интерференционными полосами – это расстояние между двумя соседними максимумами интенсивности. Ясно, что эти оба параметра имеют одинаковое значение. Из геометрических соображений получим это.
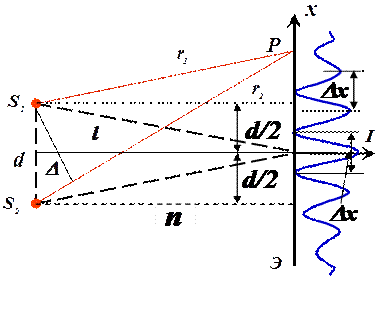
Рассмотрим две световые волны, исходящие из точечных источников S1 и S2. n – показатель преломления среды. Экран параллелен прямой соединяющей источники. Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование мест с максимумом и минимумом интенсивности света. Вычислим ширину полос интерференции Dx (тёмных и светлых полос). Положение точки на экране будет характеризоваться точкой x, отстоящей от центрального максимума (расположен на перпендикуляре, опущенном из середины расстояния между источниками). Установим, что источники колеблются в одинаковой фазе.
Из рисунка видно.
|
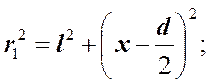
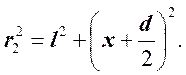




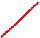



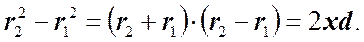 (2)
(2)
Т.к. d << l и x << l, то можно считать.
 (3)
(3)
Тогда из (2) и (3) получаем.

 – это геометрическая разность хода. (5)
– это геометрическая разность хода. (5)
Умножим левую и правую части (5) на показатель преломления среды n.
 – это оптическая разность хода.
– это оптическая разность хода.
 (6)
(6)
Подставим это значение в условие максимума интенсивности.
 Для среды.
Для среды.  (7)
(7)
m = 0, 1, 2 … 
Для условия минимума имеем.
 Получим.
Получим.  (8)
(8)
Из формул (7) и (8) видно, что расстояние между полосами и ширина полосы имеют одинаковое значение, равное:
 , где
, где  – расстояние от источников до экрана.
– расстояние от источников до экрана.
Из перечисленных формул видно, что при d» l, Dx» l, т.е. ширина полосы была бы сравнима с длиной волны, т.е. Dx < 1 мкм. Ничего нельзя было бы увидеть. Поэтому необходимо выполнение условия d << l.
|
|
|
Из приведённых формул видно, что ширина интерференционной полосы и расстояние между полосами зависит от длины волны l. Только в центре интерференционной картины при x = 0 совпадают максимумы всех длин волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга всё больше и больше. Это приводит к тому, что при наблюдении в белом свете, происходит размытие интерференционных полос. Интерференционная картина будет окрашенной, но не чёткой, смазанной.
Измерив Dx, зная l и d можно вычислить длину волны света l. Именно так впервые вычислили длины волн разных цветов.
Когерентность
Необходимым условием интерференции волн является их когерентность. Условию когерентности удовлетворяют монохроматические волны. Однако монохроматическая волна, описываемая выражением 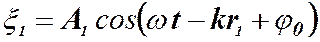
представляет собой абстракцию. Следовательно, рассмотренный нами процесс интерференции является идеализированным. Волны, излучаемые любыми независимыми источниками света, не могут быть монохроматическими и когерентными. Причина немонохроматичности, следовательно, некогерентности световых волн лежит в самой природе происхождения этих волн. Излучение светящегося тела слагается из волн, испускаемых атомами. Излучение каждого атома длится очень короткое время (порядка 10-8 с). За это время возбужденный атом переходит в нормальное состояние и перестает излучать. Возбудившись вновь, атом начинает испускать световые волны уже с новой начальной фазой. Разность фаз между излучением двух независимых атомов не остается постоянной, поскольку процесс излучения является случайным. Таким образом, волны испускаемые атомами, лишь короткий промежуток времени (порядка 10-8 с) имеют приблизительно постоянные амплитуду и фазы колебаний.
Проведенные рассуждения наталкивают на вывод о принципиальной невозможности получения интерференционной картины от естественного источника световой волны. Однако интерференционные картины все-таки наблюдаются. Для их существования необходимо выполнение ряда условий. Рассмотрим их.
|
|
|
Введем несколько понятий и определений. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом. Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга называется временем когерентности  . Когерентность существует только в пределах одного цуга и время когерентности не может превышать продолжительности излучения
. Когерентность существует только в пределах одного цуга и время когерентности не может превышать продолжительности излучения 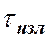 одного цуга, т.е.
одного цуга, т.е. 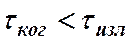 . Обнаружить четкую интерференционную картину можно только тогда, когда время разрешения прибора меньше времени когерентности накладываемых световых волн.
. Обнаружить четкую интерференционную картину можно только тогда, когда время разрешения прибора меньше времени когерентности накладываемых световых волн.
За время когерентности волна распространяется в вакууме на расстояние 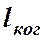 , равное
, равное 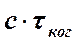 . Расстояние
. Расстояние 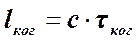 называется длиной когерентности (длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого одна или несколько световых волн утрачивают когерентность. Следовательно, для получения интерференционной картины разность хода световых волн должна быть меньше длины когерентности для используемого источника света:
называется длиной когерентности (длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого одна или несколько световых волн утрачивают когерентность. Следовательно, для получения интерференционной картины разность хода световых волн должна быть меньше длины когерентности для используемого источника света: 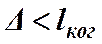 .
.
Длина когерентности световой волны непосредственно связана со степенью монохроматичности света, равной отношению 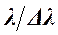 , где
, где 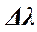 – конечный интервал длин волн, интерференция которых наблюдается. Эта связь выражается соотношением:
– конечный интервал длин волн, интерференция которых наблюдается. Эта связь выражается соотношением:
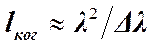 .
.
Таким образом, для получения интерференционной картины от реального источника излучения необходимо иметь излучение с малым значением 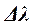 . Это условие представляет собой способ увеличения длины когерентности. Для солнечного света
. Это условие представляет собой способ увеличения длины когерентности. Для солнечного света 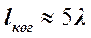 . Лазеры позволили получить
. Лазеры позволили получить 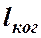 порядка сотен метров.
порядка сотен метров.
Рассмотрим для пояснения длины когерентности опыт Юнга.
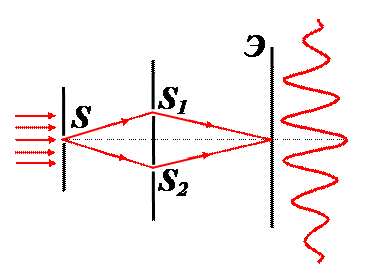 В опыте Юнга интерференционная картина по мере удаления от её середины размывается. Несколько полос видны, но далее постепенно они исчезают. Почему?
В опыте Юнга интерференционная картина по мере удаления от её середины размывается. Несколько полос видны, но далее постепенно они исчезают. Почему?
Ответ ясен: потому, что степень когерентности складываемых в этих точках экрана колебаний (волн) постепенно уменьшается, и, наконец, колебания становятся полностью некогерентными.
|
|
|
Исходя из этого факта, попытаемся объяснить наблюдаемое с помощью следующей модели. Пусть мы видим, например, первые четыре порядка интерференции (m = 4), а затем полосы исчезают. Этот переход наблюдается довольно плавным, но мы не будем останавливаться на деталях. Исчезновение полос с m > 4 означает, что колебания, пришедшие в соответствующие точки экрана от обеих волн, оказываются уже некогерентными между собой. Т.е. пока их разность хода не превышает m = 4 длин волн, колебания в какой-то степени когерентны. Значит, вдоль распространения волны когерентными между собой будут только участки волны в этом интервале длины. Данный интервал и называется длиной когерентности 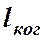 . В рассмотренном случае
. В рассмотренном случае 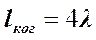 . Заметим, что в данных условиях это простейший способ оценки длины когерентности:
. Заметим, что в данных условиях это простейший способ оценки длины когерентности: 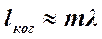 , где m –
, где m – 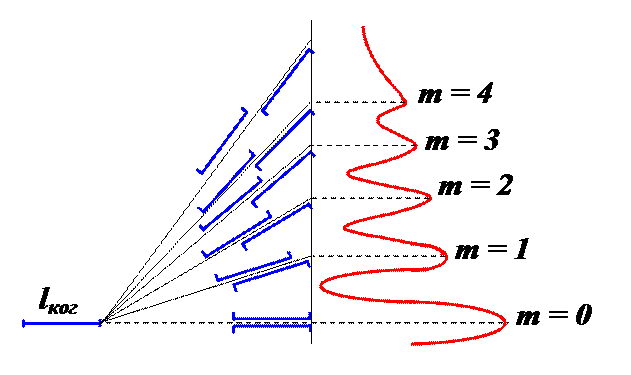
максимальный порядок интерференции, соответствующей ещё видимой полосе.
Всё это можно схематически представить с помощью рисунка.
В опыте Юнга, в падающие на обе щели волне длина когерентности равна 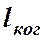 . Щели создают две волны с той же длиной когерентности, но поскольку они достигают разных точек экрана с различными разностями хода, то участки когерентности обеих волн постепенно сдвигаются относительно друг друга. Начиная с m = 5, они перестают перекрывать друг друга, т.е. складываемые колебания становятся некогерентными и интерференционные полосы исчезают.
. Щели создают две волны с той же длиной когерентности, но поскольку они достигают разных точек экрана с различными разностями хода, то участки когерентности обеих волн постепенно сдвигаются относительно друг друга. Начиная с m = 5, они перестают перекрывать друг друга, т.е. складываемые колебания становятся некогерентными и интерференционные полосы исчезают.
Всё сказанное, как мы увидим далее, справедливо при условии, что "первичная" щель S достаточно узкая. При расширении этой щели вступает в действие другой эффект. Рассмотрим его.
Вероятность возбуждения интерференционных колебаний, кроме временных параметров волн характеризуется также пространственной когерентностью. Эта характеристика связана с геометрическими размерами конкретной системы разделения световой волны и описывается так называемой шириной когерентности 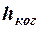 . Под шириной когерентности понимается расстояние между точками перпендикулярной к направлению распространения волны поверхности, в пределах которого волны когерентны.
. Под шириной когерентности понимается расстояние между точками перпендикулярной к направлению распространения волны поверхности, в пределах которого волны когерентны.
|
|
|
Как уже говорилось, цель в опыте Юнга предполагалась весьма узкой. Часто говорят о бесконечно узкой щели. Расширение же щели, как и уменьшение степени монохроматичности света приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению. Чтобы выяснить роль ширины щели S, рассмотрим теперь на примере опыта Юнга другой крайний случай: излучение монохроматическое, но щель не узкая.
Интерференционную картину на экране Э можно представить как наложение интерференционных картин от бесконечно узких щелей, на которые мысленно разобьем щель S. Пусть положение максимумов на экране Э от узкой щели, взятой около верхнего края щели S – точки 1 – таково, как отмечено сплошными отрезками на рисунке. А максимумы от узкой щели, взятой около нижнего края щели S – точки 2 – будут смещены вверх, они отмечены пунктирными отрезками на этом же рисунке. Интервалы между этими максимумами заполнены максимумами от промежуточных узких щелей, расположенных между краями 1 и 2.
При расширении щели S расстояния между максимумами от её крайних элементов будут увеличиваться, т.е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели.
Для простоты будем считать, что в приведённом рисунке расстояния a = c. Тогда при ширине щели b, равной ширине интерференционной полосы Dx, интервал между соседними максимумами от края 1 будет полностью заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.
Итак, при расширении щели S интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.
Это наблюдаемое явление можно объяснить иначе, а именно, интерференционная картина исчезает вследствие того, что вторичные источники – щели S1 и S2 становятся некогерентными. Сказанное позволяет говорить о ширине когерентности падающей на щели S1 и S2 световой волны – ширине  , на которой отдельные участки волны в достаточной степени когерентны между собой. Во избежание недоразумений уточним: под шириной
, на которой отдельные участки волны в достаточной степени когерентны между собой. Во избежание недоразумений уточним: под шириной 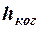 имеется в виду характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
имеется в виду характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
Ширина когерентности связана с длиной волны соотношением 
 ,
,
где 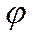 – угловая ширина источника относительно интересующего нас места (например, места разделения световой волны, экрана со щелями S1 и S2).
– угловая ширина источника относительно интересующего нас места (например, места разделения световой волны, экрана со щелями S1 и S2).
Это значит, что ширина когерентности пропорциональна длине волны и обратно пропорциональна угловой ширине источника.
|
|
|
Понятно, что для обеспечения пространственной когерентности освещения щелей S1 и S2 ширина b входной щели S должна быть достаточно малой.
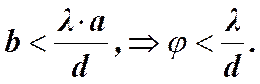
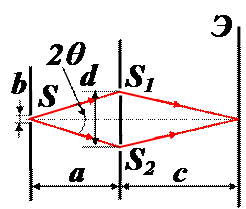 a – расстояние между экранами со щелями; j = b/a – угловой размер источника света – щели S.
a – расстояние между экранами со щелями; j = b/a – угловой размер источника света – щели S.
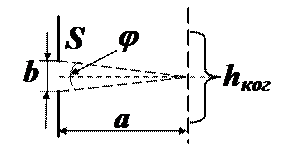
Интерференционная картина в монохроматическом свете с длиной волны l получается отчётливой, если выполняется следующее приближённое условие.
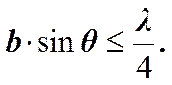
b – ширина щели S, а 2q - апертура интерференции.
Если в качестве источника использовать непосредственно Солнце (его угловой размер j» 0,01 рад и lср» 0,5 мкм), то ширина когерентности hког» 0,05 мм. Поэтому для получения интерференционной картины от двух щелей с помощью такого излучения расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.
Общие выводы. Для получения устойчивой интерференционной картины с использованием обычных источников света необходимо исходную световую волну разделить на две части, которые дадут интерференционную картину при соблюдении двух условий:
1. Разность хода световых волн должна быть меньше длины когерентности: 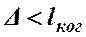 . Поскольку длина когерентности непосредственно зависит от монохроматичности волн и времени когерентности, это условие называется временной когерентностью волн.
. Поскольку длина когерентности непосредственно зависит от монохроматичности волн и времени когерентности, это условие называется временной когерентностью волн.
2. Ширина когерентности 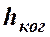 должна превышать расстояние между некоторыми характерными световыми лучами в месте расщепления исходной волны (на рисунках это расстояние
должна превышать расстояние между некоторыми характерными световыми лучами в месте расщепления исходной волны (на рисунках это расстояние 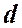 между источниками излучения
между источниками излучения  и
и 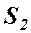 ).
).
|
|
|


