Интерференция, получаемая делением волнового фронта

Метод Юнга. Свет пропускается через узкую щель в непрозрачном экране и падает на две узкие щели и . Поскольку волны, исходящие из щелей и , получены делением одного и того же волнового фронта, исходящего из щели , то они являются когерентными и в области перекрытия этих световых пучков наблюдается интерференционная картина в виде чередующихся параллельных светлых и тёмных полос. В зависимости от разности хода до экрана происходит усиление или ослабление волн и на экране наблюдается чередование светлых и темных полос. Этот простейший опыт по интерференции света позволил Юнгу в 1802 году впервые объяснить результаты сложения световых пучков на основе волновых представлений.

Бипризма Френеля. В этой схеме для разделения исходной световой волны используют двойную призму Б (бипризму) с малым преломляющим углом (пси). Источником света служит ярко освещенная узкая щель , параллельная преломляющему ребру бипризмы. Поскольку преломляющий угол бипризмы очень мал (порядка десятка угловых минут), то все лучи отклоняются бипризмой на практически одинаковый угол . В результате образуются две когерентные волны, как бы исходящие из мнимых источников и , лежащих в одной плоскости со щелью 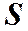. Наблюдаемая интерференционная картина имеет вид чередующихся параллельных светлых и тёмных полос.

Определим ширину интерференционной линии, используя записанную ранее формулу: , где 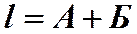- расстояние от источников до экрана. Учитывая, что расстояние между изображениями и щели равно , а , получим:

.

Видно, что ширина полос тем больше, чем больше расстояние от призмы до экрана.

Бизеркала Френеля. Здесь две когерентные световые волны получаются при отражении от двух зеркал, плоскости которых образуют небольшой угол a.

Источник света – узкая ярко освещённая щель S, параллельная линии пересечения зеркал. Отражённые от зеркал пучки падают на экран Э и там, где они перекрываются (зона интерференции), возникает интерференционная картина в виде полос, параллельных щели S. Отражённые от зеркал волны распространяются так, как если бы они исходили из мнимых источников S₁ и S₂, являющихся изображением щели S.

Ширина интерференционной полосы Dx на экране Э будет равна.

Видно, что ширина полос растёт с увеличением расстояния b. Если же на бизеркала падает плоская волна, т.е. a ® ¥, то имеем.

Т.е. ширина полос в этом случае не зависит от расстояния b – положения экрана.

Билинза Бийе. Обычную собирающую линзу разрезают пополам по диаметру, удаляя слой небольшой толщины, или обе половинки её сдвигают (или немного раздвигают). Такую систему называют билинзой. Рассмотрим билинзу, у которой толщина удалённого слоя равна d, а источник – ярко освещённая щель S расположен в плоскости, соединяющей обе половинки билинзы, и находится в её фокальной плоскости на расстоянии f от билинзы. В этом случае оптический центр O₁ верхней половинки 1 билинзы и оптический центр O₂ нижней половинки 2 расположены, как показано на рисунке. Расстояние между этими оптическими центрами равно толщине удалённого слоя d. Изобразив пунктиром побочные оптические оси, проходящие через щель S, и оптические центры обеих половинок билинзы, можно построить и ход лучей через эти половинки.

Таким образом, билинза расщепляет падающую на неё световую волну на две части, которые затем частично перекрываются (зона интерференции). На экране Э в области перекрытия волн возникает интерференционная картина в виде парабол. Ширина Dx интерференционной полосы будет равна.

Отсюда следует, что ширина полосы Dx в данном случае не зависит от расстояния между экраном и билинзой.