 |
Механизм возникновения синусоидальной ЭДС
|
|
|
|
Для исследования механизма возникновения и основных соотношений, характерных для синусоидальной ЭДС используем простейшую модель – рамку, вращающуюся с постоянной угловой скоростью ω в равномерном магнитном поле (рис. 1.3). Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции наводится ЭДС.
Рисунок 1.3
Значение ЭДС пропорционально магнитной индукции В, длине проводника l и скорости перемещения проводника относительно поля vt:
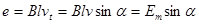. (1.8)
Угол α равен произведению угловой скорости рамки ω на время t:
.
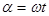Тогда ЭДС, возникающая в рамке, равна
. (1.9)
За один поворот рамки происходит полный цикл изменения ЭДС.
Частота вращения рамки n и частота ЭДС f связаны между собой соотношением
.
Откуда
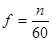. (1.10)
Действующие и средние значения периодических ЭДС и токов
Механическая сила взаимодействия двух проводников с одинаковыми токами и тепловое действие тока пропорциональны квадрату мгновенных значений тока. Если ток изменяется во времени, то тепловое или механическое действие определяется средним значением квадратов тока за полный цикл изменения, т.е. средним квадратичным значением тока. Поэтому для периодических переменных токов и ЭДС, значения которых повторяются через каждый период, введено понятие о действующих ЭДС и токах, являющихся средними квадратичными значениями этих величин. Действующий переменный ток, имеющий определенное значение, производит такое же механическое и тепловое действие, как и постоянный ток того же значения.
Количество теплоты, выделяемое постоянным током в резистивном элементе с активным сопротивлением за промежуток времени Т, равный периоду переменного тока, составляет
|
|
|
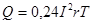. (1.11)
Количество теплоты, выделяемое переменным током в том же элементе за промежуток времени dt
. (1.12)
Количество теплоты, выделяемой за период,
. (1.13)
Приравнивая (1.11) и (1.13), имеем
. (1.14)
Тогда
. (1.15)
Аналогично для ЭДС и напряжений
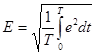; (1.16)
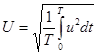. (1.17)
Выражения (1.15) – (1.17) определяют в общем виде действующие периодические токи, ЭДС и напряжения при любом законе их изменения.
Для синусоидального переменного тока 
:
. (1.18)
Второй интеграл равен нулю. тогда для действующего синусоидального тока имеем
. (1.19)
Аналогично для действующих синусоидальных ЭДС и напряжений
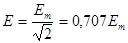; (1.20)
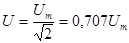. (1.21)
Почти все приборы, применяемые в электроизмерительной технике для измерения периодических напряжений и токов, регистрируют значения действующих напряжений и токов. Для этой цели шкалы приборов градуируются в соответствии с этими значениями.
Помимо действующих ЭДС и токов, в электротехнике рассматриваются и средние значения этих величин. Для синусоидальных ЭДС, токов и напряжений среднее значение за полный период равно нулю, т.к. площади отрицательных и положительных полуволн синусоид равны по величине и различны по знаку.
Для периодических величин, кривые которых симметричны относительно оси времени, принято определять среднее значение за положительный полупериод.
Среднее значение синусоидального тока
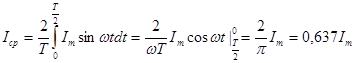. (1.22)
Средние значения ЭДС и напряжения:
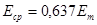; (1.23)
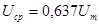. (1.24)
Синусоидальный ток в активном сопротивлении
Если по активному сопротивлению r протекает синусоидальный ток i = Im sin ωt, то в соответствии с законом Ома напряжение
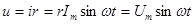. (1.25)
Мгновенная мощность
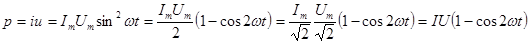. (1.26)
На рис. 4 приведены кривые мгновенных значений тока i, напряжения u и мощности р.
Мгновенная мощность имеет постоянную составляющую IU и составляющую IUcos2ωt, изменяющуюся с частотой 2ω. Потребляемая от источника питания за время dt энергия равна pdt.
|
|
|
Рисунок 1.4
|
|
|
