 |
Ценовая модель капитальных активов
|
|
|
|
Определение коэффициента бета (b)
Коэффициент бета вводится как одна из характеристик портфеля ценных бумаг. При использовании рыночного риска для оценки эффективности портфеля применяют апостериорную бету 
портфеля, полученную из следующих соображений.
Оценка эффективности портфеля проводится на основе сравнения характеристик портфеля с характеристиками рынка в целом. Пусть временной интервал, на котором оценивается эффективность портфеля, разбит на Т периодов. Например, если временной интервал равен 4 года, а период – кварталу, то Т =16. Средняя доходность портфеля за этот интервал времени вычисляется по формуле
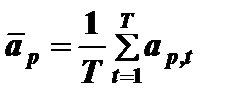, (7.13)
где t =1,2,... Т – номер периода; 
– доходность портфеля за период t.
Стандартное отклонение портфеля определяется выражением
(7.14)
Доходность портфеля сравнивается с доходностью аналогов рыночного портфеля, например, с индексом S&P500 (фондовый рыночный индекс Standard&Poors 500). S&P500 находится из средневзвешенной величины курсов акций 500 наиболее крупных компаний США.
Введем следующие обозначения: 
- доходность портфеля за период 
- доходность аналога рыночного портфеля за период t;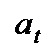 
- безрисковая ставка за период t; 
- избыточная доходность портфеля за период t; 
– избыточная доходность аналога рыночного портфеля за период 
. Полученные в результате анализа точки можно построить в прямоугольной декартовой системе координат, где по оси абсцисс откладываются значения избыточной доходности аналога рыночного портфеля 
, а по оси ординат – значения избыточной доходности портфеля 
(см. рис. 7.5).
Эти две переменные являются случайными величинами. В теории корреляционно-регрессионного анализа две такие переменные можно связать соотношением
|
|
|
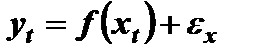, (7.15)
где 
– детерминированная функция регрессии от 
– возмущение в точке 
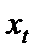, являющееся случайной величиной.
Рис. 7.5.
Обычно считают, что функция регрессии эффективности портфеля является линейной от эффективности рынка, то есть
; 
, (7.16)
где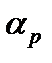 
– координата пересечения функции регрессии с осью 
, 
– бета портфеля (см. рис. 7.5). Если при 
, а угол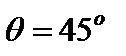 
, то характеристики портфеля в среднем соответствуют рыночным, а 
Коэффициенты уравнения регрессии определяются формулами
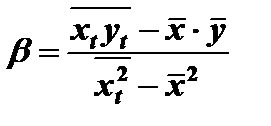(7.17)
, (7.18)
где
, (7.19)
, (7.20)
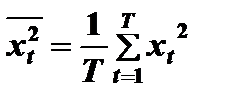(7.21)
Часто формулу для бета портфеля записывают в виде
, (7.22)
где 
– ковариация случайных величин 
и 
; 
– дисперсия случайной величины 
. Действительно, имеем следующие тождества
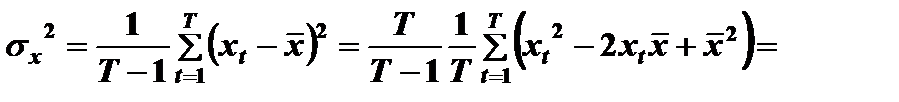
Подставив эти выражения в (7.22), получим (7.17).
Функцию средней доходности портфеля от бета портфеля найдем как среднее значение избыточной доходности портфеля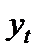 
, определяемое вторым уравнением (7.16)
Так как 
, (коэффициенты регрессии вычисляются методом наименьших квадратов),
, то
(7.23)
Эффективность управления портфелем может быть оценена с помощью апостериорной безопасной рыночной линии (Securily Market Line – SML). Для определения SML положим в (7.23) (эталонный портфель). Тогда
(7.24)
Вид апостериорной SML показан на рис. 7.6.
Рис. 7.6.
Одной из мер эффективности управления портфелем является разность между средней доходностью портфеля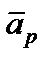 
(7. 23) и доходностью эталонного портфеля 
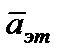(7. 24)
(7.25)
Величина 
называется апостериорной альфа.
Построение функции регрессии портфеля и определение разности между средней доходностью портфеля и доходностью эталонного портфеля 
проводится по следующему алгоритму:
- составляют таблицы периодических доходностей исследуемого портфеля, рыночного портфеля и безрискового актива;
- определяют бета и альфа портфеля по формулам (7.17) и (7.18);
- подставляя полученные значения в (7.16), строят функцию регрессии портфеля.
|
|
|
Пример 7.4. В табл. 7.7 приведены периодические значения доходностей за квартал в процентах исследуемого портфеля, рыночного портфеля и безрискового актива за 16 кварталов (4 года) [11]. Определить бета и альфа портфеля и построить функцию регрессии портфеля.
Решение. Средние доходности за квартал исследуемого портфеля, рыночного портфеля и безрискового актива равны
Таблица 7.7
| Номер квартала | ||||||||
Исследуемый портфель, 
| -8,77 | -6,03 | 14,14 | 24,96 | 3,71 | 10,65 | -0,22 | 0,27 |
Рыночный портфель, 
| -5,86 | -2,94 | 13,77 | 14,82 | 11,91 | 11,55 | -0,78 | 0,02 |
Безрисковый актив, 
| 2,97 | 3,06 | 2,85 | 1,88 | 1,9 | 2,22 | 2,11 |
Окончание табл. 7.7
| Номер квартала | Итого | ||||||||
Исследуемый портфель, 
| -3,08 | -6,72 | 8,58 | 1,15 | 7,87 | 5,92 | -3,1 | 13,61 | 62,94 |
Рыночный портфель, 
| -2,52 | -1,85 | 8,73 | 1,63 | 10,82 | 7,24 | -2,78 | 14,36 | 78,12 |
Безрисковый актив, 
| 2,16 | 2,34 | 2,44 | 2,4 | 1,89 | 1,94 | 1,72 | 1,75 | 35,63 |
Тогда зависимость апостериорной SML приобретает вид (рис. 7.7)
Рис. 7.7.
Средняя избыточная доходность за квартал исследуемого и рыночного портфелей равны
Результаты расчета 
приведены в табл. 7.8.
Таким образом,
Ковариация рыночного и исследуемого портфелей
Дисперсия рыночного портфеля
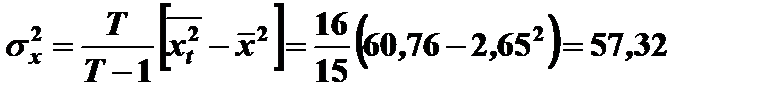
Таблица 7.8
| Квартал |  
| 
| 
| 
| 
|
| -11,74 | -8.83 | 137,83 | 77,97 | 103,66 | |
| -9,09 | -6 | 82,63 | 54,54 | ||
| 11,29 | 10,92 | 127,46 | 119,25 | 123,29 | |
| 23,08 | 12,94 | 532,69 | 167,44 | 298,66 | |
| 1,81 | 10,01 | 3,28 | 100,2 | 18,12 | |
| 8,65 | 9,55 | 74,82 | 91,2 | 82,61 | |
| -2,44 | -3 | 5.95 | 7,32 | ||
| -1,84 | -2,09 | 3,39 | 4,37 | 3,85 | |
| -5,24 | -4,68 | 27,46 | 21,9 | 24,52 | |
| -9,06 | -4,19 | 82,08 | 17,56 | 37,96 | |
| 6,14 | 6,29 | 37,7 | 39,56 | 38,62 | |
| -1,25 | -0,77 | 1,56 | 0,59 | 0,96 | |
| 5,98 | 8,93 | 35,76 | 79,74 | 53,4 | |
| 3,98 | 5,3 | 15,84 | 28,09 | 21,09 | |
| -4,82 | -4,5 | 23,23 | 20,25 | 21,69 | |
| 11,86 | 12,61 | 140,66 | 159,01 | 149,55 | |
| Итого | 27,31 | 42,49 | 1332,34 | 972,13 | 1039,84 |
Подставив эти значения в (7.22), получим
Известно, что средняя бета рыночного портфеля равна единице. Поскольку средняя бета исследуемого портфеля больше среднего бета рыночного портфеля, то можно сделать вывод о том, что менеджер исследуемого портфеля был относительно агрессивен.
Альфа портфеля может быть найдена по формуле (7.18)
%
Так как альфа портфеля отрицательна, то есть доходность исследуемого портфеля ниже доходности рыночного портфеля, то управление данным портфелем рассматривается как неэффективное.
|
|
|
Функция доходности исследуемого портфеля от коэффициента бета (7.23) имеет вид
Зависимость доходности исследуемого портфеля от бета портфеля представлена на рис. 7.7.
Функция регрессии портфеля имеет вид
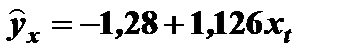
График этой функции представлен на рис. 7.8.
Рис. 7.8.
|
|
|
