 |
Факторы экономического роста
|
|
|
|
Основным фактором экономического роста станы в целом являются инвестиции [17-22].
Под экономическим ростом обычно понимают увеличение реального дохода в экономике, к которому относят Внутренний национальный продукт, Внутренний валовой продукт или Национальный доход, а также рост реального выпуска в расчете на душу населения.
Экономический рост называется экстенсивным, если он осуществляется за счет привлечения дополнительных ресурсов и не изменяет среднюю производительность труда. Интенсивный рост связан с применением более совершенных факторов производства и технологии, то есть осуществляется за счет роста отдачи от ресурсов.
Факторы экономического роста обычно группируются с типами экономического роста. К экстенсивным факторам относят рост затрат капитала и труда. К интенсивным факторам относят технологический прогресс, рост образовательного и профессионального уровня работников, совершенствование управления производством, улучшение законодательства и т.д.
Обычно экономический рост представляется в виде математических моделей, которые представляют собой упрощенное выражение реального экономического процесса в форме уравнений и графиков. Тем не менее экономическая модель дает возможность проанализировать отдельные стороны и закономерности экономического роста и управлять инвестициями так, что экономика будет развиваться оптимальным образом. Поэтому многие государства в качестве своей экономической политики выбирают ту или иную модель. В настоящее время широкое распространение получили кейнсианский и монетаристский подходы к прогнозированию и регулированию рыночной экономики.
Работа Кейнса "Общая теория занятости, процента и денег" вышла в 1936 г. как ответ на проблемы, возникшие в связи с кризисом перепроизводства и массовой безработицы в период Великой депрессии 1929–1933 гг. Кейнс видел свою задачу в том, чтобы показать, что равновесие при полной занятости не является общим случаем. Общий случай – это равновесие при наличии безработицы, а полная занятость лишь частный случай. Чтобы достигнуть желаемого состояния полной занятости, государство обязано проводить особую политику для ее достижения, поскольку автоматически действующие рыночные силы без этой поддержки не гарантируют ее достижения. При этом Дж. М. Кейнс считал, что деньги воздействуют на развитие экономики не через цены, а через норму ссудного процента. Рост нормы ссудного процента удорожает кредит и ведет к сокращению инвестиций в производство, а снижение нормы стимулирует инвестиции. Решающим рычагом воздействия на экономику Кейнс считал также налоговую политику и политику государственных расходов (фискальную политику). Облегчение налогового бремени и рост государственных инвестиций в экономику ускоряют темпы ее развития и наоборот. Кейнсианцы полагали, что денежная политика слабо влияет на развитие экономики в целом. В результате этого возник конфликт между монетаризмом и кейнсианством.
|
|
|
Коррекцией подхода Кейнса является монетаристский анализ экономики, развитый в начале 70-х годов 20 в. М. Фридманом. По мнению Фридмана главное влияние на движение основных макроэкономических показателей оказывает не спрос на товары, а контроль над предложением денег, а спрос на деньги не зависит от ставки процента. Монетаристы считают, что скорость обращения денег является величиной переменной, и денежно-кредитная политика имеет решающее значение в развитии экономики. Фридман сформулировал "денежное правило", по которому среднегодовой прирост денежной массы может составлять 4–5% в год при среднегодовом увеличении ВНП примерно на 3% и незначительном снижении скорости обращения денег. Это означает, что денежную массу следует наращивать с постоянным темпом независимо от динамики и циклических колебаний конъюнктуры рынка или ограничивать рост денежной массы постоянным темпом, но отнюдь не сокращать эту массу.
|
|
|
Считается, что при малой и контролируемой государством инфляции в своей политике государство должно использовать модель Кейнса, а при гиперинфляции и слабым ее контроле – модель Фридмана.
Модель Харрода-Домара
Наиболее простой кейнсианской моделью роста является модель Харрода-Домара. Модель описывает динамику дохода 
, который является суммой потребления 
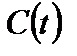и инвестиций 
(10.1)
Величина 
называется нормой накопления в момент времени 
.
Экономика считается закрытой, поэтому чистый экспорт равен нулю, а государственные расходы в модели не выделяются. Основной предпосылкой модели роста является формула взаимосвязи между инвестициями и скоростью роста дохода. Предполагается, что скорость роста дохода пропорциональна инвестициям, то есть
, (10.2)
где 
– коэффициент капиталоемкости прироста дохода. Обратная величина 
называется коэффициентом капиталоотдачи.
В модель включается ряд предпосылок.
1. Модель не учитывает выбытие основного капитала.
2. Инвестиционный лаг равен нулю, то есть инвестиции мгновенно переходят в прирост капитала. Это означает, что инвестиции 
за бесконечно малый отрезок времени 
равны приросту капитала 
, то есть 
или 
.
3. Подставив последнюю формулу в (12.2), найдем 
. Отсюда следует, что производственная функция модели линейна
,
причем в этой функции 
или 
, то есть затраты труда постоянны во времени либо выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом.
4. Модель не учитывает технического прогресса.
Подставив (10.2) в (10.1), получим дифференциальное уравнение модели
(10.3)
Соотношение (10.3) является линейным дифференциальным уравнением первого порядка. Обычно такие уравнения записывают в виде
(10.4)
Известно, что решение линейного дифференциального уравнения первого порядка 
можно представить в виде квадратур
|
|
|
Подставив обозначения (10.4) в последнюю формулу, получим
(10.5)
Пусть потребление в модели растет с постоянным темпом 
, то есть
Подставив выражение для потребления в (10.5), найдем
(10.6)
Постоянную интегрирования c определим, подставив в (10.6) t =0.
Отсюда получим
Подставив постоянную интегрирования в (10.6), получим
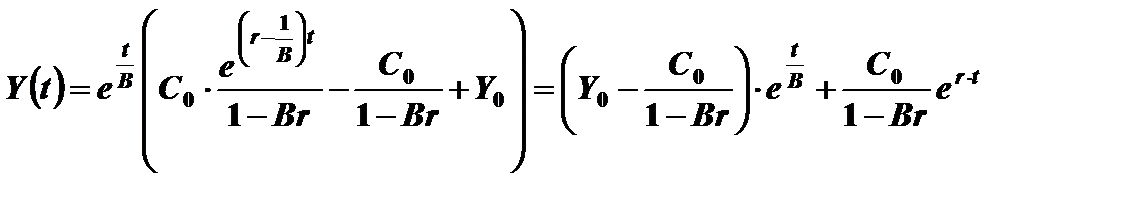(10.7)
Рассмотрим несколько частных случаев.
1. Пусть 
, то есть темп прироста потребления превышает коэффициент капиталоотдачи. Тогда второе слагаемое в (10.7), отвечающее за потребление становится отрицательным и, поскольку функция 
растет быстрее функции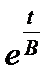 
, через некоторое время превысит по модулю первое. Таким образом, потребление будет занимать все большую часть дохода и в конце концов сведет к нулю сначала инвестиции, а затем доход.
2. Положим 
, то есть темп прироста потребления ниже коэффициента капиталоотдачи. В этом случае результат заметно зависит от нормы накопления в начальный момент времени 
и от соотношения
и 
(10.8)
2.1. Пусть 
. Тогда 
. Подставив это соотношение и (10.8) в формулу (10.7), получим
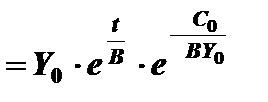
Отсюда следует, что темп прироста прямо пропорционален норме накопления в начальный момент времени и обратно пропорционален коэффициенту капиталоемкости.
2.2. Пусть 
. Тогда коэффициент в (10.7) при первом слагаемом
Поскольку в соотношении (10.7) коэффициент при показателе степени в первом слагаемом больше, чем во втором, то рано или поздно первое слагаемое по модулю превысит второе, и доход будет отрицательным.
2.3. Пусть 
. В этом случае при выполнении условия 
коэффициент в (10.7)
Поскольку также, как и в предыдущем случае, в соотношении (10.7) коэффициент при показателе степени в первом слагаемом больше, чем во втором, то рано или поздно первое слагаемое превысит второе. В дальнейшем первое слагаемое будет все более и более подавлять второе и процесс инвестирования будет вестись ради инвестирования, а не ради все большего удовлетворения потребностей людей.
Пример 10.1. Норма накопления в начальный момент времени составила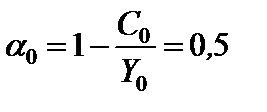 
, причем доход в начальный момент равняется 
. Провести исследование параметров модели при следующих условиях:
|
|
|
а) 
, 
, то есть 
.
б) 
, 
, то есть 
.
в) 
, 
, то есть 
.
г) 
, 
, то есть 
.
Решение. Потребление в начальный момент времени находим из соотношения 
, то есть 
.
а) функция дохода модели в зависимости от времени имеет вид
Потребление в модели изменяется по закону
Отсюда находим закон изменения инвестиций
Для определения момента времени, для которого инвестиции будут равны нулю, надо решить уравнение
,
, 
, 
, 
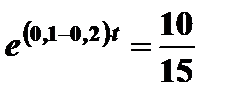года.
Таким образом, через четыре года инвестиции уменьшатся до нуля.
Момент времени, для которого доход будет равен нулю, находят из уравнения
,
, 
, 
, 
лет.
Через 11 лет до нуля уменьшится доход.
б ) находим траектории
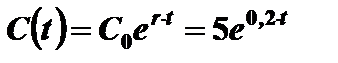
в) находим траектории
Определим моменты времени, для которых до нуля уменьшатся инвестиции и доход
, 
, 
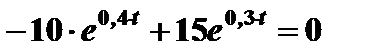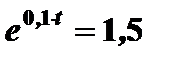года.
, 
, 
лет.
г) находим траектории
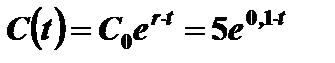
Полученные функции возрастают во времени.
Модель Солоу
Модель, предложенная лауреатом Нобелевской премии Р.Солоу, позволяет более точно описать некоторые особенности макроэкономических процессов за счет следующих особенностей:
- производственная функция в этой модели нелинейная,
- модель учитывает выбытие основного капитала,
- модель включает описание динамики трудовых ресурсов и технического прогресса и их влияния на экономический рост.
Состояние экономики в модели Солоу задается следующими пятью переменными, являющимися функциями времени, измеряемого в годах:
Y – внутренний валовой продукт;
C – потребление;
I – инвестиции;
L – число занятых в производстве (труд);
K – фонды (капитал).
На рис. 10.1 приведена схема функционирования экономики согласно модели Солоу. Здесь и далее используются обозначения:
– норма накопления, то есть доля валовых инвестиций в валовом внутреннем продукте,
– доля выбывших за год основных производственных фондов,
– годовой темп прироста числа занятых в производстве.
Рис. 10.1
Указанные параметры находятся в следующих границах:
, 
, 
.
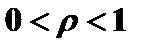Значения параметров , , 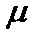постоянны во времени, причем норма накопления считается управляющим параметром, то есть в начальный момент времени может устанавливаться управляющим органом системы на любом уровне из области допустимых значений.
Предполагается, что выпуск в каждый момент времени определяется неоклассической производственной функцией 
, например, функцией Кобба-Дугласа
(10.9)
Изменение за небольшой промежуток времени согласно определению годового темпа прироста числа занятых в производстве определяются соотношением 
. Переходя к дифференциалам, получим 
. Решение этого дифференциального уравнения имеет вид 
, где 
– постоянная интегрирования. Отсюда находим 
. Значение 
находим при подстановке в последнюю формулу 
, то есть 
. Окончательно
|
|
|
Фонды за небольшой промежуток времени уменьшаются за счет их выбытия и увеличиваются за счет инвестиций. Их изменение за промежуток времени 
составит 
. Отсюда получаем дифференциальное уравнение 
с начальным условием 
.
Обобщим сказанное в виде модели Солоу в абсолютных показателях
; 
; 
; 
; 
; 
(10.10)
Введем удельные показатели:
– фондовооруженность;
народнохозяйственная производительность труда;
– удельные инвестиции на одного занятого;
– среднедушевое потребление на одного занятого.
Дифференциальное уравнение запишем в виде
; 
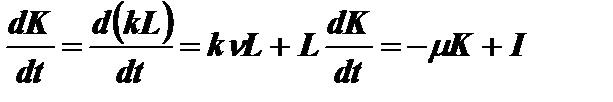Тогда в удельных показателях модель Солоу приобретает вид
; 
; 
; 
; 
; 
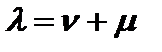(10.11)
Изменяющиеся во времени показатели, определяемые моделью (10.10) и (10.11), называются абсолютными или относительными траекториями. Траектория называется стационарной, если показатели не изменяются во времени, то есть
После выхода траектории на стационарный режим производная 
. Для этого режима дифференциальное уравнение принимает вид 
или
(10.12)
Поскольку функция 
– неоклассическая, то 
, 
, 
. Если задать условие 
, то уравнение (12.12) будет иметь единственное ненулевое решение 
(см рис.10.2). На рис. 10.2. введено обозначение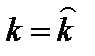 
, при котором скорости роста функций 
и 
равны. Значение 
является решением уравнения
(10.13)
Рис. 10.2
Если в начальный момент времени 
, то экономика находится на стационарной траектории и сойти с нее может только при изменении внешних условий, например, при изменении функции 
(переход к новым технологиям). При 
в экономике будет происходить переходной режим, который закончится установлением стационарного режима. Исследование переходного режима проведем для производственной функции Кобба-Дугласа (10.9). Для удельного внутреннего валового продукта имеем
(10.14)
Точку 
находят из уравнения
, 
, 
(10.15)
а точку 
– из уравнения
, 
, 
(10.16)
Дифференциальное уравнение (10.11) для производственной функции Кобба-Дугласа (10.14) приобретает вид
Введя замену 
, получим
или
Это уравнение с разделяющимися переменными
Его решение имеет вид
Постоянную интегрирования находим из условия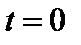 
, 
, 
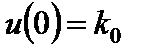
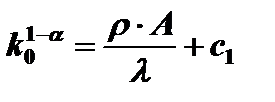Тогда
Подставив сюда 
(см. (10.15)), получим
.
Учитывая замену 
, найдем
(10.17)
Отсюда, в частности, имеем
Вид переходного процесса, определяемого траекторией (10.17), зависит от соотношения величин 
и 
. Первая производная фондовооруженности 
от времени, являющаяся исходным дифференциальным уравнением 
, будет положительной при возрастающей функции и отрицательной – при убывающей. Положив первую производную положительной, получим
, 
Учитывая, что 
, получим возрастающий переходной процесс при 
и убывающий при 
.
Проведем исследование функции (10.17) на наличие точки перегиба. Для этих целей определим вторую производную и приравняем ее нулю
Точка перегиба имеет место при
, 
Сопоставив это с (10.16), находим, что перегиб имеет место в точке
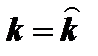
Таким образом, можно выделить три типа переходного процесса применительно к фондовооруженности (см. рис. 10.3).
1. 
. Вначале имеем ускоренный рост фондовооруженности, который при достижении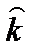 
сменяется замедленным ростом.
2. 
. Имеем замедленный рост фондовооруженности.
3. 
. Имеем замедляющееся падение фондовооруженности, то есть "проедание фондов".
Рис.10.3
Пример 10.2. Производственная функцией валового выпуска страны имеет вид 
. Валовой внутренний продукт и основные производственные фонды представлены в млрд. руб., а численность занятых в млн. чел. Норма накопления принимается равной 
, доля выбывших за год основных производственных фондов 
, годовой темп прироста числа занятых в производстве 
, удельная фондовооруженность в начальный момент времени 
. Определить удельную фондовооруженность 
на стационарной траектории и точку 
, народнохозяйственную производительность труда на стационарной траектории, удельные инвестиции на одного занятого на стационарной траектории, среднедушевое потребление на одного занятого на стационарной траектории и в начальный момент времени, а также время переходного процесса.
Решение. Удельный валовой внутренний продукт описывается уравнением
На стационарной траектории удельную фондовооруженность 
и точку 
находят из соотношений (10.15) и (10.16) при
Народнохозяйственная производительность труда на стационарной траектории
Удельные инвестиции на одного занятого на стационарной траектории
Среднедушевое потребление на одного занятого на стационарной траектории
Народнохозяйственная производительность труда в начальный момент времени
Среднедушевое потребление на одного занятого в начальный момент времени
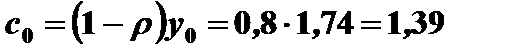
Траектория фондовооруженности определяется формулой (10.17) и при полученных данных может быть представлена в виде
Процесс считают установившимся при 
. Поэтому, подставив сюда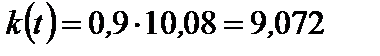 
, получим для 
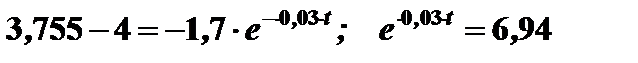
Решив это уравнение относительно 
, найдем время переходного процесса 
. Прологарифмировав правую и левую части последнего выражения, получим
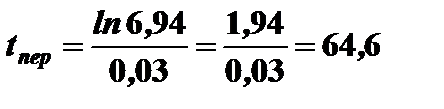лет.
10.4. "Золотое" правило накопления
Оптимальная норма накопления, соответствующая "золотому" правилу накопления Э. Фелпса, обеспечивает равновесный экономический рост с максимальным уровнем потребления.
На стационарной траектории функция удельного потребления при учете (12.14) и (12.15) может быть представлена в виде
Проведем исследование этой функции от норма накопления на экстремум. Для этого продифференцируем ее по норме накопления, приравняем производную нулю и решим уравнение
В точке 
имеет место максимум функции, так как левее этой точки производная положительна, то есть функция возрастает, а правее – отрицательна, то есть функция убывает. Таким образом, наибольшее потребление достигается при равенстве нормы накопления эластичности выпуска по фондам. На практике норма накопления всегда меньше оптимального значения, то есть имеет место недонакопление (рис. 10.4).
Рис. 10.4
В общем случае удельное потребление определяется соотношением
Установив 
, получим оптимальную траекторию удельного потребления
Начальное потребление в этом случае составит 
, а на стационарной траектории –
Если же 
, то начальное потребление будет равно 
, а на стационарной траектории –
Поскольку , то
, а 
, (10.18)
так как
(10.19)
Действительно, запишем (10.19) в виде
Пусть 
. Тогда последнее соотношение принимает вид
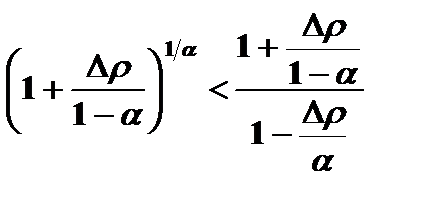
Разложим левую часть в ряд и ограничимся двумя первыми слагаемыми
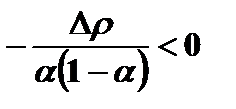
Таким образом, неравенства (10.18) и (10.19) имеют место. Траектории удельного потребления для 
и представлены на рис. 10.5. Из этого рисунка следует, что выигрыш в текущем потреблении приводит к проигрышу в ближайшей перспективе. В момент 
этого выигрыша уже не будет, а потом потребление будет меньше оптимального.
Пример 10.3. Условия примера 12.2. Норма накопления принимается равной 
.
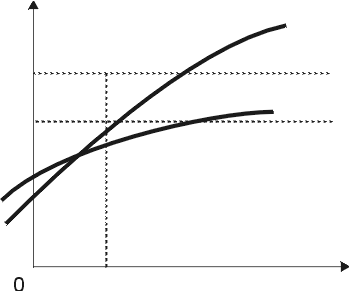
Рис. 10.5.
Решение. На стационарной траектории удельная фондовооруженность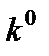 
и точка 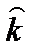равны
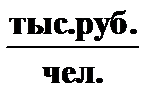
Народнохозяйственная производительность труда на стационарной траектории
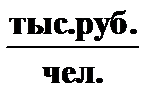
Удельные инвестиции на одного занятого на стационарной траектории
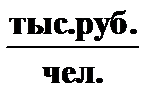
Среднедушевое потребление на одного занятого на стационарной траектории
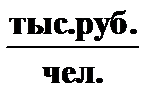
Народнохозяйственная производительность труда в начальный момент времени
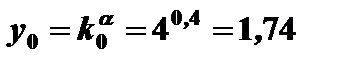
Среднедушевое потребление на одного занятого в начальный момент времени
Траектория фондовооруженности определяется формулой (10.17) и при полученных данных может быть представлена в виде
Подставив сюда 
, получим
Прологарифмировав, получим
лет.
Сопоставив полученные данные с данными примера 10.2, видим, что среднедушевое потребление на одного занятого в начальный момент времени уменьшилось на 
, а среднедушевое потребление на одного занятого на стационарной траектории увеличилось на 
. В то же время интервал выхода на стационарную траекторию увеличился с 64,6 года до 81,8 лет.
Контрольные вопросы
1.Дайте пояснения интенсивного и экстенсивного экономического роста.
2.В чем смысл кейнсианской и монетаристской моделей развития экономики?
3.Поясните модель развития экономики Харрода-Домара.
4.Перечислите основные предпосылки модели Солоу.
5.Начертите схему функционирования экономики согласно модели Солоу.
6.Дайте определение фондовооруженности, народнохозяйственной производительности труда, удельных инвестиций на одного занятого, среднедушевого потребления на одного занятого.
7.Опешите модель Солоу в абсолютных и удельных показателях.
8.Дайте определение траектории развития экономики.
9.Поясните графический метод определения фондовооруженности на стационарной траектории.
10.Поясните смысл входящих в формулу для траектории, полученной для производственной функции Кобба-Дугласа, величин.
11.Начертите траектории развития экономики для ускоренного роста фондовооруженности, замедленного роста фондовооруженности и для падения фондовооруженности.
12.Что называют оптимальной нормой накопления?
13.Начертите график удельного потребления от нормы накопления.
14.Как связан выигрыш в текущем потреблении с потреблением в перспективе?
Список литературы
1. Ильин Н. И. и др. Управление проектами. Санкт-Петербург: РАО "Газпром", 1996.
2. Идрисов А. Б. и др. Стратегическое планирование и анализ эффективности инвестиций. М.: ИИД "Филин", 1997.
3. Брейли Р., Майерс С. Принципы корпоративных финансов. М.: "Олимп-бизнес", 1997.
4. Бромвич М. Анализ экономической эффективности капиталовложений. М.: ИНФРА-М, 1996.
5. Ильенкова С. Д. Инновационный менеджмент. М.: ЮНИ
|
|
|
