 |
Назначение основных теорем. Сумма и произведение событий
|
|
|
|
В предыдущей главе мы познакомились со способами непосредственного определения вероятностей, а именно: с классической формулой для вероятности события, сводящегося к схеме случаев, и со способом приближенного определения вероятности по частоте для события, которое к схеме случаев не сводится. Однако не эти непосредственные способы являются основными в теории вероятностей: их применение не всегда удобно и не всегда возможно. Даже когда событие сводится к схеме случаев, зачастую эта схема бывает слишком сложна, и непосредственный подсчет вероятности по формуле (2.2.1) становится чрезмерно громоздким. Что касается событий, не сводящихся к схеме случаев, то и их вероятности лишь в редких случаях определяются непосредственно по частотам. На практике обычно требуется определять вероятности событий, непосредственное экспериментальное воспроизведение которых затруднено. Например, если требуется определить вероятностьпоражения самолета в воздушном бою, ясно, что определение этой вероятности по частоте практически невозможно. И не только потому, что такие опыты оказались бы непомерно сложными и дорогостоящими, а еще и потому, что часто нам требуется оценить вероятность того или иного исхода боя не для существующих образцов техники, а для перспективных, проектируемых. Обычно такая оценка и производится для того, чтобы выявить наиболее рациональные конструктивные параметры элементов перспективной техники.
Поэтому, как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Вся теория вероятностей, в основном, и представляет собой систему таких косвенных методов, пользование которыми позволяет свести необходимый эксперимент к минимуму.
|
|
|
Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными теоремамитеории вероятностей. Этих теорем две: теорема сложения вероятностей и теорема умножения вероятностей. Строго говоря, оба эти положения являются теоремами и могут быть доказаны только для событий, сводящихся к схеме случаев. Для событий, не сводящихся к схеме случаев, они принимаются аксиоматически, как принципы или постулаты.
Перед тем, как формулировать и доказывать основные теоремы, введем некоторые вспомогательные понятия, а именно понятия о сумме событий и произведении событий.
Во многих областях точных наук применяются символические операции над различными объектами, которые получают свои названия по аналогии с арифметическими действиями, рядом свойств которых они обладают. Таковы, например, операции сложения и умножения векторов в механике, операции сложения и умножения матрицв алгебре и т.д. Эти операции, подчиненные известным правилам, позволяют не только упростить форму записей, но в ряде случаев существенно облегчают логическое построение научных выводов. Введение таких символических операций над событиями оказывается плодотворным и в теории вероятностей.
Суммой двух событий  и
и  называется событие
называется событие  , состоящее в выполнении события
, состоящее в выполнении события  или события
или события  , или обоих вместе.
, или обоих вместе.
Например, если событие  – попадание в цель при первом выстреле, событие
– попадание в цель при первом выстреле, событие  – попадание в цель при втором выстреле, то событие
– попадание в цель при втором выстреле, то событие  есть попадание в цель вообще, безразлично при каком выстреле – при первом, при втором или при обоих вместе.
есть попадание в цель вообще, безразлично при каком выстреле – при первом, при втором или при обоих вместе.
Если события  и
и  несовместимы, то естественно, что появление этих событий вместе отпадает, и сумма событий
несовместимы, то естественно, что появление этих событий вместе отпадает, и сумма событий  и
и  сводится к появлению или события
сводится к появлению или события  , или события
, или события  . Например, если событие
. Например, если событие  – появление карты червонной масти при вынимании карты из колоды, событие
– появление карты червонной масти при вынимании карты из колоды, событие  – появление карты бубновой масти, то
– появление карты бубновой масти, то  есть появление карты красной масти, безразлично – червонной или бубновой.
есть появление карты красной масти, безразлично – червонной или бубновой.
|
|
|
Короче, суммой двух событий  и
и  называется событие
называется событие  , состоящее в появлении хотя бы одного из событий
, состоящее в появлении хотя бы одного из событий  и
и  .
.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Например, если опыт состоит в пяти выстрелах по мишени и даны события:
 – ни одного попадания,
– ни одного попадания,
 – ровно одно попадание,
– ровно одно попадание,
 – ровно два попадания,
– ровно два попадания,
 - ровно три попадания,
- ровно три попадания,
 – ровно четыре попадания,
– ровно четыре попадания,
 – ровно пять попаданий,
– ровно пять попаданий,
то

есть событие «не более двух попаданий», а

есть событие «не менее трех попаданий».
Произведением двух событий  и
и  называется событие
называется событие  , состоящее в совместном выполнении события
, состоящее в совместном выполнении события  и события
и события  .
.
Например, если событие  – появление туза при вынимании карты из колоды, событие
– появление туза при вынимании карты из колоды, событие  – появление карты бубновой масти, то событие
– появление карты бубновой масти, то событие  есть появление бубнового туза. Если производится два выстрела по мишени и событие
есть появление бубнового туза. Если производится два выстрела по мишени и событие  – попадание при первом выстреле, событие
– попадание при первом выстреле, событие  – попадание при втором выстреле, то
– попадание при втором выстреле, то  есть попадание при обоих выстрелах.
есть попадание при обоих выстрелах.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Например, если по мишени производится три выстрела, и рассматриваются события
 – промах при первом выстреле,
– промах при первом выстреле,
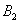 – промах при втором выстреле,
– промах при втором выстреле,
 - промах при третьем выстреле,
- промах при третьем выстреле,
то событие

состоит в том, что в мишень не будет ни одного попадания.
При определении вероятностей часто приходится представлять сложные события в виде комбинаций более простых событий, применяя и операцию сложения, и операцию умножения событий.
Например, пусть по мишени производится три выстрела, и рассматриваются следующие элементарные события:
 - попадание при первом выстреле,
- попадание при первом выстреле,
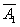 - промах при первом выстреле,
- промах при первом выстреле,
 - попадание при втором выстреле,
- попадание при втором выстреле,
 - промах при втором выстреле,
- промах при втором выстреле,
 - попадание при третьем выстреле,
- попадание при третьем выстреле,
 - промах при третьем выстреле.
- промах при третьем выстреле.
Рассмотрим более сложное событие  , состоящее в том, что в результате данных трех выстрелов будет ровно одно попадание в мишень. Событие
, состоящее в том, что в результате данных трех выстрелов будет ровно одно попадание в мишень. Событие  можно представить в виде следующей комбинации элементарных событий:
можно представить в виде следующей комбинации элементарных событий:
|
|
|
 .
.
Событие  , состоящее в том, что в мишень будет не менее двух попаданий, может быть представлено в виде:
, состоящее в том, что в мишень будет не менее двух попаданий, может быть представлено в виде:
 .
.
Такие приемы представления сложных событий часто применяются в теории вероятностей.
Непосредственно из определения суммы и произведения событий следует, что

Если событие  есть частный случай события
есть частный случай события  , то
, то

При пользовании понятиями суммы и произведения событий часто оказывается полезной наглядная геометрическая интерпретация этих понятий.

Рис. 3.1.1.

Рис. 3.1.2.
На рис. 3.1.1 наглядно иллюстрированы понятия суммы и произведения двух событий. Если событие  есть попадание точки в область
есть попадание точки в область  , соответственно событие
, соответственно событие  – попадание в область
– попадание в область  , то событие
, то событие 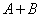 есть попадание в область, заштрихованную на рис. 3.1.1, а), а событие
есть попадание в область, заштрихованную на рис. 3.1.1, а), а событие  – в область, заштрихованную на рис. 3.1.1, б). На рис. 3.1.2 аналогично показаны сумма и произведение трех событий.
– в область, заштрихованную на рис. 3.1.1, б). На рис. 3.1.2 аналогично показаны сумма и произведение трех событий.
|
|
|


