 |
Теорема гипотез (формула Бейеса)
|
|
|
|
Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез, или формула Бейеса.
Поставим следующую задачу.
Имеется полная группа несовместных гипотез 
. Вероятности этих гипотез до опыта известны и равны соответственно 
. Произведен опыт, в результате которого наблюдено появление некоторого события 
. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события?
Здесь, по существу, речь идет о том, чтобы найти условную вероятность 
для каждой гипотезы.
Из теоремы умножения имеем:
,
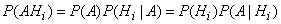
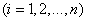или, отбрасывая левую часть,
,
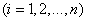откуда
.
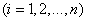Выражая 
с помощью формулы полной вероятности (3.4.1), имеем:
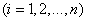. (3.5.1)
Формула (3.5.1) и носит название формулы Бейеса или теоремы гипотез.
Пример 1. Прибор может собираться из высококачественных деталей и из деталей обычного качества; вообще около 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время 
равна 0,95; если из деталей обычного качества – его надежность равна 0,7. Прибор испытывался в течение времени и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.
Решение. Возможны две гипотезы:
- прибор собран из высококачественных деталей,
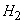- прибор собран из деталей обычного качества.
Вероятность этих гипотез до опыта:
.
В результате опыта наблюдено событие – прибор безотказно работал время .
Условные вероятности этого события при гипотезах и 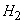равны:
По формуле (3.5.1) находим вероятность гипотезы после опыта:
.
Пример 2. Два стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.
|
|
|
Решение. До опыта возможны следующие гипотезы:
- ни первый, ни второй стрелок не попадет,
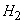- оба стрелка попадут,
- первый стрелок попадет, а второй нет,
- первый стрелок не попадет, а второй попадет.
Вероятность этих гипотез:
Условные вероятности наблюденного события при этих гипотезах равны:
После опыта гипотезы и 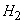становятся невозможными, а вероятности гипотез и будут равны:
Следовательно, вероятность того, что пробоина принадлежит первому стрелку, равна 
.
Пример 3. Производится наблюдение за некоторым объектом с помощью двух наблюдательных станций. Объект может находиться в двух различных состояниях 
и 
, случайно переходя из одного в другое. Долговременной практикой установлено, что примерно 30% времени объект находится в состоянии , а 70% - в состоянии . Наблюдательная станция №1 передает ошибочные сведения приблизительно в 2% всех случаев, а наблюдательная станция №2 – в 8%. В какой-то момент времени наблюдательная станция №1 сообщила: объект находится в состоянии , а наблюдательная станция №2: объект находится в состоянии .
Спрашивается: какому из сообщений верить?
Решение. Естественно, верить тому из сообщений, для которого больше вероятность того, что оно соответствует истине. Применим формулу Бейеса. Для этого сделаем гипотезы о состоянии объекта:
- объект находится в состоянии ,
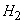- объект находится в состоянии .
Наблюденное событие состоит в следующем: станция №1 сообщила, что объект находится в состоянии , а станция №2 – что он находится в состоянии . Вероятности гипотез до опыта
Найдем условные вероятности наблюденного события при этих гипотезах. При гипотезе чтобы произошло событие , нужно, чтобы первая станция передала верное сообщение, а вторая – ошибочное:
|
|
|
.
Аналогично
.
Применяя формулу Бейеса, найдем вероятность того, что истинное состояние объекта - :
,
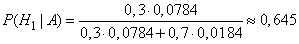т.е. из двух сообщений более правдоподобным является сообщение первой станции.
ГЛАВА 4 ПОВТОРЕНИЕ ОПЫТОВ
|
|
|
