Главная | Обратная связь | Поможем написать вашу работу!

Теорема умножения вероятностей

Перед тем, как излагать теорему умножения вероятностей, введем еще одно важное понятие: понятие о независимых и зависимых событиях.

Событие называется независимым от события , если вероятность события не зависит от того, произошло событие или нет.

Событие называется зависимым от события , если вероятность события А меняется в зависимости от того, произошло событие или нет.

Рассмотрим примеры.

1) Опыт состоит в бросании двух монет; рассматриваются события:

– появление герба на первой монете,

– появление герба на второй монете.

В данном случае вероятность события не зависит от того, произошло событие или нет; событие независимо от события .

2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:

– появление белого шара у 1-го лица,

– появление белого шара у 2-го лица.

Вероятность события до того, как известно что-либо о событии , равна 2/3. Если стало известно, что событие произошло, то вероятность события становится равной ½, из чего заключаем, что событие зависит от события .

Вероятность события , вычисленная при условии, что имело место другое событие , называется условнойвероятностью события и обозначается

Для условий последнего примера

; .

Условие независимости события от события можно записать в виде:

а условие зависимости – в виде:

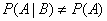Перейдем к формулировке и доказательству теоремы умножения вероятностей.

Теорема умножения вероятностей формулируется следующим образом.

Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятностьдругого, вычисленную при условии, что первое имело место:

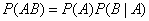. (3.3.1)

Докажем теорему умножения для схемы случаев. Пусть возможные исходы опыта сводятся к случаям, которые мы снова для наглядности изобразим в виде точек:

Предположим, что событию благоприятны случаев, а событию благоприятны случаев. Так как мы не предполагали события и несовместными, то вообще существуют случаи, благоприятные и событию , и событию одновременно. Пусть число таких случаев . Тогда

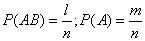Вычислим , т.е. условную вероятность события в предположении, что имело место. Если известно, что событие произошло, то из ранее возможных случаев остаются возможными только те , которые благоприятствовали событию . Из них случаев благоприятны событию . Следовательно,

Подставляя выражения и в формулу (3.3.1), получим тождество. Теорема доказана.

Очевидно, при применении теоремы умножения вполне безразлично, какое из событий и считать первым, а какое вторым, и теорему умножения можно записать в таком виде:

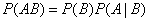Отметим следствия, вытекающие из теоремы умножения.

Следствие 1. Если событие не зависит от события , то и событие не зависит от события .

Доказательство. Дано, что событие не зависит от , т.е.

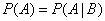. (3.3.2)

Требуется доказать, что и событие не зависит от , т.е.

При доказательстве будем предполагать, что .

Напишем теорему вероятности в двух формах:

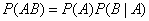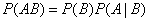откуда

или, согласно условию (3.3.2),

. (3.3.3)

Разделим обе части равенства (3.3.3) на . Получим:

что и требовалось доказать.

Из следствия 1 вытекает, что зависимость или независимость событий всегда взаимны. В связи с этим модно дать следующее новое определение независимых событий.

Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Следствие непосредственно вытекает из определения независимых событий.

Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется так.

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

. (3.3.4)

Доказательство может быть дано тем же методом полной индукции.

В случае независимых событий теорема упрощается и принимает вид:

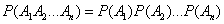, (3.3.5)

т.е. вероятность произведения независимых событий равна произведению вероятностей этих событий.

Применяя знак произведения, теорему можно записать в виде:

. (3.3.6)

Рассмотрим примеры на применение теоремы умножения вероятностей.

Пример 1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Решение. Обозначим:

- появление двух белых шаров.

Событие представляет собой произведение двух событий:

где - появление белого шара при первом вынимании, - появление белого шара при втором вынимании.

По теореме умножения вероятностей

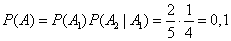Пример 2. Те же условия, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются.

Решение. В данном случае события и независимы и

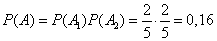Пример 3. Прибор, работающий в течение времени , состоит из трех узлов, каждый из которых, независимо от других, может в течение времени отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время надежность (вероятность безотказной работы) первого узла равна ; второго ; третьего . Найти надежность прибора в целом.

Решение. Обозначая:

– безотказная работа приборов,

- безотказная работа первого узла,

- безотказная работа второго узла,

- безотказная работа третьего узла,

имеем:

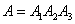откуда по теореме умножения для независимых событий

На практике сравнительно редко встречаются задачи, в которых нужно применять только теорему сложения или только теорему умножения вероятностей. Обычно обе теоремы приходиться применять совместно. При этом, как правило, событие, вероятность которого требуется определить, представляется в виде суммы нескольких несовместных событий (вариантов данного события), каждое из которых в свою очередь являетсяпроизведением событий.

Пример 4. Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно

Найти вероятность того, что в результате этих трех выстрелов в мишени будет ровно одна пробоина.

Решение. Рассмотрим событие – ровно одно попадание в мишень. Это событие может осуществиться несколькими способами, т.е. распадается на несколько несовместных вариантов: может быть попадание при первом выстреле, промахи при втором и третьем; или же попадание при втором выстреле, промахи при первом и третьем; или, наконец, промахи при первом и втором выстрелах и попадание при третьем. Следовательно,

где - попадание при первом, втором, третьем выстрелах, - промах при первом, втором, третьем выстрелах.

Применяя теоремы сложения и умножения вероятностей и пользуясь свойством противоположных событий, находим:

Пример 5. В условиях предыдущего примера найти вероятность того, что в мишени будет хотя бы одна пробоина.

Решение. Рассмотрим событие – хотя бы одно попадание в мишень. Пользуясь тем же приемом, который был применен в предыдущем примере, и теми же обозначениями, можно представить событие в виде суммы несовместных вариантов:

найти вероятность каждого варианта по теореме умножения и все эти вероятности сложить. Однако такой путь решения задачи слишком сложен; здесь целесообразно от прямого события перейти к противоположному:

- ни одного попадания в мишень.

Очевидно,

По теореме умножения

откуда

На последнем примере проиллюстрирован принцип целесообразности применения противоположных событий втеории вероятностей. Его можно сформулировать следующим образом.

Если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию.

Пример 6. Происходит бой («дуэль») между двумя участниками (летательными аппаратами, танками, кораблями) и . У стороны в запасе два выстрела, у стороны – один. Начинает стрельбу : он делает по один выстрел и поражает его с вероятностью 0,2. Если не поражен, он отвечает противнику выстрелом и поражает его с вероятностью 0,3. Если этим выстрелом не поражен, то он делает по свой последний выстрел, которым поражает его с вероятностью 0,4. Найти вероятность того, что в бою будет поражен: а) участник , б) участник .

Решение. Рассмотрим события:

– поражение участника ,

– поражение участника .

Для выполнения события необходимо совмещение (произведение) двух событий: 1) не поразил первым выстрелом и 2) поразил а своим ответным выстрелом. По теореме умножения вероятностей получим

Перейдем к событию . Оно, очевидно, состоит из двух несовместных вариантов:

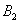где - поражение участника первым выстрелом , - поражение участника вторым выстрелом .

По теореме сложения вероятностей

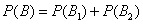По условию =0,2. Что касается события 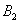, то оно представляет собой совмещение (произведение) трех событий, а именно:

1) первый выстрел стороны не должен поразить ;

2) ответный выстрел стороны не должен поразить ;

3) последний (второй) выстрел стороны должен поразить .

По теореме умножения вероятностей

откуда

Пример 7. Цель, по которой ведется стрельба, состоит из трех различных по уязвимости частей. Для поражения цели достаточно одного попадания в первую часть, или двух попаданий во вторую, или трех попаданий в третью. Если снаряд попал в цель, то вероятность ему попасть в ту или другую часть пропорциональна площади этой части. На проекции цели на плоскость, перпендикулярную направлению стрельбы, первая, вторая и третья части занимают относительные площади 0,1, 0,2 и 0,7. Известно, что в цель попало ровно два снаряда. Найти вероятность того, что цель будет поражена.

Решение. Обозначим – поражение цели; - условную вероятность поражения цели при условии, что в нее попали ровно два снаряда. Два снаряда, попавшие в цель, могут поразить её двумя способами: или хотя бы один из них попадает в первую часть, или же оба снаряда попадут во вторую. Эти варианты несовместны, так как в цель попало всего два снаряда; поэтому можно применить теорему сложения. Вероятность того, что хотя бы один снаряд попадет в первую часть, может быть вычислена через вероятность противоположного события (ни один из двух снарядов не попадет в первую часть) и равна . Вероятность того, что оба снаряда попадут во вторую часть, равна . Следовательно,

Пример 8. Для условий предыдущего примера найти вероятность поражения цели, если известно, что в нее попало три снаряда.

Решение. Решим задачу двумя способами: через прямое и противоположное событие.

Прямое событие – поражение цели при трех попаданиях – распадается на четыре несовместных варианта:

– хотя бы одно попадание в первую часть,

– два попадания во вторую часть и одно – в третью,

- три попадания во вторую часть,

– три попадания в третью часть.

Вероятность первого варианта находим аналогично предыдущему примеру:

Найдем вероятность второго варианта. Три попавших снаряда могут распределиться по второй и третьей частям нужным образом (два во вторую и один – в третью) тремя способами (). Следовательно,

Далее находим:

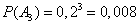Отсюда

Однако проще решается задача, если перейти к противоположному событию – непоражению цели при трех попаданиях. Это событие может осуществиться только одним способом: если два снаряда из трех попадут в третью часть, а один – во вторую. Таких комбинаций может быть три (), следовательно,

откуда

Пример 9. Монета бросается 6 раз. Найти вероятность того, что выпадет больше гербов, чем цифр.

Решение. Для нахождения вероятности интересующего нас события (выпадет больше гербов, чем цифр) можно было бы перечислить все возможные его варианты, например:

– выпадет шесть гербов и ни одной цифры,

– выпадет пять гербов и одна цифра

и т.д.

Однако проще будет применить другой прием. Перечислим все возможные исходы опыта:

– выпадет больше гербов, чем цифр,

– выпадет больше цифр, чем гербов,

– выпадет одинаковое число цифр и гербов.

События , , несовместны и образуют полную группу. Следовательно,

Так как задача симметрична относительно «герба» и «цифры»,

откуда

Найдем вероятность события , состоящего в том, что при шести бросаниях монеты появится ровно три герба (а, значит, ровно три цифры). Вероятность любого из вариантов события (например, последовательности г, ц, г, г, ц, ц при шести бросаниях) одна и та же и равна . Число таких комбинаций равно (числу способов, какими можно из шести бросаний выбрать три, в которых появился герб). Следовательно,

;

отсюда

Пример 10. Прибор состоит из четырех узлов: 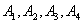, причем узел дублирует узел , а узел дублирует узел . При отказе (выходе из строя) любого из основных узлов ( или ) происходит автоматическое переключение на дублирующий узел. Надежность (вероятность безотказной работы) в течение заданного времени каждого из узлов равна соответственно . Надежность каждого из переключающих устройств равна . Все элементы выходят из строя независимо друг от друга. Определить надежность прибора.

Решение. Рассмотрим совокупность узлов и соответствующего переключающего устройства как один «обобщенный узел» , а совокупность узлов и соответствующего обобщающего устройства – как обобщенный узел . Рассмотрим события: