 |
Характеристики положения (математическое ожидание, мода, медиана)
|
|
|
|
Среди числовых характеристик случайных величин нужно, прежде всего, отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.
Среднее значение случайной величины есть некоторое число, являющееся как бы её «представителем» и заменяющее её при грубо ориентировочных расчетах. Когда мы говорим: «среднее время работы лампы равно 100 часам» или «средняя точка попадания смещена относительно цели на 2 м вправо», мы этим указываем определенную числовую характеристику случайной величины, описывающую её местоположение на числовой оси, т.е. «характеристику положения».
Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожиданиеслучайной величины, которое иногда называют просто средним значением случайной величины.
Рассмотрим дискретную случайную величину 
, имеющую возможные значения 
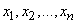с вероятностями 
. Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым «средним взвешенным» из значений 
, причем каждое значение при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднееслучайной величины , которое мы обозначим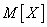 
:
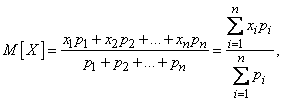
или, учитывая, что 
,
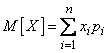. (5.6.1)
Это среднее взвешенное значение и называется математическим ожиданием случайной величины. Таким образом, мы ввели в рассмотрении одно из важнейших понятий теории вероятностей – понятие математического ожидания.
|
|
|
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Заметим, что в вышеприведенной формулировке определение математического ожидания справедливо, строго говоря, только для дискретных случайных величин; ниже будет дано обобщение этого понятия на случай непрерывных величин.
Для того, чтобы сделать понятие математического ожидания более наглядным, обратимся к механической интерпретации распределения дискретной случайной величины. Пусть на оси абсцисс расположены точки с абсциссами 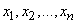, в которых сосредоточены соответственно массы , причем . Тогда, очевидно, математическое ожидание 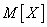, определяемое формулой (5.6.1), есть не что иное, как абсцисса центра тяжести данной системы материальных точек.
Математическое ожидание случайной величины связано своеобразной зависимостью со средним арифметическим наблюденных значений случайной величины при большом числе опытов. Эта зависимость того же типа, как зависимость между частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к еематематическому ожиданию. Из наличия связи между частотой и вероятностью можно вывести как следствие наличие подобной же связи между средним арифметическим и математическим ожидание.
Действительно, рассмотрим дискретную случайную величину , характеризуемую рядом распределения:
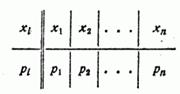
где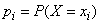 
.
Пусть производится 
независимых опытов, в каждом из которых величина принимает определенное значение. Предположим, что значение 
появилось 
раз, значение 
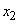появилось 
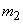раз, вообще значение появилось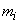 
раз. Очевидно,
Вычислим среднее арифметическое наблюденных значений величины , которое, в отличие отматематического ожидания 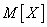мы обозначим 
:
|
|
|
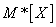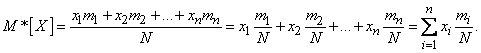
Но 
есть не что иное, как частота (или статистическая вероятность) события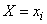 
; эту частоту можно обозначить 
. Тогда
,
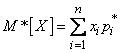т.е. среднее арифметическое наблюденных значений случайной величины равно сумме произведений всех возможных значений случайной величины на частоты этих значений.
При увеличении числа опытов частоты будут приближаться (сходиться по вероятности) к соответствующим вероятностям 
. Следовательно, и среднее арифметическое наблюденных значений случайной величины 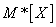при увеличении числа опытов будет приближаться (сходится по вероятности) к её математическому ожиданию .
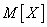Сформулированная выше связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел. Строгое доказательство этого закона будет дано нами в главе 13.
Мы уже знаем, что все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Здесь речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно; при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается кпостоянной величине – математическому ожиданию.
Свойство устойчивости средних при большом числе опытов легко проверить экспериментально. Например, взвешивая какое-либо тело в лаборатории на точных весах, мы в результате взвешивания получаем каждый раз новое значение; чтобы уменьшить ошибку наблюдения, мы взвешиваем тело несколько раз и пользуемся средним арифметическим полученных значений. Легко убедиться, что при дальнейшем увеличении числа опытов (взвешиваний) среднее арифметическое реагирует на это увеличение все меньше и меньше и при достаточно большом числе опытов практически перестает меняться.
Формула (5.6.1) для математического ожидания соответствует случаю дискретной случайной величины. Для непрерывной величины математическое ожидание, естественно, выражается уже не суммой, а интегралом:
, (5.6.2)
где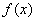 
- плотность распределения величины .
Формула (5.6.2) получается из формулы (5.6.1), если в ней заменить отдельные значения непрерывно изменяющимся параметром х, соответствующие вероятности - элементом вероятности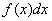 
, конечную сумму – интегралом. В дальнейшем мы часто будем пользоваться таким способом распространения формул, выведенных для прерывных величин, на случай непрерывных величин.
|
|
|
В механической интерпретации математическое ожидание непрерывной случайной величины сохраняет тот же смысл – абсцисса центра тяжести в случае, когда масса распределена по оси абсцисс непрерывно, с плотностью 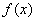. Эта интерпретация часто позволяет найти математическое ожидание без вычисления интеграла (5.6.2), из простых механических соображений.
Выше мы ввели обозначение 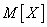для математического ожидания величины . В ряде случаев, когда величина 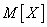входит в формулы как определенное число, её удобнее обозначать одной буквой. В этих случаях мы будем обозначать математическое ожидание величины через 
:
.
Обозначения и 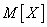для математического ожидания будут в дальнейшем применяться параллельно в зависимости от удобства той или иной записи формул. Условимся также в случае надобности сокращать слова «математическое ожидание» буквами м.о.
Следует заметить, что важнейшая характеристика положения – математическое ожидание – существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых математического ожидания не существует, так как соответствующая сумма или интеграл расходятся.
Рассмотрим, например, прерывную случайную величину с рядом распределения:
Нетрудно убедится в том, что , т.е. ряд распределения имеет смысл; однако сумма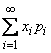 
в данном случае расходится и, следовательно, математического ожидания величины не существует. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно, обладают математическим ожиданием.
Выше мы дали формулы (5.6.1) и (5.6.2), выражающие математическое ожидание соответственно для прерывной инепрерывной случайной величины .
|
|
|
Если величина принадлежит к величинам смешанного типа, то её математическое ожидание выражается формулой вида:
, (5.6.3)
где сумма распространяется на все точки , в которых функция распределения терпит разрыв, а интеграл – на все участки, на которых функция распределения непрерывна.
Кроме важнейшей из характеристик положения – математического ожидания, - на практике иногда применяются и другие характеристики положения, в частности, мода и медиана случайной величины.
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Условимся обозначать моду буквой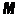 
. На рис. 5.6.1 и 5.6.2 показана мода соответственно для прерывной и непрерывной случайных величин.
Рис. 5.6.1
Рис. 5.6.2.
Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется «полимодальным» (рис. 5.6.3 и 5.6.4).
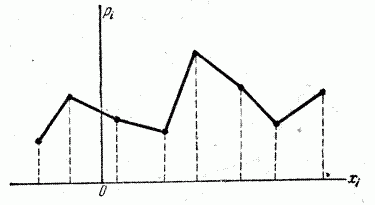
Рис. 5.6.3.
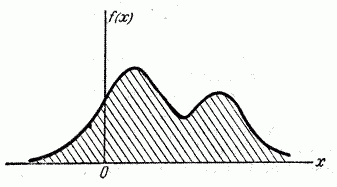
Рис. 5.6.4.
Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом (рис. 5.6.5 и 5.6.6). Такие распределения называют «антимодальными». Примером антимодального распределения может служить распределение, полученное в примере 5, n° 5.1.
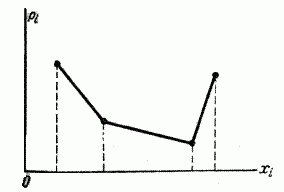
Рис. 5.6.5.
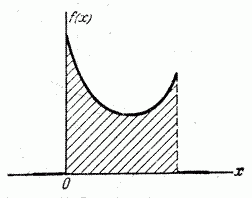
Рис. 5.6.6.
В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины.
Медианой случайной величины называется такое её значение 
, для которого
,
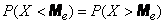т.е. одинаково вероятно, окажется ли случайная величина меньше или больше . Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 5.6.7).
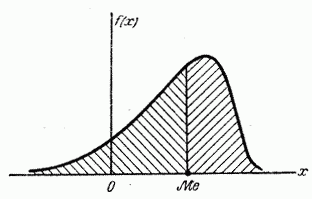
Рис. 5.6.7.
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
|
|
|
