 |
Производная от случайной функции
|
|
|
|
Дана случайная функция 
с математическим ожиданием 
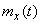и корреляционной функцией 
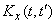. Случайная функция 
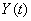связана со случайной функцией линейным однородным оператором дифференцирования:
. (15.7.14)
Требуется найти 
и 
.
Представим производную в виде предела:
. (15.7.15)
Применяя к равенству (15.7.15) операцию математического ожидания, получим:
.
Итак,
, (15.7.16)
т. е. математическое ожидание производной от случайной функции равно производной от ее математического ожидания. Следовательно, операцию дифференцирования, как и операцию интегрирования. тоже можно менять местами с операцией математического ожидания.
Для определения перейдем к центрированным случайным функциям 
и 
; очевидно:
. (15.7.17)
По определению
.
Подставим вместо и 
их выражения:
.
Представим выражение под знаком математического ожидания в виде второй смешанной частной производной:
. (15.7.18)
Мы доказали, что математическое ожидание производной случайной функции равно производной от математического ожидания, т. е. знаки дифференцирования и математического ожидания можно менять местами. Следовательно,
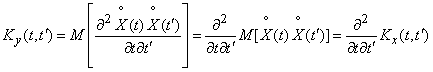. (15.7.19)
Таким образом,
. (15.7.20)
Итак, чтобы найти корреляционную функцию производной, нужно дважды продифференцировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем - по другому.
Сравнивая правила нахождения математического ожидания и корреляционной функции для двух рассмотренных нами линейных однородных операторов, мы видим, что они совершенно аналогичны, а именно: для нахождения математического ожидания преобразованной случайной функции тот же линейный оператор применяется кматематическому ожиданию исходной случайной функции; для нахождения корреляционной функции тот же линейный оператор применяется дважды к корреляционной функции исходной случайной функции. В первом частном случае это было двойное интегрирование, во втором - двойное дифференцирование.
|
|
|
Можно доказать, что такое правило является общим для всех линейных однородных операторов. Мы здесь сформулируем это общее правило без доказательства.
Если случайная функция с математическим ожиданием 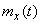и корреляционной функцией 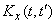преобразуется линейным однородным оператором 
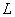в случайную функцию,
,
то для нахождения математического ожидания случайной функции 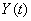нужно применить тот же оператор к математическому ожиданию случайной функции :
, (15.7.21)
а для нахождения корреляционной функции нужно дважды применить тот же оператор к корреляционной функциислучайной функции , сначала по одному аргументу, затем - по другому:
. (15.7.22)
В формуле (15.7.22) значки 
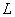у знака оператора указывают, по какому аргументу он применяется.
Во многих задачах практики нас, в конечном счете, интересует не корреляционная функция на выходелинейной системы, а дисперсия 
, характеризующая точность работы системы в условиях наличия случайных возмущений. Дисперсию можно найти, зная корреляционную функцию:
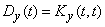. (15.7.23)
При этом нужно подчеркнуть, что, как правило, для определения дисперсии на выходе линейной системы недостаточно знать дисперсию на ее входе, а существенно важно знать корреляционную функцию. Действительно,линейная система может совершенно по-разному реагировать на случайные возмущения, поступающие на ее вход, в зависимости от того, какова внутренняя структура этих случайных возмущений; состоят ли они, например, по преимуществу из высокочастотных или низкочастотных колебаний. Внутренняя же структура случайного процессаописывается не его дисперсией, а корреляционной функцией.
Пример. На вход дифференцирующего механизма поступает случайная функция сматематическим ожиданием 
и корреляционной функцией
|
|
|
,
где 
- постоянная дисперсия случайной функции .
Определить математическое ожидание и дисперсию на выходе системы.
Решение. Случайная функция 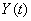на выходе системы (реакция) связана с воздействием оператором дифференцирования:
.
Применяя общие правила, имеем:
;
.
Полагая 
, имеем:
,
или, замечая, что не зависит от 
,
.
Итак, дисперсия на выходе дифференцирующего механизма зависит не только от дисперсии на входе, но также и от коэффициента 
, характеризующего быстроту затухания корреляционной связи между сечениями случайной функции при возрастании промежутка между ними. Если коэффициент мал, корреляционная связь затухает медленно, случайная функция изменяется со временем сравнительно плавно, и, естественно, дифференцирование такой функции приводит к сравнительно малым ошибкам. Напротив, если коэффициент велик,корреляционная функция убывает быстро; в составе случайной функции преобладают резкие, беспорядочные высокочастотные колебания; естественно, дифференцирование такой функции приводит к большим случайным ошибкам. В таких случаях обычно прибегают к сглаживанию дифференцируемой функции, т. е. так меняют оператор системы, чтобы он давал меньшие случайные ошибки на выходе.
|
|
|
