 |
Сложение случайных функций
|
|
|
|
Во многих задачах практики мы встречаемся с тем, что на вход динамической системы поступает не одна случайная функция 
, а две или более случайные функции, каждая из которых связана с действием отдельного возмущающего фактора. Возникает задача сложения случайных функций, точнее - задача определения характеристик суммы по характеристикам слагаемых.
Эта задача решается элементарно просто, если две складываемые случайные функции независимы (точнее, некоррелированны) между собой. В общем же случае для ее решения необходимо знание еще одной характеристики - так называемой взаимной корреляционной функции (иначе - корреляционной функции связи).
Взаимной корреляционной функцией двух случайных функций и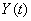 
называется неслучайная функция двух аргументов 
и 
, которая при каждой паре значений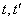 
равна корреляционному моменту соответствующих сечений случайной функции и случайной функции :
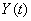. (15.8.1)
Взаимная корреляционная функция, так же как и обычная корреляционная функция, не изменяется при прибавлении к случайным функциям любых неслучайных слагаемых, а следовательно, и при центрированиислучайных функций.
Из определения взаимной корреляционной функции вытекает следующее ее свойство:
. (15.8.2)
Вместо функции 
часто пользуются нормированной взаимной корреляционной функцией:
. (15.8.3)
Если взаимная корреляционная функция равна нулю при всех значениях 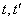, то случайные функции и 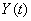называются некоррелированными (несвязанными).
На практике обычно суждение о некоррелированности случайных функций составляют не на основании равенства нулю взаимной корреляционной функции, а, наоборот, взаимную корреляционную функцию полагают равной нулю на основании физических соображений, свидетельствующих о независимости случайных функций.
|
|
|
Пусть, например, два самолета обстреливают наземную цель; обозначим , 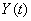углы пикирования первого и второго самолетов в процессе выполнения боевой операции. Если самолеты заходят на цель поодиночке, естественно считать случайные функции и 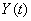некоррелированными; если же маневр выполняется самолетами совместно, причем один из них является ведущим, а другой - ведомым, очевидно наличие корреляционной связи между функциями и .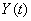
Вообще, если из физических соображений, связанных с существом решаемой задачи, вытекает наличие зависимости между фигурирующими в задаче случайными функциями, то их взаимные корреляционные функциидолжны быть обследованы.
Зная математические ожидания и корреляционные функции двух случайных функций и 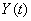, а также их взаимную корреляционную функцию, можно найти характеристики суммы этих двух случайных функций:
. (15.8.4)
По теореме сложения математических ожиданий:
, (15.8.5)
т. е. при сложении двух случайных функций их математические ожидания складываются.
Для определения корреляционной функции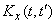 
перейдем к центрированным случайным функциям 
, 
, 
. Очевидно,
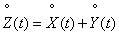. (15.8.6)
По определению корреляционной функции
,
или
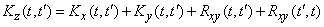. (15.8.7)
Формула (15.8.7) аналогична формуле (10.2.7) для дисперсии суммы случайных величин.
В случае, когда случайные функции и 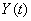некоррелированны, 
, и формула (15.8.7) принимает вид:
, (15.8.8)
т. е. при сложении некоррелированных случайных функций их корреляционные функции складываются.
Выведенные формулы могут быть обобщены на случай произвольного числа слагаемых. Если случайная функция есть сумма 
случайных функций:
, (15.8.9)
то ее математическое ожидание выражается формулой
, (15.8.10)
а ее корреляционная функция - формулой
, (15.8.11)
где суммирование распространяется на все возможные размещения индексов 
и 
попарно.
|
|
|
В случае, когда все случайные функции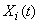 
некоррелированны, формула (15.8.11) превращается в теорему сложения корреляционных функций:
, (15.8.12)
т. е. корреляционная функция суммы взаимно некоррелированных случайных функций равна суммекорреляционных функций слагаемых.
Формула (15.8.12) аналогична теореме сложения дисперсий для обычных случайных величин.
Частным случаем сложения случайных функций является сложение случайной функции со случайной величиной.
Рассмотрим случайную функцию с характеристиками 
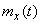и и 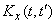случайную величину 
с математическим ожиданием 
и дисперсией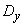 
. Предположим, что случайная функция ислучайная величина некоррелированны, т. е. при любом
.
Сложим случайную функцию со случайной величиной ; получим случайную функцию
. (15.8.13)
Определим ее характеристики. Очевидно,
. (15.8.14)
Чтобы найти 
, пользуясь теоремой сложения корреляционных функций (15.8.8), рассмотримслучайную величину как частный случай случайной функции, не меняющейся во времени, и найдем ее корреляционную функцию:
. (15.8.15)
Применяя формулу (15.8.8), получим:
,
т. е. при прибавлении к случайной функции некоррелированной с нею случайной величины ккорреляционной функции прибавляется постоянное слагаемое, равное дисперсии этой случайной величины.
|
|
|
