Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций

В предыдущем мы познакомились с методом непосредственного определения характеристик случайной функции из опыта. Такой метод применяется далеко не всегда. Во-первых, постановка специальных опытов, предназначенных для исследования интересующих нас случайных функций, может оказаться весьма сложной и дорогостоящей. Во-вторых, часто нам требуется исследовать случайные функции, характеризующие ошибки приборов, прицельных приспособлений, систем управления и т. д., еще не существующих, а только проектируемых или разрабатываемых. При этом обычно исследование этих ошибок и предпринимается именно для того, чтобы рационально выбрать конструктивные параметры системы так, чтобы они приводили к минимальным ошибкам. Ясно, что при этом непосредственное исследование случайных функций, характеризующих работу системы, нецелесообразно, а в ряде случаев вообще невозможно. В таких случаях в качестве основных рабочих методов применяются не прямые, а косвенные методы исследования случайных функций. Подобными косвенными методами мы уже пользовались при исследовании случайных величин: ряд глав нашего курса - гл. 10, 11, 12 - был посвящен нахождению законов распределения и числовых характеристик случайных величин косвенно, по законам распределения и числовым характеристикам других случайных величии, с ними связанных. Пользуясь совершенно аналогичными методами, можно определять характеристики случайных функций косвенно, по характеристикам других случайных функций, с ними связанных. Развитие таких косвенных методов и составляет главное содержание прикладной теории случайных функций.

Задача косвенного исследования случайных функций на практике обычно возникает в следующей форме.

Имеется некоторая динамическая система ; под «динамической системой» мы понимаем любой прибор, прицел, счетно-решающий механизм, систему автоматического управления и т. п. Эта система может быть механической, электрической или содержать любые другие элементы. Работу системы будем представлять себе следующим образом: на вход системы непрерывно поступают какие-то входные данные; система перерабатывает их и непрерывно выдает некоторый результат. Условимся называть поступающие на вход системы данные: «воздействием», а выдаваемый результат «реакцией» системы на это воздействие. В качестве воздействий могут фигурировать изменяющиеся напряжения, угловые и линейные координаты каких-либо объектов, сигналы или команды, подаваемые на систему управления, и т. п. Равным образом и реакция системы может вырабатываться в той или иной форме: в виде напряжений, угловых перемещений и т. д. Например, для прицела воздушной стрельбы воздействием является угловая координата движущейся цели, непрерывно измеряемая в процессе слежения, реакцией - угол упреждения.

Рассмотрим самый простой случай: когда на вход системы подается только одно воздействие, представляющее собой функцию времени : реакция системы на это воздействие есть другая функция времени . Схема работы системы условно изображена на рис. 15.5.1.

Рис. 15.5.1.

Будем говорить, что система осуществляет над входным воздействием некоторое преобразование, в результате которого функция преобразуется в другую функцию . Запишем это преобразование символически в виде:

. (15.5.1)

Преобразование может быть любого вида и любой сложности. В наиболее простых случаях это, например, умножение на заданный множитель (усилители, множительные механизмы), дифференцирование или интегрирование (дифференцирующие или интегрирующие устройства). Однако на практике системы, осуществляющие в чистом виде такие простейшие преобразования, почти не встречаются; как правило, работа системы описывается дифференциальными уравнениями, и преобразование сводится к решению дифференциального уравнения, связывающего воздействие с реакцией .

При исследовании динамической системы в первую очередь решается основная задача: по заданному воздействию определить реакцию системы . Однако для полного исследования системы и оценки ее технических качеств такой элементарный подход является недостаточным. В действительности воздействие никогда не поступает на вход системы в чистом виде: оно всегда искажено некоторыми случайными ошибками (возмущениями), в результате которых на систему фактически воздействует не заданная функция , аслучайная функция ; соответственно этому система вырабатывает в качестве реакции случайную функцию 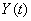, также отличающуюся от теоретической реакции (рис. 15.5.2).

Рис. 15.5.2.

Естественно возникает вопрос: насколько велики будут случайные искажения реакции системы при наличии случайных возмущений на ее входе? И далее: как следует выбрать параметры системы для того, чтобы эти искажения были минимальными?

Решение подобных задач не может быть получено методами классической теории вероятностей; единственным подходящим математическим аппаратом для этой цели является аппарат теории случайных функций.

Из двух поставленных выше задач, естественно, более простой является первая - прямая - задача. Сформулируем ее следующим образом.

На вход динамической системы поступает случайная функция ; система подвергает ее известному преобразованию, в результате чего на выходе системы появляется, случайная функция:

. (15.5.2)

Известны характеристики случайной функции : математическое ожидание и корреляционная функция. Требуется найти аналогичные характеристики случайной функции 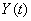. Короче: по заданным характеристикам случайной функции на входе динамической системы найти характеристики случайной функции на выходе.

Поставленная задача может быть решена совершенно точно в одном частном, но весьма важном для практики случае: когда преобразование принадлежит к классу так называемых линейных преобразований и соответственно система принадлежит к классу линейных систем.

Содержание этих понятий будет пояснено в следующем .