Измерение степени тесноты корреляционной связи в случае парной зависимости

Следующей задачей корреляционного метода анализа является измерение тесноты связи, то есть степени влияния факторного признака на вариацию результативного признака.

Первые попытки установления тесноты взаимосвязи сделал Г. Фехнер, предложивший простейший показатель коэффициент корреляции знаков. Он основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков.

,

где: – коэффициент корреляции знаков;

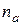– число совпадений знаков отклонений индивидуальных величин от средней;

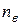– число несовпадений знаков отклонений индивидуальных

величин от средней.

Показатель Фехнера изменяется от –1 до +1: при =1 имеет место полная прямая связь, при =0 – связь отсутствует, = –1 показывает полную обратную связь.

Рассчитаем коэффициент корреляции Фехнера на основе табл. 9.1.

Таблица 9.1

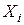
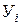
Насе-ленные пункты	Число подростков, которые не учатся и не работают на 1000 несовершеннолетних	Уровень преступности несовершен-нолетних на 1000 несовершеннолетних	Знаки отклонений индивидуальных значений признака от средней	Совпадение (а) или несовпадение (в) знаков
для	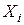для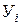
			-	-	а
			-	-	а
		4,5	-	-	а
			-	-	а
			-	+	в
		6,3	+	+	а
		5,3	+	-	в
		6,4	+	+	а
		7,8	+	+	а
		6,6	+	+	а
		10,3	+	+	а
Итого		68,2

 

Среднее число подростков, которые не учатся и не работают на 1 000 несовершеннолетних составит:

Средний уровень преступности несовершеннолетних на 1 000 несовершеннолетних составит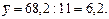

В графах 4 и 5 табл. 9.1 указаны знаки отклонений значений признаков от соответствующей средней.

Подсчитав число совпадений знаков 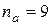и число несовпадений знаков (см гр 6 табл. 9.1) рассчитаем коэффициент Фехнера:

 

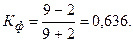
Полученная величина показателя Фехнера свидетельствует о прямой связи между сопоставляемыми признаками.

Недостаток данного показателя заключается в том, что при определении размера коэффициента разные по абсолютной величине отклонения имеют равный вес. На основе коэффициента Фехнера поэтому нельзя судить о степени тесноты и оценке существенности корреляционной связи. При малом объеме информации он отвечает на вопрос о наличии и направлении связи между признаками.

В качестве более совершенного измерителя связи между признаками используется линейный коэффициент корреляции. При расчете этого показателя можно использовать следующую формулу:

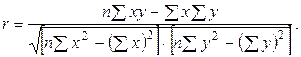
Линейный коэффициент корреляции может принимать значения в пределах 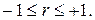При 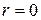корреляция отсутствует, а если 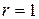– связь функциональная.

По степени тесноты связи различают следующие количественные критерии оценки тесноты связи (табл. 9.2).

Таблица 9.2

 

Коэффициент корреляции	Характер связи
до 0,3	Практически отсутствует
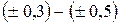
	Слабая
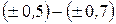
	Умеренная
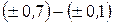
	Сильная

 

Используя данные табл. 9.2 рассчитаем линейный коэффициент корреляции.

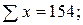
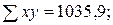
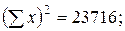
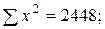
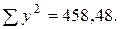
=0,7949.

Полученная величина линейного коэффициента корреляции свидетельствует о возможном наличии достаточно тесной прямой зависимости между рассматриваемыми признаками.

Квадрат коэффициента корреляции 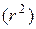носит название коэффициента детерминации. Для нашего примера его величина составляет 0,6319, а это означает, что 63,19% вариации уровня преступности несовершеннолетних объясняется подростковой безнадзорностью.

Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае наличия линейной зависимости между признаками.

В случаях криволинейной зависимости между явлениями линейный коэффициент корреляции теряет смысл и для измерения тесноты связи применяют так называемое эмпирическое корреляционное отношение 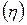, предложенное К. Пирсоном. Расчет корреляционного отношения основан на использовании теоремы сложения дисперсий. Общая дисперсия результативного признака является суммой двух дисперсий: межгрупповой и средней из внутригрупповых дисперсий.

Межгрупповая дисперсия отражает колеблемость результативного признака под воздействием учтенного признака – фактора, положенного в основу группировки.

,

где 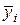- средние значения результативного признака в каждой группе;

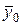– общая средняя результативного признака для всей совокупности;

f – число единиц в каждой группе.

Средняя из внутригрупповых дисперсий 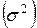показывает колеблемость результативного признака под влиянием всех других неучтенных факторов (остаточная дисперсия).

,

 

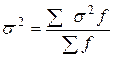где 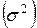– дисперсия результативного в соответствующей группе.

Общая дисперсия равна .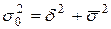

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: