 |
Система индексов средних качественных показателей
|
|
|
|
Динамика среднего качественного показателя (средней цены, средней себестоимости, средней заработной платы и т.д.), находится под влиянием двух факторов: изменения качественных показателей (признаков) у каждой единицы совокупности и структурных сдвигов в составе совокупности. Например, изменение средней заработной платы водителей автотранспортного предприятия зависит от динамики заработной платы водителей каждого класса и от структурных сдвигов в составе водителей. Рост удельного веса водителей I класса, у которых уровень зарплаты выше, ведет к росту средней зарплаты на предприятии.
Динамику среднего качественного показателя и факторы этой динамики статистика изучает с помощью системы трех индексов: индекса переменного состава, постоянного (фиксированного) состава и индекса влияния структурных сдвигов.
Индекс переменного состава – это показатель динамики средней величины, он находится под влиянием двух названных факторов одновременно.
Индекс постоянного состава характеризует изменение среднего качественного показателя вследствие влияния только первого фактора – динамики качественного показателя у каждой единицы совокупности.
Индекс влияния структурных сдвигов показывает изменение среднего качественного показателя в результате структурных сдвигов в составе изучаемой совокупности.
Заметим, что при построении этих индексов применяется то же правило выбора периода весов, что и в агрегатных индексах.
Абсолютное изменение определяется как разность средних уровней качественных показателей.
Эти индексы взаимосвязаны:

Пусть имеются данные о себестоимости (С) и выпуске изделия "А" по двум предприятиям акционерного общества, которые приведены в табл. 10.5.
|
|
|
Таблица 10.5
| Предприятия | Себестоимость изделия "А", тыс. р. | Выпуск, тыс. шт. | Структура выпуска, % | |||
| базисный период | отчетный период | базисный период | отчетный период | базисный период | отчетный период | |
| 24,5 | ||||||
| Итого | - | - |
Индекс средней себестоимости переменного состава:

Средняя себестоимость единицы продукции изделия "А" по акционерному обществу снизилась на 7,3% (92,7-100) или на 1,64 тыс. р.
Изменение средней себестоимости было обусловлено влиянием двух факторов.
1. Динамикой себестоимости единицы продукции на каждом предприятии, а именно снижением себестоимости на предприятии 1 с 20 до 18 тыс. р., на предприятии 2 с 25 до 24,5 тыс. р.
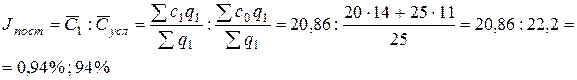
Следовательно, влияние данного фактора привело к снижению себестоимости единицы продукции на 6% (94-100) или на 1,34 тыс. р.
2. Структурными сдвигами в составе выпуска продукции

Структурные сдвиги в составе выпуска продукции привели к снижению средней себестоимости по акционерному обществу на 1,3% (98,7-100) или на 0,3 тыс. р.
Структурные сдвиги в выпуске продукции выразились в изменении удельного веса выпуска продукции каждого предприятия. Возросла доля выпуска продукции предприятия № 1 с 50 до 56%, где более низкий уровень себестоимости, что и привело к снижению средней себестоимости по АО.
Проверим правильность расчетов на основе взаимосвязи индексов и абсолютных приростов.
 .
.
 .
.
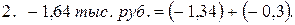
Систему этих индексов можно вычислить и по формулам с использованием показателей доли выпуска продукции по предприятиям.



Цепные и базисные индексы
Индексы, как и относительные величины динамики, могут быть цепными и базисными. Индивидуальные базисные и цепные индексы, тождественные базисным и цепным коэффициентам роста и существующим между ними взаимосвязям изложены в теме «Ряды динамики».
|
|
|
Цепные и базисные индексы можно вычислить и для общих агрегатных индексов. При этом индексы количественных показателей строятся на основе применения постоянных базисных весов.
| Периоды времени | I | II | III |
| Цепные индексы | 
| 
| 
|
| Базисные индексы | 
| 
| 
|
Очевидно, что для этих индексов применима та же взаимосвязь, которая существует для индивидуальных индексов:
1) произведение цепных индексов равно последнему базисному индексу;
|
|
|


