 |
Определение тесноты связи между атрибутивными признаками
|
|
|
|
При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака составляется таблица «четырех полей», частоты которой обозначаются соответственно а, в, с, d.
Рассмотрим связь между полом преступников и местом их проживания.
Таблица 9.6
| Пол | Число лиц, совершивших преступление | ||
| городское | сельское | всего | |
| Мужчины | 240 (а) | 130 (в) | 370 (а+в) |
| Женщины | 42 (с) | 18 (d) | 60 (с+d) |
| Всего | 282 (а+с) | 148 (в+d) |
Для установления наличия связи между признаками, вычислим удельные веса по результативному признаку: доля преступников, проживающих в городе среди мужчин составляет 64,9% (240:370)х100, а среди женщин 70% (42:60)х100%. Результаты расчетов подтверждают наличие связи.
Степень тесноты связи между признаками можно оценить с помощью коэффициентов контингенции или ассоциации.
Коэффициент контингенции вычисляется по формуле:
.
Подставив в формулу значения частот, получим:
Величина коэффициента говорит о наличии слабой обратной связи между анализируемыми признаками.
Коэффициент ассоциации равен:
,
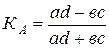Коэффициент ассоциации подтверждает наличие слабой обратной связи между полом и местом проживания преступников.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Сравнение этих коэффициентов исчисленных по одной и той же исходной информации, свидетельствует о том, что коэффициент контингенции дает более осторожную оценку степени тесноты связи.
В тех случаях, когда хотя бы один из четырех показателей в таблице «четырех полей» отсутствует, величина коэффициента ассоциации будет равна единице, что дает преувеличенную оценку степени тесноты связи между признаками и предпочтение следует отдать коэффициенту контингенции.
|
|
|
Коэффициенты ассоциации и контингенции могут принимать любые значения от –1 до 1. Когда коэффициент равен 0, связи между данными явлениями нет совершенно, когда равен 
-между явлениями существует функциональная связь. Словом величина коэффициента как показателя связи истолковывается так же, как и величина коэффициента корреляции.
Множественная корреляция
Все ранее изложенные показатели корреляции относились к измерению связи между двумя признаками. На практике же чаще всего приходится иметь дело со многими факторами, влияющими на изменение изучаемого показателя. В силу этого при статистическом исследовании сталкиваются с необходимостью заниматься в меньшей степени парной корреляцией, а в большей – множественной, т. е. такой по средством которой изучается зависимость результативного признака от ряда признаков - факторов.
Принципиальная сложность множественной корреляции – это отбор факторов на основе качественного анализа всей системы признаков, влияющих на изменение изучаемого показателя, например, уровня преступности. Из всей системы признаков исключаются, во первых, такие признаки, которые уже по многим соображениям малозначительны во вторых, такие, которые невозможно количественно измерить в силу отсутствия информации.
Затем выясняют насколько существенны отобранные признаки – факторы. В частности вычисляются парные и частные коэффициенты корреляции, коэффициенты эластичности.
Отобрав соответствующие значимые факторы, устанавливают конкретный вид уравнения связи, рассчитывают величину совокупного коэффициента корреляции.
Коэффициент множественной корреляции измеряет степень тесноты связи между результативным признаком и совокупностью факторных признаков. Применительно к влиянию на у двух факторов (х, z) этот коэффициент будет следующим:
|
|
|
,
где 
, 
, 
.
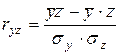Коэффициент множественной корреляции является всегда положительным числом. Он может принимать любое значение в пределах между 0 и 1. Чем ближе он к единице, тем теснее зависимость у от совокупного действия х и z.
При изучении зависимости явлений часто приобретает особое значение необходимость устранения влияния одного какого – либо фактора, чтобы можно было лучше выявить влияние другого фактора. Для этого применяется построение частных коэффициентов корреляции. Исчисляются эти показатели на основе парных коэффициентов корреляции.
Для случая зависимости у от двух признаков можно вычислить два коэффициента частной корреляции (r);
,
.
В первой формуле определяется степень тесноты связи между у и х при изоляции влияния фактора z. Во второй формуле определяется степень тесноты связи z и у при изоляции влияния фактора х.
Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака:
.
Коэффициенты частной корреляции могут принимать отрицательные значения и колебаться как и обычный линейный коэффициент корреляции в пределах от –1 до +1.
Множественная корреляция изучается и другими методами. В частности на основе построения многофакторных регрессионных моделей, которые используются как для сравнительного анализа, так и в прогнозировании.
Всегда следует проверять на сколько существенны коэффициенты множественной и парной корреляции, а также возможности экстраполяции при применении регрессионных моделей.
В целом методология множественной корреляции основывается на общих принципах парной корреляции. Однако в ней многие проблемы усложняются, значительно возрастает и сложность математического аппарата анализа. Сегодня широкое распространение получили пакеты прикладных программ по статистике для персональных компьютеров, ликвидировавшие трудоемкость расчетов. Однако сохранилось значение исследователя при формировании информационного массива и содержательной интерпретации полученных результатов.
Тема 10. Индексы
|
|
|
