Учебно-методическое обеспечение самостоятельной работы студентов

Самостоятельная работа студентов реализуется в разных видах. Она включает подготовку студентов к семинарским (практическим) занятиям. Для этого студент изучает лекции преподавателя, основную, дополнительную литературу, Интернет-ресурсы, рекомендованные в разделе8 «Учебно-методическое и информационное обеспечение дисциплины». Самостоятельная работа предусматривает также решение во внеучебное время практических заданий, приведённых в разделе 7 «Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины».К самостоятельной работе студента относится подготовка к зачёту. Вопросы к зачёту приведены также в разделе 7. Обязательным является решение студентом в течение семестра домашней расчётной работы.

При реализации игровой практики на занятиях в Академии применяется игровой сервер, расположенный в сети Интернет.

Для входа требуется зайти на Сетевое окружение, выбрать каталог Student на Nyx.

(В случае проблем с поиском этого каталога можно зайти другим путем: В меню Пуск выбрать Выполнить, в появившемся окне написать путь \\nyx, в каталоге Nyx выбрать каталог Student).

Далее, выбрать каталог Теория игр, в нем каталог GamblerJ, далее bin, и файл Gambler. При этом должно появиться окно Гамблер, в котором следует прописать настройки соединения и зарегистрироваться.

В настройках соединения следует поставить галочку около текста «использовать прокси», прописать сервер proxy.tiiel.ru, порт 8080.

В настройках соединения следует поставить галочку около текста «прокси-сервер требует авторизации», прописать свои логин и пароль из нашей сети (которые используются для выхода в домен College).

После загрузки Гамблера система предложит вам зарегистрироваться на нём. Для этого надо выбрать себе ник(логин) и пароль. При желании можно написать там несколько слов про себя и загрузить свой аватар.

Вообще говоря, играть в бридж через Интернет, можно и дома. Только для этого потребуется выйти на сайт www.gambler.ru и скачать клиентскую базу. Можно зайти с тем же самым ником или создать новый.

 

Методические указания и задания для выполнения контрольной работы

Студентами заочной формы обучения

Контрольная работа предназначена для студентов заочной формы обучения и позволяет увеличить объем знаний путем самостоятельного изучения дополнительного материала и проверки уже полученных знаний. В ходе подготовки к контрольной работе рекомендуется использовать данный УМК по дисциплине. Контрольная работа выполняется студентом в межсессионный период и защищается у руководителя. Студенты, не выполнившие контрольную работу, не допускаются к сдаче зачета. Работа должна быть оформлена на листах формата А4, 14 шрифтом. Титульный лист контрольной работы должен быть оформлен в соответствии с установленными требованиями для подготовки контрольных работ.

Контрольная работа выполняется по одному из вариантов, номер которого устанавливается в соответствии с последними двумя цифрами номера зачетной книжки путем вычисления остатка от деления на 20 или посредством следующей таблицы.

 

две последние цифры номера зачетки	№ варианта	две последние цифры номера зачетки	№ варианта
01, 21, 41, 61, 81		11, 31, 51, 71, 91
02, 22, 42, 62, 82		12, 32, 52,72, 92
03, 23, 43, 63, 83		13, 33, 53, 73, 93
04, 24, 44, 64, 84		14, 34, 54, 74, 94
05, 25, 45, 65, 85		15, 35, 55, 75, 95
06, 26, 46, 66, 86		16, 36, 56, 76, 96
07, 27, 47, 67, 87		17, 37, 57, 77, 97
08, 28, 48, 68, 88		18, 38, 58, 78, 98
09, 29, 49, 69, 89		19, 39, 59, 79, 99
10, 30, 50,70, 90		20, 40, 60, 80, 100

 

В соответствии с номером варианта студенты выбирают и решают задачи, приведенные в темах 3 (две задачи), 4, 6, 8, 12.

 

Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины

ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Раздел 1. Введение в теорию игр

Тема 1. Общее введение в теорию игр

Контрольные вопросы

1. Столкновение интересов.

2. Исторический обзор.

3. Основные понятия теории игр.

4. Классификация игр.

5. Формальные представления игр.

6. Позиционные игры.

7. Игры с бесконечным множеством чистых стратегий.

8. Игры, не имеющие цены.

9. Игры, связанные с выбором времени или распределением средств.

10. Стохастические игры.

11. Рекурсивные игры.

12. Игры на выживание.

13. Игры на истощение.

14. Теория игр и социология.

15. Дерево игры.

16. Информационные множества.

17. Исходы. разумность и знание.

18. Чистые и смешанные стратегии.

18. Литература основная: [1–4]; дополнительная: [5-18].

18.

Тема 2. Теория полезности

Контрольные вопросы

 

1. Классы выборов решения.

2. Индивидуальный выбор решения при определенности.

3. Примеры: линейное программирование.

4. Индивидуальный выбор решения при риске.

5. Портфель инвестиций.

6. Аксиоматическая трактовка полезности.

7. Некоторые распространенные заблуждения.

8. Сравнение индивидуальных полезностей.

9. Экспериментальное определение полезности.

9. Литература основная: [1–4]; дополнительная: [6, 12, 14, 16].

9.

 

Раздел 2. Игры двух лиц

Тема 3. Игры 2 лиц с нулевой суммой

Контрольные вопросы

1. Матричные игры.

2. Игры со строгим соперничеством и с нестрогим соперничеством.

3. Игры с уравновешенными парами.

4. Игры без уравновешенных пар.

5. Принципы решения матричных антагонистических игр.

6. Принцип минимакса.

7. Оптимальное поведение игроков.

8. Свойства оптимальных стратегий и цена игры.

9. Игры 2х2.

10. Доминирование.

11. Игры 2хn, mх2.

12. Графическое решение.

13. Решение игр mхn симплекс-методом.

14. Итеративный метод Брауна.

15. Применение теории игр для анализа проблем микроэкономики.

15. Литература основная: [1–4]; дополнительная: [5-10, 17].

15.

Типовые примеры

Решение игр 2х2.

Рассмотрим матричную игру с матрицей ,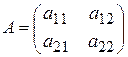

не имеющей седловой точки.

Антагонистическая игра, в которой каждый игрок имеет конечное число стратегий, называется матричной игрой. Если игрок 1 имеет m стратегий, а игрок 2 имеет n стратегий, то матричная игра может быть задана матрицей , где есть выигрыш игрока 1, если он выбирает стратегию i, а игрок 2 — стратегию j. Матрица A называется матрицей игры или матрицей выигрышей. Стратегии игроков, на основе которых сформирована матрица A, называются чистыми стратегиями. Игра, задаваемая матрицей с m строками и n столбцами, называется игрой mхn.

Оптимальный выбор игроками своих стратегий в матричной игре осуществляется на основе принципа минимакса: стремление игроков к максимизации своих выигрышей понимается как стремление получить наибольший гарантированный, т.е., не зависящий от выбора стратегий другим игроком, выигрыш. Следуя этому принципу, игрок 1 может гарантировать себе выигрыш не менее , а игрок 2 гарантировать себе проигрыш не более величины 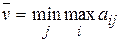. Величина 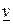(нижняя граница выигрыша игрока 1) называется нижней ценой игры, (верхняя граница проигрыша игрока 2) — верхней ценой игры. Стратегия 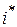игрока 1, обеспечивающая ему выигрыш не менее 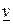, называется максиминной стратегией. Аналогично, стратегия игрока 2, обеспечивающая ему проигрыш не более , называется минимаксной стратегией. Для краткости максиминную и минимаксную стратегии принято называть просто минимаксными стратегиями.

Теорема. Равенство 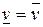имеет место тогда и только тогда, когда матрица A имеет седловую точку, т.е. элемент , для которого выполняется двойное неравенство

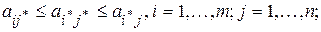(1)

при этом

. (2)

Число v называется ценой игры, минимаксные стратегии 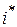, 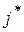называются оптимальными чистыми стратегиями соответственно игроков 1 и 2. Тройка 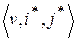называется также решением игры.

Ситуация 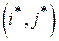в игре с седловой точкой является ситуацией равновесия: любое одностороннее отклонение каждым игроком от своей оптимальной стратегии может быть для него лишь невыгодно.

Следовательно, если в матрице есть седловая точка, решение находится среди чистых стратегий, иначе - среди смешанных стратегий. Произвольную смешанную стратегию x первого игрока представим в ви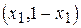де , где 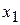— вероятность выбора им своей первой чистой стратегии, . Аналогично, произвольная смешанная стратегия второго игрока имеет вид , 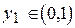. Задача имеет решение:

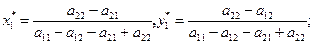
цена игры при этом равна

.

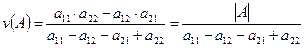Решение игр 2хn, mх2.

Рассмотрим сначала игру 2´ n с платежной матрицей

.

Будем предполагать, что седловой точки матрица A не имеет. Произвольную смешанную стратегию игрока 1 представим в виде , где 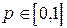. Если игрок 1 применяет смешанную стратегию x, а игрок 2 — свою j–ю чистую стратегию, то выигрыш игрока 1, очевидно, равен 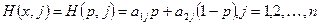, то есть линейно зависит от p.

По теореме

.

Исходя из этого соотношения, с помощью простых геометрических построений легко найти решение игры:

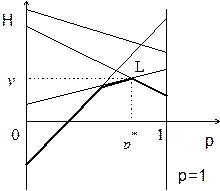Рис. 1.

- строим графики функций 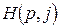для 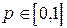. Получим n прямых (см. рис. 1). Эти прямые удобно строить по двум точкам — и 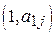. Первая из них находится на оси ординат H, вторая — на оси ;

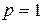- строим график функции

—

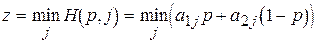нижнюю огибающую всех прямых, соответствующих стратегиям игрока 2. Значения этой функции, соответствуют выигрышу игрока 1, когда он применяет стратегию 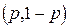, а противник действует наихудшим для него образом. На рис. 1 нижняя огибающая выделена жирной линией;

- наивысшая точка нижней огибающей (точка L на рис. 1) соответствует тому значению p, при котором достигается

.

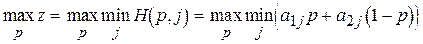Поэтому ордината точки L является значением игры, а ее абсцисса — первой компонентой оптимальной смешанной стратегии игрока 1: 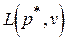.Если же таких высших точек будет более одной, т.е. огибающая будет иметь наивысший огибающий участок, то у игрока 1 существует бесконечное множество оптимальных смешанных стратегий, первые компоненты которых соответствуют абсциссам точек этого горизонтального участка.

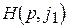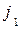Описанное построение позволяет исходную игру 2´ n свести к игре 2´2. Так как матрица игры не имеет седловой точки, то и в точке L пересекается не менее двух прямых с противоположным наклоном. Пусть и такие прямые. Интуитивно ясно, что игрок 2, пользуясь только двумя стратегиями и 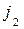, может не дать игроку 1 выиграть больше, чем v. Таким образом, оптимальное поведение в игре 2´2:

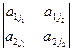
является оптимальным и в исходной игре 2´ n. Решение игры легко получить по формулам для игр 2х2.

В случае, когда нижняя огибающая имеет верхний горизонтальный участок, соответствующий чистой стратегии 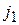, то 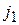будет единственной чистой оптимальной стратегией игрока 2.

Пусть теперь две чистые стратегии имеет игрок 2, а игрок 1 — произвольное их число. Матрица такой игры имеет вид:

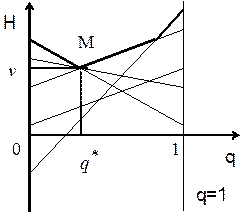Рис. 2.

.

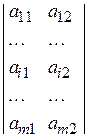Анализ этой игры выполняется аналогично предыдущему случаю. Отличие состоит лишь в том, что теперь, чтобы учесть интересы игрока 2, нужно исходить из соотношения (теорема):

,

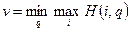где q — первая компонента смешанной стратегии игрока 2, а .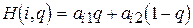

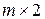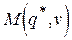Для перехода от исходной игры к игре используется точка — нижняя точка верхней огибающей семейства прямых 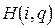(рис. 2).

Пример. Рассматривается задача разработки оптимального плана энергетического строительства в некотором регионе. Предположим, что имеются возможности строительства электростанций четырех типов: 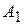, , 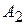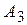и 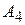(тепловые, гидравлические и т.д.). Эффективность каждого из четырех типов объектов зависит от разнородных факторов (наводнения, засуха, морозы), а также от цены топлива, расходов на его транспортирование и т. п. Допустим, что можно выделить (по крайней мере, ориентировочно) пять различных случаев, каждый из которых обозначает определенное сочетание факторов, влияющих на возможную эффективность энергетических объектов. Назовем их состояниями природы и обозначим через , , 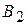, и .

Экономическая эффективность отдельных типов электростанций изменяется в зависимости от состояния природы в соответствии со следующей таблицей:

 

 

		Состояния природы
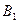
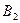
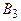
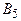
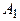
Типы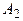
электростанций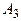

 

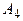
Будем рассматривать описанную ситуацию как игровую. Первый игрок (планирующие органы) располагает четырьмя стратегиями (по числу типов электростанций). Второй игрок («природа») действует случайно, но так, что к явлениям природы невозможно применить положения теории вероятностей. У него пять стратегий. В этих условиях табл. является, по существу, игровой матрицей. Ее анализ показывает, что у игрока 1 стратегии 1 и 2 доминируются стратегией 3 и поэтому могут быть исключены из рассмотрения. Приходим к игре с матрицей:

 

Теперь замечаем, что у игрока 2 стратегия 3 доминируется стратегией 2, а стратегия 2 — стратегией 4. Следовательно, имеет смысл анализировать игру 2´3, задаваемую матрицей:

 

Пусть 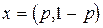— произвольная смешанная стратегия игрока 1 в этой игре. Найдем функции , :

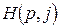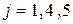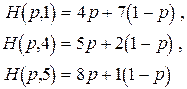
и построим их графики (рис. 3)

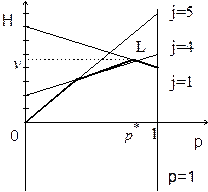Рис. 3.

Экстремальная точка L на нижней огибающей (отмечена жирной линией) является пересечением прямых, соответствующих 1–ой и 4–ой стратегиям игрока 2, поэтому рассматриваем игру 2´2:

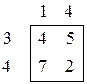
По формулам находим:

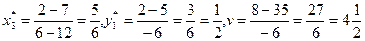Из полученных результатов формируем решение исходной игры:

.

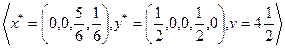Таким образом, для обеспечения региона электроэнергией целесообразно ограничиться строительством электростанций типов 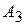и 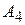в пропорции 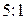. При этом экономическая эффективность такого решения никогда не будет ниже 4.5; если же учесть, что второй игрок — природа — скорее всего не будет применять своей оптимальной стратегии, то можно рассчитывать на более высокий показатель эффективности.

 

Задачи для решения

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: