 |
Тема 9. Индивидуальный выбор решения при неопределенности
|
|
|
|
Контрольные вопросы
1. Критерии выбора решения.
2. Аксиомы, не основанные на полном незнании. Аксиомы, основанные на полном незнании.
3. Случай частичного незнания.
4. Игры как выбор решения при неопределенности.
5. Выбор статистического решения при фиксированном эксперименте.
6. Выбор статистического решения при нефиксированном эксперименте.
7. Полные классы правильных решений.
7. Литература основная: [1–4]; дополнительная: [5, 6, 9-11, 13, 14, 16, 17].
Тема 10. Групповой выбор решения
Контрольные вопросы
1. Общий выбор и индивидуальные ценности.
2. Условия, накладываемые на групповой выбор и теорема Эрроу о невозможности.
3. Разбор парадокса Эрроу.
4. Процедура выбора группового решения, основанная на степенях индивидуальных предпочтений.
5. Правило большинства и его стратегическое использование.
6. Игры с целью справедливого дележа.
7. Политика в области дивидендов и игра на экономическое разорение.
7. Литература основная: [4]; дополнительная: [5, 6, 11, 16].
Тема 11.Случайные ходы и лотереи
Контрольные вопросы
1. Случайные ходы.
2. Моделирование.
3. Лотереи.
4. Ожидаемая полезность лотерей.
Литература основная: [1-4]; дополнительная: [5, 6, 11, 16, 17].
Тема 12. Равновесия Нэша
Контрольные вопросы
1. Равновесия Нэша.
2. Равновесия Нэша в смешанных стратегиях.
3. Рафинирование равновесий для развернутой формы.
3. Литература основная: [4]; дополнительная: [5, 6, 11, 15-17].
3.
Типовые примеры
Продолжим рассмотрение игры Семейный спор. В случае если игроки могут договариваться о совместных действиях, возникают новые ситуации в игре. Напомним матрицу игры.
| Муж/Жена | Балет | Футбол |
| Балет | (2,5) | (0,0) |
| Футбол | (3,3) | (5,2) |
Изобразим эту информацию на графике, откладывая выигрыши мужа по оси Ox, выигрыши жены – по оси Oy.
|
|
|
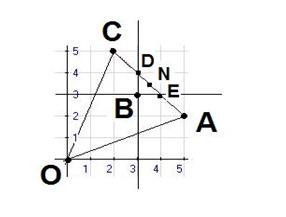
Точки O, A, B, C соответствуют чистым стратегиям. Отрезки, их соединяющие – смешанным стратегиям. Например, отрезок OA возникает при чередования с различными вероятностями стратегий, приводящих к исходам (0,0) и (5,2), т.е. если жена все время ходит на футбол, а муж – то на футбол, то на балет. Уже обсуждалось ранее, что для чистых стратегий точка B(3,3) – точкам равновесия. Также она возникает и из соображений доминирования. То есть эту точку каждый может себе гарантировать, не вступая в переговоры с партнером. Линии BE и BD показывают, чего может достичь игрок, не вступая в переговоры. Теперь обратим внимание на линию AC, расположенную справа-сверху, или, как говорят, северо-восточную границу области. Точки этой линии составляют так называемое Парето-оптимальное множество. Во-первых, они доминируют все остальные точки области, во-вторых, между собой они несравнимы. Напомним, что точка X(x1,x2) доминирует (лучше) точку (точки) Y(y1,y2), если 
.
Линии DE и DB вырезают на Парето-оптимальном множестве так называемое переговорное множество DE, т.е. те исходы, о которых партнерам реально стоит договариваться. Среди них выделяется точка Нэша N(n1,n2). Она является решением оптимизационной задачи
,
где (m1,m2) – уровни дохода, которые игроки могут обеспечить себе, не вступая в коалицию.
В данном примере m1= 3, m2 = 3, имеем задачу: Найти максимум выражения
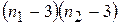, при условии 
(уравнение линии AC).
Можно перейти к одной переменной 
, подставить в функцию и получить 
, решить уравнение 
, откуда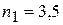 
.
Итак, совместными действиями игроки могут получить результат (3,5; 3,5), что лучше их гарантированного результата без кооперации.
Для достижения этого результата следует решить уравнение
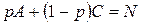
или
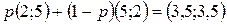
Итак, если муж и жена будут вместе ходить на футбол и балет с вероятностью 0,5, у каждого полезность будет выше, чем при индивидуальном выборе. Реализация этой вероятности 0,5 может быть самая разная. Например, договориться о четных и нечетных неделях, либо бросать монету перед выходом.
|
|
|
Задачи для решения
Найти гарантированные выигрыши игроков без кооперирования, Парето-оптимальное множество, переговорное множество, точку Нэша для задач из темы 4.
|
|
|
