 |
v=dx/dt. dv/dt = -F(x). dv/dx = {-B,0,+B}/v. 1. F(x) = 0; dv/dx = O; v = C(const);. 2. F(x) = - B; dv/dx = - В/v; v dv = - В dx; v2/2 = -Bx + C;
|
|
|
|
v=dx/dt
 |
x
Рис. 5. 2
Фазовые траектории имеют ряд общих черт: они не пересекаются друг с другом (кроме особых точек); перемещение изображающей точки в верхней полуплоскости производится слева направо, а в нижней - справа налево (т. е. по часовой стрелке); пересечение фазовыми траекториями оси абсцисс происходит под прямым углом. На оси абсцисс (при v=0 ) x достигает экстремальных (максимального или минимального значений).
Для исследования нелинейной автоматической системы, описываемой уравнением (5. 2), опишем ее системой дифференциальных уравнений первого порядка
dx/dt = v
dv/dt = -F(x).
Исключив время t из системы получим
dv/dx = - F(x) / v, (5. 3)
или в общем случае: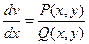 
. (5. 4)
Уравнение (5. 4) представляет собой уравнение фазовых траекторий. Решением этого уравнения является кривая v = f(x), начинающаяся из точки, определяемой начальными условиями (х0, v0), и заканчивающаяся (для устойчивой системы) в особой точке - положении равновесия, определяемой из системы уравнений:
Р(х, у) = 0 Q(x, y) = О.
В линейных системах существует шесть типов особых точек: центр, устойчивый и неустойчивый фокус, устойчивый и неустойчивый узел, " седло".
В нелинейных системах, в отличие от линейных, тип особой точки не всегда определяет поведение изображающей точки на всей фазовой плоскости. Фазовые траектории нелинейной системы могут иметь разный вид в разных областях фазовой плоскости. Фазовые портреты могут содержать: 1) особые точки; 2) сепаратриссы - особые траектории, разделяющие области с траекториями разного типа; 3) предельные циклы - особые траектории, представляющие собой изолированные замкнутые фазовые траектории.
|
|
|
В работе исследуются релейные системы со следующими нелинейными элементами:
F(x) F(x) F(x) F(x)
B B B B
-c c -c c -d -c с d
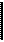
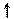
x x x x
- B - B B - B
a) b) c) d)
Рис. 5. 3
Нелинейные элементы относятся к классу кусочно-линейных, принимающих три различных значения: -В, 0, +В на разных участках фазовой плоскости. Решим уравнение (5. 2) для этих трех значений нелинейной характеристики
dv/dx = {-B, 0, +B}/v
1. F(x) = 0; dv/dx = O; v = C(const);
2. F(x) = - B; dv/dx = - В/v; v dv = - В dx; v2/2 = -Bx + C;
3. F(x) = +B; dv/dx = + В/v; v dv = +B dx; v2/2 = +B x + C.
Вид фазовых траекторий для 3-х значений представляет собой параболы и константы, имеющие вид (рис. 5. 4).
|
v
 | |||||
 | |||||
 | |||||
a b c d
|
|
|
 |  | ||||||
 |  |
Рис. 5. 4 Рис. 5. 5
Изображающая точка из положения, определяемого начальными условиями, движется по одной из траекторий, соответствующих значению нелинейной характеристики, меняя вид траектории на линиях переключения, показанных для нелинейностей 3a, b, c, d на рис 5. 5 прямыми, параллельными оси ординат. В замкнутой системе с нелинейностями (рис. 5. 3) возникают незатухающие периодические процессы, и такая система работает неудовлетворительно.
Возникает задача стабилизации релейных систем, которую можно проводить двумя способами: 1) коррекцией по скорости; 2) введением демпфирования - жесткой обратной связи.
Коррекция по скорости проводится согласно схеме рис. 5. 6. Нелинейный элемент с характеристикой F(σ ) имеет линии переключения в виде прямых, параллельных оси ординат в координатных осях σ, v (рис. 5. 5). Построенные же в координатных осях х, v они будут иметь вид прямых, наклоненных к оси ординат на угол γ, причем tgγ =α, что следует из соотношений: σ =x+α v=
{-d, -c, 0, c, d}, или v=-x/α +{-d, -c, 0, c, d}/α (рис. 5. 5).
x s НЭ y 1/p -v 1/p -x
F(s)
- -
a
Рис. 5. 6
(В фигурных скобках показаны все возможные значения для нелинейностей, представленных на рис. 5. 3). Изменение линий переключения приводит к изменению фазовых портретов и стабилизации систем, хотя форма фазовых траекторий не изменится, и будет иметь вид, представленный на рис. 5. 4.
Коррекция жесткой обратной связью проводится согласно схеме рис. 5. 7.
 | |||
| | |||
x НЭ y 1/p -v 1/p -x
F(x)
- -
g
|
|
|
 |
Рис. 5. 7
Уравнение (5. 1), записанное относительно изображений сигналов при подстановке в него передаточной функции линейной части системы рис. 5. 7 W(p) = 1/(р(p+γ )) преобразуется в дифференциальное уравнение, описывающее процессы в системе в виде 
(5. 5)
Запишем систему уравнений: dx/dt=v; dv/dt=-F(x)-γ v, из которой, исключив время, получим дифференциальное уравнение, аналогичное (5. 3):
dv/dx = - (γ v + F(x))/v, или dv v/ ((γ v + F(x)) = -dx,
откуда для трех значений нелинейных функций (рис. 5. 2), легко получить
|
|
|
