Комплексный коэффициент усиления нелинейного звена

Комплексный коэффициент усиления нелинейного звена

При выполнении гипотезы фильтра в схеме учитывается только первая гармоническая составляющая сигнала z(t), т. е.

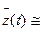  Z_m1sin(ω t+φ ₁)                                        (6. 6)

С использованием формулы Эйлера выражение (6. 6) может быть представлено следующим образом: =Im{Z_m1e^{j (ω t+φ} ₁⁾}=Im{Z}

В то же время выражение (6. 6) может быть записано в виде

        (6. 7)

откуда следует, что Z можно представить как

      

       Комплексным коэффициентом усиления нелинейного звеня (ККУ) называют отношение первых гармоник выходного и входного сигналов, выраженных в комплексной форме. В отличие от линейных звеньев ККУ нелинейного звена зависит не от частоты, а от амплитуды входного сигнала

       (6. 8)

Как видно из (6. 8), комплексный коэффициент определяется коэффициентами K_s и К_c, которые называются коэффициентами гармонической линеаризации.

Определение коэффициентов гармонической линеаризации

       Определение коэффициентов гармонической линеаризации следует проводить, исходя из тех соображений, что сигнал  является приближением сигнала z(t). Учитывая периодичность сигналов, приближение можно проводить на периоде, минимизируя среднюю квадратическую ошибку (СКО) между сигналами z(t) и , т. е.

                                      (6. 9)

Выражения коэффициентов гармонической линеаризации получаются из очевидных соотношений  и имеют вид:

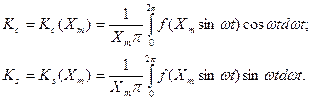           (6. 10)

       Выражения коэффициентов гармонической линеаризации для различных нелинейностей приведены в табл. 6. 2. Следует заметить, что для всех однозначных нелинейных характеристик коэффициенты гармонической линеаризации К_с равны нулю.

Определение параметров автоколебаний по годографам

       Уравнения гармонического баланса (6. 5) с использованием
комплексных коэффициентов усиления линейного и нелинейного звеньев можно записать следующим образом:

W_н(X_m)W_л(jω )=-1                                          (6. 11)

или        W_л(jω )=-1/W_н(X_m)=V_н(X_m).

       Из последнего равенства очевидно, что параметры автоколебаний (частоту ω и амплитуду Х_m) можно найти на пересечении годографа линейной динамической части и инверсного годографа нелинейного элемента, взятого со знаком " минус" (рис. 6. 2). Как видно из рисунка, два годографа пересекаются в двух точках М и N, определяющих возможные автоколебания с параметрами  соответственно.

Рис. 6. 2

Не каждое из найденных решений соответствует устойчивым автоколебаниям, т. е. таким, которые после кратковременного воздействия на систему, восстанавливаются. Для определения устойчивости автоколебаний можно воспользоваться достаточным критерием Гольдфарба, справедливым для устойчивой линейной части системы, который формулируется следующим образом.

           При движении по годографу V(X_m) в сторону увеличения амплитуды Х_m точке пересечения годографов, проходя через которую мы выходим из контура амплитудно-фазовой характеристики линейной части системы, соответствует устойчивое автоколебание. Таким образом, параметры автоколебаний в системе определяются по пересечению двух годографов в точке М.

Определение параметров автоколебаний по логарифмическим характеристикам

       Для определения параметров автоколебаний нелинейных систем с однозначными нелинейностями удобно пользоваться логарифмическими амплитудными и фазовыми характеристиками на основе соотношений, полученных из (6. 11)

       |W_н(X_m)|*|W_л(jω )|=1,

       φ _н(X_m)+φ _л(ω )=-π.                                                (6. 12)

       Из первого соотношения следует | W_л(jω )|=|1/W_н(X_m)| или
с учетом того, что для однозначных нелинейных характеристик К_с=0
| W_л(jω )|=|1/K_s(X_m)|, или после логарифмирования правой и левой частей
                          L_л(ω )=-L_н(X_m),                                                            (6. 13)

где L_л(ω )=20lg|W_л(jω ) |,              -L_н(X_m)=20lg|1/K_s(X_m)|.

       Из второго соотношения для однозначных нелинейных
характеристик, для которых φ _н(X_m)=0, следует φ _л(ω )=-π.                (6. 14)

       Таким образом, равенства (6. 13) и (6. 14) определяют условия возникновения автоколебаний и из них могут быть найдены параметры возможных автоколебаний. Однако не всякое решение соответствует устойчивым автоколебаниям. Для определения устойчивости автоколебаний пользуются следующими правилами:

1. если при увеличении амплитуды Х_m ординаты логарифмической характеристики –L_н(X_m) увеличиваются, то линия “ -π ” штрихуется сверху, а в противном случае - снизу;

2. если при увеличении частоты ω фазовая характеристика линейной части φ _л(ω ) пересекает прямую " -π ", переходя с заштрихованной стороны на незаштрихованную, то автоколебания - устойчивы, а в противном случае - неустойчивы.

       Таким образом, для определения параметров автоколебаний в замкнутой системе с нелинейным элементом, имеющим однозначную характеристику, на одном графике строятся характеристики L_л(ω ) и -L_н(X_m) (очевидно, что ω и Х_m откладываются на разных участках однойоси абсцисс в логарифмическом масштабе); фиксируется точка ω ₀, для которой выполняется условие (6. 14) и из равенства (6. 13) определяется амплитуда Х_m0 возможных автоколебаний; проверяется устойчивость автоколебаний.

На рис. 6. 3 показан пример определения параметров автоколебаний в замкнутой системе с нелинейностью типа " насыщение", коэффициенты гармонической линеаризации которой приведены в табл. 6. 2.

 

          

Рис. 6. 3

           В лабораторной работе исследуется автономная нелинейная система (рис. 6. 1), линейная часть которой задана в лабораторной работе № 2 с нелинейностью, заданной в табл. 6. 1 с параметрами, соответствующими номеру бригады. При этом для неоднозначной нелинейной характеристики рекомендуется пользоваться построением годографов, а для однозначной - логарифмических характеристик линейной и нелинейной частей разомкнутой системы.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: