 |
1. F(x) = 0; dv/dx = -g; v = - g x + const ;
|
|
|
|
1. F(x) = 0; dv/dx = -g; v = - g x + const;
2. F(x) = - B; dv v/ (g v - B) = - dx;
v + ln ½ g v - B½ = - x + const;
3. F(x) = +B; dv v/ (g v + B) = - dx;
v - ln ½ g v + B½ = - x + const.
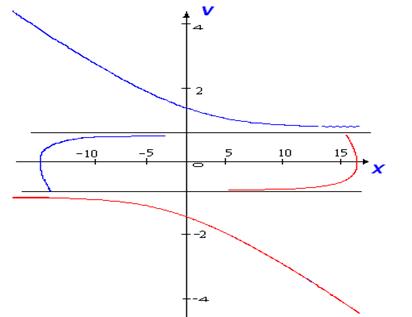
Вид фазовых траекторий (для случаев 2 и 3 ) может быть получен графическим суммированием относительно v двух графиков: х= -v/γ и x = - B/γ 2 ln|γ v - B| (для - B );
х = -v/γ и х = +-В/γ 2 ln|γ v+B| (для +-В ).
Очевидно, что фазовые траектории при этом изменятся, что приведет к стабилизации замкнутой нелинейной системы, хотя линии переключения останутся прежними, параллельными оси ординат. На рис. 5. 8 представлены фазовые траектории для B=0. 25, g=0. 3.
|
, Рис. 5. 8
В нелинейных системах возможен режим, называемый скользящим режимом, когда фазовые траектории подходят к линии переключения так, как показано на рис. 5. 9. В этом режиме релейные элементы находятся в вибрационном режиме, а изображающая точка перемещается по линии переключения.
v
.
 |
x
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
Рис. 5. 9
Подготовка к работе
1. Для нелинейных характеристик и начальных значений, заданных в табл. 1 в соответствии с номером бригады, нарисовать вид фазовых траекторий для процессов в замкнутых системах рис. 5. 1 (без коррекции), рис. 5, 6 (с коррекцией по скорости), рис. 5. 7 (с коррекцией жесткой обратной связью). Принять B=0, 25; с=0, 1; d=0, 2.
|
|
|
2. Для указанных нелинейностей найти значение коэффициента α, при котором возникает скользящий режим, и зарисовать соответствующий фазовый портрет.
Задание на выполнение работы
1. Смоделировать замкнутую нелинейную систему 2-го порядка (рис. 5. 1). Для двух нелинейностей и начальных условий, заданных в табл. 5. 1 в соответствии с номером бригады, наблюдать и зарисовать фазовые портреты и переходные процессы x(t), v(t).
2. Смоделировать замкнутую нелинейную систему с коррекцией по скорости (рис. 5. 6), установив значения α, заданные в табл. 5. 1.
3. Подобрать значение α, при котором имеет место скользящий режим. Наблюдать и зарисовать фазовые портреты и переходные процессы x(t), v(t) и y(t).
4. Смоделировать замкнутую нелинейную систему с коррекцией жесткой обратной связью (рис. 5. 7), установив значения γ, заданные в табл. 5. 1. Наблюдать и зарисовать фазовые портреты и переходные процессы x(t), v(t).
5. Сделать выводы о влиянии значений α и γ на переходные процессы в системе.
Таблица 5. 1
| № бригады | нелинейность | X(0) V(0) | a | g |
| a, c | 0. 5 0. 8 | 0. 3 0. 6 | 0. 2 0. 8 | |
| a, d | 0. 0 0. 5 | 0. 5 0. 2 | 0. 3 0. 7 | |
| b, c | 0. 8 0. 0 | 0. 4 0. 8 | 0. 25 0. 75 | |
| b, d | 0. 7 0. 7 | 0. 7 0. 35 | 0. 4 0. 9 | |
| a, b | 1. 0 0. 0 | 0. 5 1. 0 | 0. 3 1. 0 | |
| c, d | 0. 0 1. 0 | 0. 75 0. 25 | 0. 5 1. 0 | |
| a, d | 0. 75 0. 25 | 0. 3 0. 5 | 0. 4 0. 9 | |
| b, c | 0. 3 0. 5 | 0. 5 0. 8 | 0. 25 1. 0 | |
| b, d | 0. 5 0. 8 | 0. 2 1. 0 | 0. 4 1. 0 | |
| b, c | 0. 2 1. 0 | 0. 5 0. 75 | 0. 5 0. 2 | |
| a, b | 0. 4 -0. 5 | 0. 35 0. 8 | 0. 3 0. 9 | |
| a, c | -0. 8 -1. 0 | 0. 45 0. 7 | 0. 55 0. 8 | |
| c, d | 0. 75 -0. 5 | 0. 6 0. 4 | 0. 45 0. 6 | |
| a, d | -1. 0 -1. 0 | 0. 85 0. 2 | 0. 35 0. 7 | |
| b, c | 0. 9 -0. 5 | 0. 45 0. 9 | 0. 25 0. 8 |
Контрольные вопросы
|
|
|
- Дайте определение фазовой плоскости, фазовой траектории, фазового портрета, изображающей точки особых точек, особых траекторий.
- Каковы свойства фазовой плоскости, представленной на рис. 5. 2.
- Выведите уравнения фазовых траекторий при коррекции по скорости и с помощью жесткой обратной связи.
- Как выглядят линии переключения для нелинейных элементов, представленных на рис. 5. 3, при коррекции по скорости и с помощью жесткой обратной связи.
- Что такое скользящий режим и когда он возникает?
Литература
1. Теория автоматического управления. Ч. II. Под ред. Нетушила А. В., М.: Высш. школа, 1982, 400 c.
ЛАБОРАТОРНАЯ РАБОТА № 6
Исследование нелинейных систем автоматического управления методом гармонического баланса
Цель работы: исследование периодических процессов в автономных нелинейных системах автоматического управление (автоколебаний), условий возникновения устойчивых автоколебаний иопределение их параметров.
Теоретические положения
Рассматривается нелинейная система, структурная схема которой представлена на рис. 6. 1,
xy=0 x(t) z(t) y(t)
+ f(x) Wн(p)
-
 |
Рис. 6. 1
где f(х) - характеристика статического нелинейного элемента, W(p) -передаточная функция линейной динамической части системы автоматического управления. Из схемы (рис. 6. 1) при xy=0 следует
х(t) +y(t)=0. (6. 1)
Для анализа периодических процессов, протекающих в схеме,
предположим, что сигнал ошибки x(t) можно представить в виде
гармонического сигнала, т. е. x(t)=Xm sinω t. (6. 2)
Тогда на выходе нелинейного элемента сигнал можно представить рядом Фурье
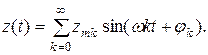(6. 3)
Для нелинейных элементов с нечетными характеристиками постоянная составляющая сигнала z(t) (zmo) равна нулю и суммирование в (6. 3), начинается с к=1. В зависимости от вида нелинейности соотношение амплитуд гармонических составляющих в (6. 3) будет различным. При прохождении сигнала z(t) через линейное динамическое звено соотношение амплитуд гармонических составляющих изменится, при этом амплитуды высших гармоник уменьшатся из-за фильтрующих свойств линейной части системы. В методе гармонического баланса принимается гипотеза фильтра, согласно которой всеми гармоническими составляющими сигнала y(t), кроме первой, можно пренебречь. При выполнении гипотезы фильтра
|
|
|
y(t)=Ym1sin(ω t+φ ) (6. 4)
и равенство (6. 1) распадается на два:
Xm=Ym1; φ =π. (6. 5)
Уравнения (6. 5) носят название уравнений гармонического баланса.
|
|
|
