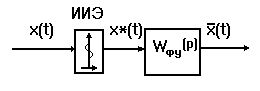Контрольные вопросы. Литература. Лабораторная работа № 4. Исследование линейных импульсных автоматических систем. Теоретические положения

Контрольные вопросы

1. Каковы алгоритмы выбора последовательного, параллельного и корректирующего устройства в цепи обратной связи?

2. Из каких соображений строится ЛАЧХ желаемой (скорректированной) системы?

3. Что такое кинетическая ошибка системы, как она вычисляется и от чего зависит? Как снять значение кинетической ошибки при цифровом моделировании скорректированной системы?

4. С помощью каких физических элементов можно реализовать построенные вами  корректирующие устройства? Каковы параметры этих элементов?

5. Опишите порядок построения логарифмических частотных характеристик корректирующих устройств при последовательной, параллельной и коррекции с обратной связью.

 

Литература

. 1. Теория автоматического управления. Ч. I. Под ред. Нетушила А. В., М.: Высш. школа, 1982, 400 c.

ЛАБОРАТОРНАЯ РАБОТА № 4

Исследование линейных импульсных автоматических систем

       Цель работы: исследование особенностей динамических процессов в импульсных системах, связанных с квантованием по времени, осуществляемым импульсным элементом; изучение вопросов устойчивости импульсных систем, приобретение навыков исследования временных и частотных характеристик импульсных систем.

 

Теоретические положения

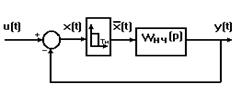
       В работе рассматриваются процессы, протекающие в замкнутой импульсной системе, представленной на рис. 4. 1 с импульсным элементом (ИЭ), вырабатывающим последовательность импульсов, модулированную значениями сигнала отклонения (ошибки) системы x(t), в дискретные моменты времени (mТ, m=O, l,... N) и имеющую вид рис. 4. 2, где Т - период квантования, Ти - продолжительность импульса.

 

 

                       ИЭ     

 

Рис. 4. 1                                                    Рис. 4. 2

 

 

           Сигнал 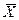(t)можно представить как выход идеального импульсного элемента (ИИЭ), вырабатывающего модулированную сигналом отклонения (ошибки) последовательность δ - функций x*(t), пропущенную через формирующее устройство с передаточной функцией

 

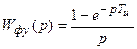  (рис. 4. 3).

 

               

 

               

 

                                          Рис. 4. 3

           Тогда замкнутая система рис. 4. 1 может быть представлена структурной схемой рис. 4. 4 (а и б).

Y*(t)

X*(t)

     Рис. 4. а

	U*(t)

 

                            -   

                                                                             

Рис. 4. 4б

           На рис. 4. 4 W_p*(p)) - дискретная передаточная функция разомкнутой импульсной системы, которая может быть получена из непрерывной передаточной функции с использованием следующего перехода:

Wp(p)=Wфи(р)Wнч(р

 

где L - непрерывное, D - дискретное преобразование Лапласа; Т – период квантования.

           Проделаем этот переход для ,

          

,

где n - степень полинома А(р); p₁, p₂, … p_n - корни полинома А(р);

c_-1, c₀, c₁, …, c_n - коэффициенты, которые могут быть найдены методом неопределенных коэффициентов или по формуле разложения.

       Весовая функция, соответствующая выражению в фигурных скобках, может быть записана в виде:

 

;

,

 

откуда легко получить:

 

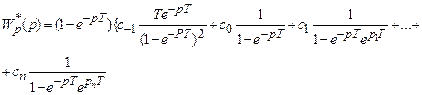
           Приведением к общему знаменателю это выражение можно представить в виде отношения двух полиномов, а именно:

 

,

где n - степень полиномов.

           Передаточные функции замкнутой импульсной системы с единичной обратной связью (рис. 4. 4) можно рассчитать по формулам:

, ,

где А*(р) - характеристический полином замкнутой системы степени n вида     

.

           С использованием этих передаточных функций можно рассчитать установившиеся значения ошибок х_уст на основании предельной теоремы дискретного преобразования Лапласа

 

,

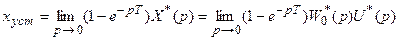где U*(p) - дискретное преобразование Лапласа от входного сигнала.

       По передаточной функции замкнутой системы можно найти выходной сигнал в дискретные моменты времени с использованием разностного уравнения. При нулевых значениях входного и выходного сигналов для отрицательных моментов времени его можно получить из уравнения, записанного в изображениях с использованием дискретного преобразования Лапласа, которое имеет вид

;

или

Из вышеприведенного уравнения можно записать разностное уравнение:

или

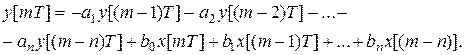
           Используя характеристическое уравнение замкнутой импульсной системы А*(р) и производя подстановку

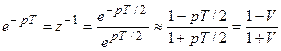
получаем характеристическое уравнение относительно переменной V (A(V)=0), для которого можно использовать критерий Гурвица, сформулированный  для непрерывных систем.

       По дискретной передаточной функции разомкнутой импульсной системы могут быть получены выражения комплексного коэффициента усиления импульсной разомкнутой САР. Для этого в выражении W_p*(p) должна быть произведена замена оператора р на комплексное число jω и использована формула Эйлера

.

Годограф разомкнутой импульсной системы строится при изменении ω в диапазоне [0, ω ₀/2], где ω ₀ = 2π /Т - частота квантования сигнала. На рис. 4. 5 представлен пример годографа разомкнутой импульсной системы.

Годограф не охватывает точку с координатами (-1; j₀) и, следовательно, в соответствии с критерием Найквиста для устойчивой разомкнутой системы, соответствующая замкнутая импульсная система - устойчива и обладает некоторым запасом устойчивости по амплитуде Δ А, по которому можно найти значение предельного коэффициента усиления К_пред, с использованием пропорции:

К ~ (1-Δ А)

К_пред  ~   1.  

Коэффициент усиления разомкнутой импульсной системы определяется, исходя из следующих соотношений:

 

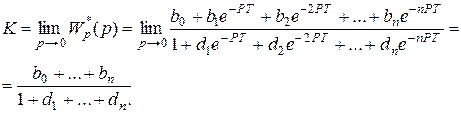
⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: