Литература. Лабораторная работа № 3. Коррекция систем автоматического управления. Теоретические положения

Литература

. 1. Теория автоматического управления. Ч. I. Под ред. Нетушила А. В., М.: Высш. школа, 1982, 400 c.

2 Ягодкина Т. В., Хризолитова С. А., Применение Mathcad для решения задач теории автоматического управления, Учебное пособие. М.: Изд-во МЭИ, 2004. – 52 с.

ЛАБОРАТОРНАЯ РАБОТА № 3

Коррекция систем автоматического управления

       Цель работы: исследование качества переходного процесса САУ с последовательными, параллельными корректирующими устройствами и корректирующими устройствами в цепи обратной связи.

Теоретические положения

               

Для того чтобы система удовлетворяла требуемым показателям качества необходимо, как правило, введение в систему дополнительных связей или дополнительных корректирующих устройств. Из различных методов синтеза широко используются частотные характеристики, по которым исследуются устойчивость и качество переходного процесса, а также проводится выбор корректирующих устройств. Во многих случаях наиболее удобно применять логарифмические амплитудные и фазовые частотные характеристики разомкнутой системы. Причём, при исследовании минимально-фазовых систем достаточно получить только одну амплитудную частотную характеристику. Фазовая частотная характеристика таких систем однозначно определяется их амплитудной характеристикой и наоборот.

Задача синтеза сводится к определению передаточной функции корректирующего устройства W_ку(p) в системе и места включения КУ. По месту включения корректирующего устройства в системе существуют три вида коррекции: последовательная, параллельная и коррекция с помощью обратной связи. Для выбора корректирующего устройства необходимо:

1. Построить ЛАЧХ и ЛФЧХ исходной системы

       L_исх(ω ) = 20lg│ W_{p исх}(jω )│ φ _исх(ω ) = argW_{p исх}(jω ).

2. Если исходная система не удовлетворяет заданным параметрам качества (см. лабораторную работу № 2), построить желаемую ЛАЧХ или ЛАЧХ скорректированной системы L_CK(ω ).

       Построение желаемой ЛАЧХ скорректированной системы осуществляется с учётом следующих соображений:

- наклоны участков ЛАЧХ в области низких и высоких частот для скорректированной системы равны наклонам соответствующих участков ЛАЧХ исходной системы (исключением является случай, когда жёсткая обратная связь охватывает интегрирующее звено);

- при построении низкочастотного участка желаемой ЛАЧХ следует учесть коэффициент усиления разомкнутой системы, который определяет ошибку системы в установившемся режиме, а его наклон определяется степенью астатизма системы ν (ν - разность числа интегрирующих и дифференцирующих звеньев). Величина частоты среза выбирается с учётом соотношения

- t_рег ≤ kπ /ω _c, где k=f(σ ) [ 1 ];

- на частоте среза ω _c наклон желаемой ЛАЧХ необходимо задавать равным -20дб/дек. Протяжённость среднечастотного участка слева и справа от частоты среза должна быть равна 0. 4 - 0. 8 декады, что позволит обеспечить достаточный запас устойчивости по фазе и требуемое качество переходного процесса.

Желаемая ЛАЧХ скорректированной системы должна в возможно большем диапазоне частот совпадать с ЛАЧХ исходной системы, чтобы не усложнялась реализация корректирующего устройства. Если в качестве желаемой ЛАЧХ скорректированной системы может быть выбрана типовая ЛАЧХ, соответствующая системе, имеющей передаточную функцию вида:

 

,                                           (3. 1)

где К> 1; Т₁> Т₂> Т₃; α = 1 - 2; β = 1 - 2, то для её более точного построения можно использовать номограммы связи параметров ЛАЧХ разомкнутой системы с показателями качества процесса управления в замкнутой системе. В этом случае по заданным величинам быстродействия t_рег, перерегулирования σ находят ω ₁/ω _c  и ω ₃/ω _c (рис. 3. 1).

 

 

Рис. 3. 1

 

           При построении желаемой ЛАЧХ можно использовать и другие номограммы и графики, которые дают связь между параметрами частотных характеристик и показателями качества. По виду L_CK(ω ) восстанавливается передаточная функция скорректированной разомкнутой системы и строится ЛФЧХ φ _ск(ω ). По логарифмическим характеристикам L_CK(ω ) и φ _ск(ω ) определяют запасы устойчивости и ошибку в установившемся режиме. Прямые показатели качества системы можно определить по переходной характеристике, построенной с помощью моделирования замкнутой системы на ЭВМ.

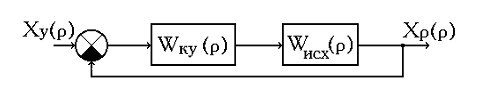       В конечном итоге задача синтеза сводится к выбору параметров соответствующих корректирующих устройств, обеспечивающих достижение заданного качества переходного процесса в замкнутой системе. При последовательной коррекции корректирующее устройство включается в прямую цепь так, как показано на рис. 3. 2.

Рис. 3. 2

           Соотношения для логарифмических частотных характеристик скорректированной системы следуют из очевидного равенства для

разомкнутой системы  и имеют вид

. (3. 2)           Из (3. 2) следует основное соотношение для определения L_ку(ω )
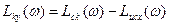                                      .                (3. 3)

Графические построения при последовательной коррекции представлены на рис. 3. 3.

 

Рис. 3. 3

           Далее по виду найденной ЛАЧХ корректирующего устройства (рис. 3. 3) определяется структура и параметры звена, включённого в прямую цепь управления.

       При параллельной коррекции корректирующее устройство включается параллельно какому-нибудь устройству исходной САУ (рис. 3. 4).

Рис. 3. 4

 

           Для параллельной коррекции справедливы следующие соотношения:

(3. 4)

Обозначим                                .

 

Тогда из (3. 4)                           ;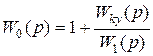

 

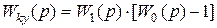                                               .        (3. 5)               

       Соотношения для логарифмических частотных характеристик скорректированной разомкнутой системы (рис. 3. 4) следуют из равенства:

                           и имеют вид:

,       .

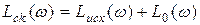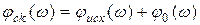           Из вышеизложенного следует порядок определения ЛАЧХ параллельного корректирующего устройства, заключающийся в построении L₀(ω ) по аналогии с построением L_ky(ω ) при последовательной коррекции, восстановлении передаточной функции W₀(p) по L₀(ω ) и определении W_ky(ω ) из соотношения (3. 5).

       При коррекции с помощью обратной связи (ОС) корректирующее устройство охватывает одно или несколько устройств исходной САУ. Обычно обратной связью охватываются устройства системы, которые обладают наибольшими постоянными времени и имеют недостаточно стабильные, нелинейные характеристики (рис. 3. 5).

 

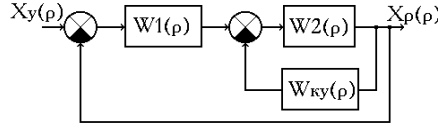
Рис. 3. 5

           В этом случае также используется графический метод на основе построения ЛАЧХ. Задача синтеза звена обратной связи решается несколько сложнее, чем в случае последовательного корректирующего устройства.

       Передаточная функция разомкнутой скорректированной системы имеет вид

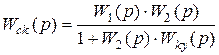                                          ,                (3. 6)

где W₂(p), W_ky(p) - передаточные функции части системы, охватываемой обратной связью и корректирующего устройства соответственно;

W₁(p) -      передаточная функция части системы, не охваченной корректирующей обратной связью.

 

       Рассматриваются две области частот, когда

           < < 1 и > > 1. В первом случае коррекция не оказывает существенного влияния на характеристики исходной системы и можно считать, что L_ск(ω ) ≈ L_исх(ω ) и φ _ск(ω ) ≈ φ _исх(ω ). Для второй частотной области справедливы следующие приближённые выражения:

           ,

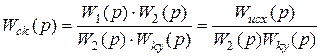откуда следуют соотношения:

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: