 |
Полимолекулярная адсорбция
|
|
|
|
Если адсорбция протекает с образованием полимолекулярного адсорбционного слоя, то изотерма адсорбции отличается от ленгмюровской (рис. 76) и имеет более сложный вид (рис. 77).
С. Брунауэр, П. Эммет и Е. Теллер (1935–1940) создали теорию полимолекулярной адсорбции (сокращенно – теорию БЭТ). Используя ряд положений теории Ленгмюра, они сделали дополнительное допущение о возможности образовании на поверхности адсорбента комплексов между адсорбционным центром и одной, двумя, тремя и большим числом молекул адсорбента. В этой теории процесс адсорбции рассматривается как ряд последовательных квазихимических реакций со своими константами равновесия. На активных центрах поверхности адсорбента могут образоваться конденсированные полимолекулярные слои.
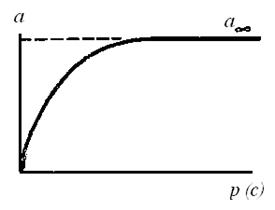
Рис. 76. Изотерма адсорбции Ленгмюра
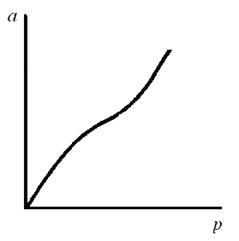
Рис. 77. Изотерма полимолекулярной адсорбции
Согласно теории БЭТ при температуре ниже критической каждая молекула, адсорбированная в первом слое, является активным центром для молекул, образующих второй слой адсорбата, а дифференциальная теплота адсорбции qа во всех слоях, кроме первого, равна теплоте конденсации Δ Н к. В результате авторами было получено уравнение изотермы адсорбции теории БЭТ:
 ,
| (333) |
где с = exp[(qa – Δ Н к)/ RT ] и а ∞ – константа, р – равновесное и давление адсорбата.
Уравнение (333) в координатах а – p/ps соответствует s-образной кривой, а в координатах p/ps –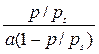 
– прямой линии (рис. 78). При 0,05 < p/ps< 0,30 по наклону этой прямой можно графически определить предельную адсорбцию а ∞. Теория БЭТ позволяет также определить площадь, занимаемую одной молекулой адсорбата в адсорбционном слое (уравнение 318).
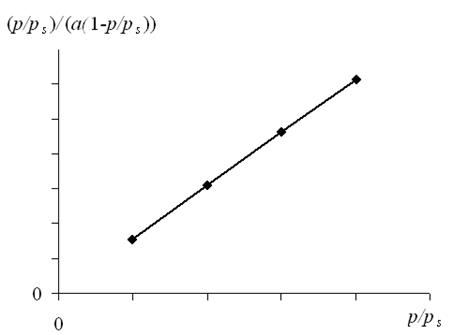
Рис. 78. Изотерма полимолекулярной адсорбции в линейном виде
|
|
|
Уравнение полимолекулярной адсорбции широко применяется для определения удельной поверхности адсорбентов.
Капиллярная конденсация
Конденсацию паров смачивающей жидкости в капиллярах твердого тела называют капиллярной конденсацией. Пар может конденсироваться лишь при температуре ниже критической. Когда пар над мениском достигает насыщения, начинается конденсация и поры адсорбента заполняются жидкостью. Если образующаяся жидкость хорошо смачивает стенки капилляров, то есть поверхность адсорбента, то в капиллярах образуются вогнутые мениски.
Изотермы сорбции при капиллярной конденсации имеют S -образную форму (рис. 79). Характерные особенности таких изотерм заключаются в том, что вначале на кривой намечается некоторый предел адсорбции (почти горизонтальный участок), но при достижении определенного давления кривая резко идет вверх, что говорит о быстром возрастании количества поглощенного пара в результате капиллярной конденсации. И еще одна особенность состоит в несовпадении изотерм сорбции и десорбции, то есть в наличии сорбционного гистерезиса. Это означает, что одному и тому же давлению пара отвечают разные величины сорбции в зависимости от направления процесса. Явление гистерезиса объясняется главным образом наличием следов воздуха в порах, препятствующего полному смачиванию их стенок, разнообразием формы и радиусов капилляров.
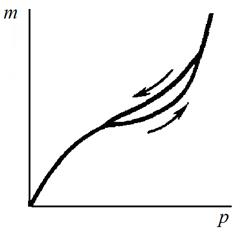
Рис. 79. Изотерма сорбции при капиллярной конденсации (m – масса поглощенных сорбентом паров, р – равновесное давление)
Конденсация пара адсорбата в капиллярах на вогнутой поверхности жидкости (жидкий адсорбат смачивает поверхность капилляра) происходит при давлении пара более низком, чем давление насыщенного пара адсорбата над плоской поверхностью жидкости. Причиной этого является различие гидростатических давлений по обе стороны мениска жидкости.
|
|
|
На искривленной поверхности жидкости возникает так называемое капиллярное давление (рис. 80). Оно равно разности гидростатических давлений между точкой, расположенной в фазе (в данном случае – газ), к которой мениск обращен вогнутой стороной, и точкой, расположенной в фазе (в данном случае – жидкость), к которой мениск обращен выпуклой стороной и определяется уравнением Лапласа для капиллярного давления (334):
 ,
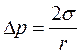| (334) |
где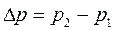 
; r – радиус кривизны сферического мениска жидкого адсорбата в капилляре.
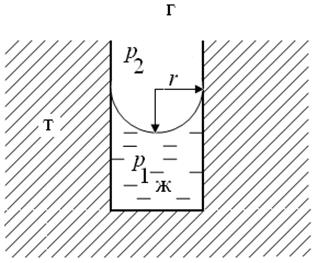
Рис. 80. Схема, иллюстрирующая возникновение капиллярного давления, где p 2 и p 1 – давление в газовой (жидкой) и жидкой фазе соответственно,
r – радиус кривизны сферического мениска в капилляре
Пониженное гидростатическое давление жидкости под ее вогнутым мениском приводит к пониженному давлению ее насыщенного пара по сравнению с давлением насыщенного ее пара над плоской поверхностью этой же жидкости.
Связь между радиусом r вогнутого сферического мениска, образовавшегося в капилляре и давлением насыщенного пара рr жидкости над этим мениском дается уравнением Томсона – Кельвина,
 ,
| (335) |
где р s – давление насыщенного пара над плоской поверхностью жидкости; σ – поверхностное натяжение жидкости; V – мольный объем жидкости; R – газовая постоянная; Т – абсолютная температура.
Если мениск имеет цилиндрическую форму, уравнение (335) принимает вид
 ,
| (336) |
где r – радиус кривизны цилиндрического мениска жидкого адсорбата в капилляре.
Сравнение уравнений (335) и (336) показывает, что давление пара адсорбата над цилиндрическим мениском жидкости всегда больше, чем над сферическим мениском той же жидкости с тем же радиусом, однако оба эти давления меньше, чем давление насыщенного пара над плоской поверхностью этой же жидкости. Это соотношение позволяет объяснить капиллярную конденсацию.
Уравнение Томсона – Кельвина является основным при расчетах, связанных с явлениями капиллярной конденсации. Если известны давление насыщенного пара жидкости над плоской поверхностью рs, и радиус капилляров адсорбента, то по уравнению Томсона – Кельвина можно вычислить давление пара р, выше которого в капиллярах начинается конденсация на их цилиндрических стенках (уравнение (336)), а затем десорбция с вогнутого сферического мениска (уравнение (335)).
|
|
|
|
|
|
