 |
Исследование частотных характеристик контура
|
|
|
|
2.2.1. Включить ЭВМ и запустить предложенную преподавателем программу.
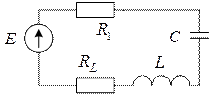2.2.2. Смоделировать на наборном поле программы электрическую цепь с максимальной добротностью 
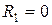. Здесь 
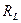- активное сопротивление, которое всегда имеется у реальной катушки индуктивности.
2.2.3. Запустить программу на выполнение в режиме расчёта частотных характеристик. Установить начальный диапазон расчёта от 1000 Гц (верхняя граница) до 10 Гц (нижняя граница). Задать построение графика тока 
в зависимости от логарифма частоты.
2.2.4. Проанализировать график и уточнить диапазон частот, при котором график наиболее информативен. Скопировать график в протокол.
2.2.5. В выбранном диапазоне частот построить графики напряжения на ёмкости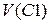 
, идеальной индуктивности 
и активной составляющей сопротивления индуктивности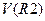 
. Скопировать графики в протокол.
2.2.6. В выбранном диапазоне частот построить график фазы тока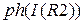 
. Скопировать график в протокол.
2.2.7. Повторить испытания по пп. 2.2.2 - 2.2.5 для таких значений сопротивления R1, при которых добротность контура равна 1 и 2.
Определение параметров цепи в установившемся режиме
2.3.1. Смоделировать на наборном поле программы электрическую цепь с добротностью Q=1.
2.3.2. Запустить программу на выполнение в режиме расчёта цепей переменного тока. Задать частоту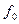 
, соответствующую резонансу. Определить значения тока, напряжений во всех узлах цепи, мощностей всех элементов. Скопировать данные в протокол.
2.3.3. Повторить исследования по п. 3.3.2 для частот 
и 
.
Аналитические исследования
3.1. Дать анализ графиков по пп. 2.2.4-2.2.6. Объяснить вид каждой кривой. Определить по графику полосу пропускания колебательного контура.
3.2. Сопоставить графики по пп. 2.2.5 и 2.2.7. Объяснить изменение графиков в связи с изменением добротности контура.
|
|
|
3.3. Построить векторные и топографические диаграммы токов и напряжений по пп. 2.3.2 и 2.3.3. Объяснить диаграммы.
3.4. Составить баланс мощностей по пп. 2.3.2 и 2.3.3.
Вопросы для самопроверки
1. Определить полное, активное, реактивное и волновое сопротивление контура.
2. Определить условие возникновения резонанса.
3. Как различают резонанс напряжений и резонанс токов?
4. Что такое волновое сопротивление и добротность контура?
5. Как влияет величина добротности на резонансные свойства контура?
6. Как определяют полосу пропускания контура?
Лабораторная работа № 8
Исследование частотных свойств параллельного контура
Цель работы:
виртуально: изучение частотных характеристик цепи с параллельным соединением элементов R, L, C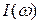 
, 
, 
, 
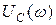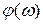при различных добротностях контура;
аналитически: определение полного и волнового сопротивления контура, определение добротности и полосы пропускания контура, определение сдвига фаз между напряжением и током в контуре.
Основы теории
При изучении теории обратить внимание на следующее.
Полная проводимость параллельной цепи в комплексном виде равна комплексной сумме активных и реактивных составляющих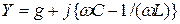 
. Полная проводимость цепи в алгебраическом виде имеет вид
.
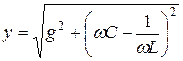Анализ последнего уравнения показывает, что, возможно, такое состояние цепи, когда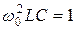 
. При этом общая проводимость цепи оказывается минимальной численно равной активной проводимости. Указанное состояние цепи названо резонансом, а частота 
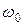- резонансной.
При частотах ниже резонансной ёмкостная проводимость оказывается меньше, чем проводимость индуктивности. Цепь ведёт себя как активно – индуктивная нагрузка, при которой ток отстаёт от напряжения на некоторый угол. При частотах выше резонансной проводимость ёмкости оказывается больше, чем проводимость индуктивности. При этом цепь ведёт себя как активно – ёмкостная нагрузка, при которой ток опережает напряжение на некоторый угол. При резонансе токи индуктивности и ёмкости взаимно компенсируют друг друга, цепь в целом проявляет себя как активный элемент со сдвигом фаз между током и напряжением равным нулю.
|
|
|
Так как проводимость цепи при резонансе минимальна, то напряжение в цепи (если ток на входе цепи поддерживается независимым от свойств цепи) при резонансе принимает максимально возможное значение. Соответственно возросшему напряжению на индуктивности и ёмкости возможны перенапряжения. Для оценки перенапряжений можно использовать понятие волновой проводимости 
и добротности 
. Так как при резонансе ток на активном сопротивлении численно равен току источника, то добротность показывает, во сколько раз реактивный ток при резонансе превышает ток источника.
Параллельный колебательный контур часто используется в цепях передачи информации для пропускания (или, наоборот, исключения) сигналов определённых частот. Характеристикой контура является полоса пропускания частот. Полоса пропускания частот, это диапазон частот, при котором сигнал, проходя через цепь, ослабляется по мощности не более чем в два раза. Полосу пропускания частот удобно определять по кривой изменения напряжения (или тока на активном сопротивлении). В полосе пропускания частот напряжение больше или равно 0.707 от напряжения резонанса.
Так как на краях полосы пропускания напряжение уменьшается в 
раз, делаем вывод, что для этого алгебраическое значение проводимости должно быть в раз выше активной проводимости 
. Решая уравнение можно определить нижнюю и верхнюю границы частот полосы пропускания контура.
Раскрывая скобки, выражая активную проводимость через волновую проводимость и добротность контура, получаем полосу пропускания контура в виде 
.
Виртуальные исследования
Предварительные расчёты
На основании данных параметров элементов исследуемой цепи определить: собственную частоту колебаний контура, волновое сопротивление контура, максимально возможную добротность контура (когда активное сопротивление 
контура равно бесконечности).
|
|
|
|
|
|
