 |
Исследование частотных характеристик контура
|
|
|
|
2.2.1. Включить ЭВМ и запустить предложенную преподавателем программу.
2.2.2. Смоделировать на наборном поле программы электрическую цепь. Установить напряжение источника равным 1 В, начальную фазу напряжения нулевой.
2.2.3. Запустить программу на выполнение в режиме расчёта частотных характеристик. Установить начальный диапазон расчёта от 20 кГц (верхняя граница) до 10 Гц (нижняя граница). Задать построение графика тока 
в зависимости от логарифма частоты.
2.2.4. Проанализировать график и уточнить диапазон частот, при котором график наиболее информативен. Скопировать график в протокол.
2.2.5. В выбранном диапазоне частот построить графики напряжения на ёмкости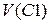 
, идеальной индуктивности 
и активном сопротивлении нагрузки 
. Скопировать график в протокол.
2.2.6. В выбранном диапазоне частот построить график фазы тока 
. Скопировать график в протокол.
2.2.7. Повторить испытания по пп.2.2.2 – 2.2.6 для коэффициента связи катушек индуктивности 
и 
Аналитические исследования
3.1. Дать анализ графиков по пп. 2.2.3 -2.2.6. Объяснить вид каждой кривой. Определить по графику полосу пропускания колебательного контура.
3.2. Сопоставить графики по пп. 2.2.7. Объяснить изменение графиков в связи с изменением коэффициента связи контуров.
Вопросы для самопроверки
1. Как определить полную, активную, реактивную проводимость индуктивно – связанной цепи?
2. Как определить условие возникновения резонанса в индуктивно - связанной цепи?
3. Как влияет коэффициент связи контуров на условие возникновения резонанса?
4. Что такое волновое сопротивление и добротность контура?
5. Как влияет величина добротности на резонансные свойства контура?
6. Как определяют полосу пропускания контура?
|
|
|
Лабораторная работа № 10
Исследование переходных процессов в электрических цепях
Цель работы
виртуально: моделирование простейших электрических цепей с одним, двумя и тремя накопителями энергии (L, С элементы);
аналитически: математическое исследование влияния параметров цепи и числа накопителей энергии на вид переходного процесса.
Основы теории
При изучении теории обратить внимание на следующее.
Электромагнитная энергия поля инерционна и потому не может изменяться мгновенно. Как следствие мгновенно не может измениться индуктивный ток (энергия поля катушки индуктивности 
) и ёмкостное напряжение (энергия поля конденсатора 
). Полагая, что процессы изменения топологии электрической цепи происходят очень быстро, указанные следствия записывают в виде законов коммутации 
и 
. Здесь t(0-) означает момент времени до коммутации, t(0+) - момент времени после коммутации, причём t(0+)-t(0-)=0.
Для мгновенных значений напряжений и токов переходного процесса справедливы законы Кирхгофа и соответствующие методы составления системы уравнений цепи.
Если воспользоваться методом исключений переменных в полученной системе уравнений, то исследуемый ток (в конечном итоге) запишется в виде дифференциального уравнения n порядка. Порядок дифференциального уравнения определяется количеством инерционных элементов. Для цепи с одним элементом L или C уравнение тока имеет вид 
, для цепи с двумя инерционными элементами - 
, для цепи с тремя инерционными элементов - 
и т.д.
Общим решением дифференциального уравнения n порядка является сумма из n членов вида 
, 
- корни характеристического уравнения от полученного выше дифференциального уравнения. Корни уравнения могут быть мнимыми сопряжёнными, комплексными сопряжёнными и отрицательными действительными. Вот почему кривые изменения напряжения и тока при переходных процессах имеют самую разнообразную форму от простой экспоненты до синусоиды.
|
|
|
Рассмотрим достаточно общий случай последовательной LRC цепи.
Запишем уравнение цепи 
. Чтобы избавиться от знака интеграла возьмём производную 
. Для записи характеристического уравнения заменим символы производных на множитель р в соответствующей степени, т.е. 
. Найдём корни уравнения 
, 
, где 
, а 
.
Частные случаи.
1. 
. В этом случае оба корня действительные и отрицательные. Следовательно, значение тока будет иметь вид 
. Постоянные интегрирования определяются по начальным условиям.
2. 
. В этом случае оба корня равны друг другу. Следовательно, значение тока будет иметь вид 
.
3. 
. В этом случае оба корня являются комплексными сопряжёнными 
, 
. Следовательно, значение тока будет иметь вид 
.
4. 
. В этом случае оба корня являются мнимыми сопряжёнными 
, 
. Следовательно, значение тока будет иметь вид
.
Аналогичным образом рассматривается и анализируется любая иная, например RC, цепь.
Для неё, соответственно, имеем: уравнение цепи- 
; производная - 
; характеристическое уравнение - 
; корень - 
; вид искомого уравнения тока - 
.
Для более сложных цепей приходится записывать и решать системы уравнений. В настоящей работе предлагается также определить колебательный процесс с тремя накопителями энергии. Так как определение корней для уравнений третьего и выше порядков затруднительно, предлагаем воспользоваться готовыми формулами
; 
, где 
.
Виртуальные исследования
|
|
|
