Испытание стального образца на внецентренное сжатие

Цель работы: проверить закон распределения нормальных напряжений в поперечном сечении, в зависимости, от эксцентриситета приложения сжи­мающей силы.

Внецентренное растяжение – сжатие имеет место в том случае, когда внешняя продольная сила смещена относительно оси бруса на некоторую величину.

Если точка приложения внешней продольной силы F смещена отно­сительно оси бруса на величину e (рис.37, а), но находится на главной центральной оси инерции z, то, приводя ее к центру тяжести поперечного сечения в соответствии с законами механики, получим осе­вую силу F и изгибающий момент M_у = F·е относительно оси у (рис.37, б).

Таким образом, в данном случае внецентренное сжатие сводится к осевому сжатию и плоскому изгибу в главной плоскости xz.

В общем случае, когда точка приложения продольной силы F не расположена на главных центральных осях инерции (рис.38), внецент­ренное растяжение – сжатие сводится к осевому растяжению – сжатию и двум плоским изгибам в главных плоскостях xy и xz.

Нормальные напряжения при внецентренном растяжении – сжатии в произвольной точке поперечного сечения с координатами у и z определяются по формуле

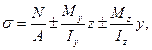(54)

где N – продольная сила, M_y=F·z_F, M_z=F·y_F – изгибающие моменты относительно осей y и z, y_F и z_F – координаты точки приложения силы F, A – площадь поперечного сечения бруса, I_y и I_z – моменты инерции сечения бруса.

Наибольшие напряжения возникают в точках сечения, наиболее удаленных от нейтральной линии (н.л.). Положение нейтральной линии определяется отрезками a_y и a_z (рис.38), которые вычисляются по формулам

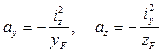(55)

Если y_F и z_F положительны, то, как следует из формул (55), величины a_y и a_z отрицательны, т.е. нейтральная линия всегда проходит через квадрант, противоположный квадранту точки приложения внешней силы.

В зависимости от координат точки приложения внешней силы y_F и z_F нейтральная линия может как пересекать сечение, так и нахо­диться за его пределами. В первом случае в сечении возникают напря­жения разных знаков, во втором – одного знака.

Ядром сечения называется область вокруг центра тяжести сечения, которая обладает следующим свойством: если точка приложения внешней силы F расположена внутри ядра сечения, то во всем сечении

возникают напряжения одного знака.

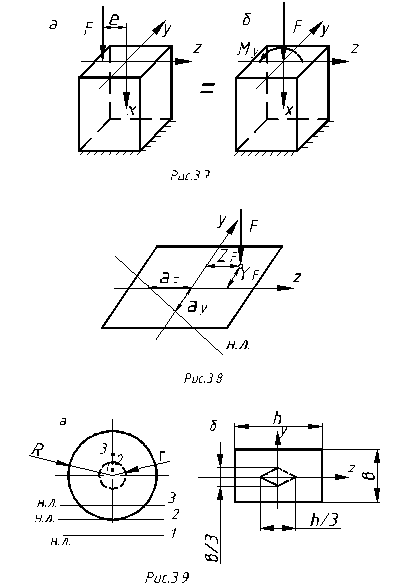Для бруса круглого поперечного сечения радиусом R ядром сече­ния является круг радиусом r= R/4 (рис.39, а), а для бруса пря­моугольного поперечного сечения размерами b 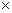h – ромб с диагоналями b/3 и h/3 (рис.39, б).

Если внешнюю силу приложить в точке 1 (рис.39, а), находящуюся внутри ядра сечения, то нейтральная линия будет находиться за преде­лами сечения (положение 1) и во всем сечении будут напряжения од­ного знака.

 

 

Если внешнюю силу приложить в точке 2 (на границе ядра сече­ния), то нейтральная линия будет касаться контура сечения (положе­ние 2). Напряжения во всем сечении также будут одного знака.

Если внешнюю силу приложить в тючке 3, то нейтральная линия (по­ложение 3) пересечет сечение и напряжения в сечении будут разных знаков.

 

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

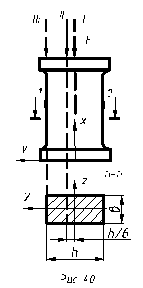
Испытания производятся путем сжатия на испытательной машине стального образца (рис.40) пря­моугольного поперечного сечения b 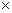h = 30 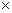60 мм.

На гранях образца, наиболее удаленных от оси z наклеены тензодатчики 1 и 2, база которых параллельна продольной оси образца.

В положении I образец подвергается осевому сжатию, а в положе­ниях II и III – осевому сжатию и плоскому изгибу в главной плоскос­ти xy, причем положение II соответствует приложению силы на грани­це ядра сечения.

 

Проведение испытания и обработка результатов

1. Записать начальные показания тензодатчиков N_1Н, N_2Н.

2. Плавно нагрузить образец усилием F = 50кН в положении I.

3. Записать конечные показания тензодатчиков N_1К, N_2К.

4. Разгрузить образец.

5. Вычислить относительные деформации по формуле (22).

6. Вычислить опытные напряжения по формуле закона Гука (20).

7. Вычислить нормальные напряжения в крайних точках поперечного се­чения (при y=h/2) по теоретической формуле (54) и пост­роить эпюру напряжений.

8. Вычислить расхождение в процентах между опытными и теоретически­ми значениями напряжений.

Аналогично выполнить все перечисленное для нагрузки в положе­ниях II и III.

РАБОТА №16

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: