 |
Проверка teopemы о взаимности перемещений
|
|
|
|
Цель работы. 1. Проверить справедливость теоремы о взаимности перемещений.
2. С помощью этой теоремы построить упругую линию консольной балки под действием сосредоточенной силы на конце.
Выделим на консольной балке два произвольных сечения 1 и 2 (рис.41, а, б).
Приложим в сечении 1 силу F (рис.41, а). Прогиб балки в сечении 2 под действием этой силы обозначим  .
.
Затем ту же силу F приложим в сечении 2 (рис.41, б). Прогиб балки в сечении 1 под действием этой силы обозначим  .
.
Теорема о взаимности перемещений устанавливает равенство между перемещениями  и
и  , т.е.
, т.е.
Теорема о взаимности перемещений является частным случаем теоремы о взаимности работ
 (57)
(57)
где F1 и F2 – силы, приложенные соответственно в сечениях 1 и 2.
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Испытания проводятся на той же установке, что и в лабораторной работе № 9. Для измерения прогибов используется индикаторы часового типа с ценой деления 0,01 мм.
Проведение испытания I и обработка результатов
1. Записать в журнал лабораторных работ длину консоли l и размеры поперечного сечения b и h (см. лаб. работу №9).
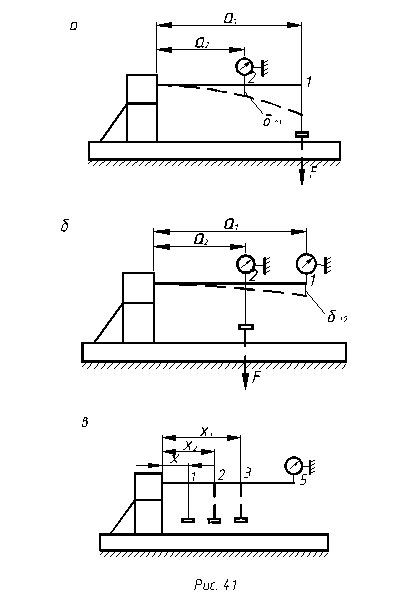
2. Выбрать две произвольные метки на балке и записать в журнал лабораторных работ расстояния a1 и a2 от заделки до этих меток.
3. Расположить (рис.41, а) подвеску для груза на расстоянии a1 от заделки.
4. Установить индикатор на расстоянии a2 от заделки и записать его начальное показание в делениях.
5. Установить на подвеску груз F =10 Н и записать новое показание индикатора в делениях.
6. По разности показаний и цене деления индикатора определить прогиб балки  в сечении 2.
в сечении 2.
Снять груз с подвески. Установить индикатор на расстоянии a1 от заделки (рис.41, б), а подвеску для груза – на расстоянии a2. Повторить опыт и определить прогиб балки  в сечении 1. Убедитесь, что
в сечении 1. Убедитесь, что  =
=  .
.
|
|
|
Проведение испытания 2 и обработка результатов
1. Установить индикатор на свободном конце балки (рис.41,в) и записать его начальное показание в делениях.
2. Расположить подвеску для груза на расстоянии x1= 10 см от заделки.
3. Установить на подвеску груз F = 10 Н и записать новое показание индикатора в делениях.
4. По разности показаний и цене деления индикатора определить прогиб балки  в сечении 5 под действием силы F =10 Н, приложенной в сечении 1. На основе теоремы о взаимности перемещений этот прогиб равен прогибу балки
в сечении 5 под действием силы F =10 Н, приложенной в сечении 1. На основе теоремы о взаимности перемещений этот прогиб равен прогибу балки  в сечении 1 под действием той же силы, но приложенной в сечении 5.
в сечении 1 под действием той же силы, но приложенной в сечении 5.
Устанавливая подвеску с грузом последовательно в сечениях 2, 3... (не изменяя положения индикатора) аналогично определить прогибы балки  ,
, 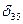 … в сечениях 2, 3,....
… в сечениях 2, 3,....
5. По данным опыта построить в масштабе изогнутую ось балки (упругую линию).
6. Вычислить прогибы  и
и  методом начальных параметров либо способом Верещагина.
методом начальных параметров либо способом Верещагина.
РАБОТА № 17
ИСПЫТАНИЕ ПРЯМОГО СТЕРЖНЯ
НА ПРОДОЛЬНЫЙ ИЗГИБ
Цель работа. 1. Провести наблюдение над явлением потери устойчивости.
2. Определить опытным путем величину критической силы и сравнить ее с результатами расчета по формуле Эйлера.
3.Вычислить критические напряжения и сравнить их с пределом пропорциональности.
Если прямолинейный стержень сжимать осевой силой F, то с возрастанием этой силы стержень вначале только укорачивается, сохраняя прямолинейную форму (рис.42, а), а затем наступает явление потери устойчивости – стержень изгибается (рис.42, б).
Нагрузка Fcr, превышение которой вызывает потерю устойчивости, называется критической.
Изгиб стержня при потере устойчивости происходит в плоскости наименьшей жесткости, т.е.поперечные сечения поворачиваются вокруг той оси, относительно которой момент инерции имеет минимальное значение. Возможные направления выпучивания стержней с различными поперечными сечениями указаны стрелками на рис. 43.
|
|
|
Если напряжения в сжатом стержне не превышают предела пропорциональности  , то величина критической силы определяется по формуле Эйлера
, то величина критической силы определяется по формуле Эйлера
 (58)
(58)
где E – модуль продольной упругости, Imin – минимальный момент инерции сечения, l – длина стержня,  – коэффициент приведения длины, учитывающий условия закрепления концов стержня (рис.44).
– коэффициент приведения длины, учитывающий условия закрепления концов стержня (рис.44).
Условие, при котором напряжения в сжатом стержне не превышают предела пропорциональности, а, следовательно, и условие применимости формулы Эйлера имеет место, если гибкость стержня 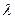 больше предельной гибкости
больше предельной гибкости  , т.е.
, т.е.
 (59)
(59)
где  – минимальный радиус инерции сечения, А – площадь поперечного сечения стержня.
– минимальный радиус инерции сечения, А – площадь поперечного сечения стержня.
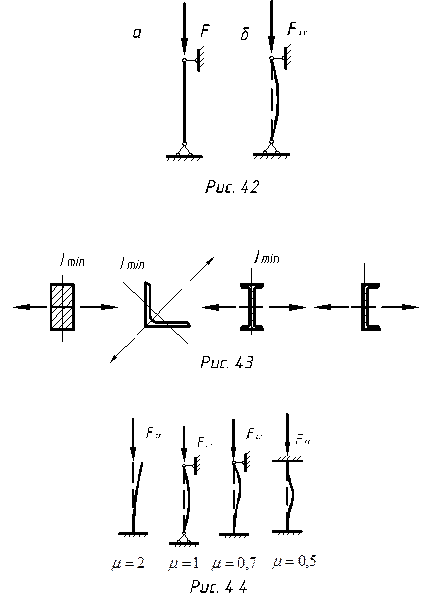
Величина предельной гибкости зависит от модуля продольной упругости Е и предела пропорциональности  и для стали Ст.3 имеет значение
и для стали Ст.3 имеет значение  =100. Следовательно, для стержней из стали Ст.3 формула Эйлера применима, если гибкость стержня
=100. Следовательно, для стержней из стали Ст.3 формула Эйлера применима, если гибкость стержня 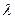 больше 100.
больше 100.
Критические напряжения в сжатом стержне определяются по формуле
 (60)
(60)
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Испытания производятся на специальной установке, схема которой приведена на рис.45. Стержень 1 прямоугольного поперечного сечения шарнирно закреплен по концам. На правой опоре расположен винт с рукояткой 2, с помощью которой производится нагружение стержня осевой сжимающей силой через толкатель 3. На левой опоре установлен динамометр 4 с индикатором часового типа для измерения величины сжимающей силы. Материал стержня – сталь Ст.3 с пределом пропорциональности  =200МПа.
=200МПа.
Проведение испытания
1. Записать в журнал лабораторных работ размеры стержня:
длинного l =100см, b 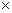 h = 3
h = 3 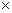 0,6 см
0,6 см
короткого l =50см, b 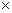 h = 3
h = 3 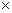 0,4 см
0,4 см

2. Установить индикатор динамометра на "0".
3. Медленно вращая рукоятку 2 (рис.45), нагружать стержень осевой сжимающей силой. При этом наблюдать за прогибом стержня. После того, как стержень получит заметный прогиб, убедитесь, что незначительное увеличение нагрузки (по показаниям индикатора) приводит к значительному увеличении прогиба.
4. Записать в журнал лабораторных работ показания индикатора в делениях.
|
|
|
5. Разгрузить установку, вращая рукоятку 2 в обратном направлении.
Обработка результатов испытания
1. По показанию индикатора определить опытную величину сжимающей силы Fcr с помощью тарировочной таблицы.
2. Вычислить критическую силу по формуле Эйлера (58).
3. Вычислить расхождение в процентах между опытным и теоретическим значением критической силы.
4. Вычислить критические напряжения по формуле (60) и сравнить их с пределом пропорциональности  .
.
СПИСОК ЛИТЕРАТУРЫ
1. Г.Беляев Н.М. Лабораторные работы по сопротивлению материалов. – М.: ГИТТЛ, 1956.-286 с.
2. Краткий справочник металлиста/Под ред. П.Н.Орлова и Е.А.Скороходова.
– М.: Машиностроение, 1986.-960 с.
3. Писаренко Г.С., Агарев В.А., Квитка А.Л., Попков В.Г., Уманский Э.С. Сопротивление материалов. – К.: Вища школа, 1986.-776 с.
4. Степин П.А. Сопротивление материалов. – М.: Высшая школа,1983.-303 с.
5. Тимошенко С.П. Сопротивление материалов. – М.: Наука, 1965.-Т.2.-430 с.
6. Феодосьев В.И. Сопротивление материалов. – М.: Наука, 1986.-512 с.
ОГЛАВЛЕНИЕ
Работа № 1. Испытание на растяжение стандартного стального образца....................3
Работа № 2. Испытание на сжатие пластичных и хрупких материалов.....................11
Работа № 3. Испытание на сжатие дерева.....................................................................15
Работа № 4. Испытание на срез стального и деревянного образцов..........................17
Работа № 6. Определение упругих постоянных материала.........................................20
Работа № 7. Опытное определение коэффициента концентрации напряжений........24
Работа № 8. Испытание стальной балки на поперечный изгиб...................................27
Работа № 9. Определение деформации балки при изгибе...........................................30
Работа №11. Испытание стального образца на кручение в пределах упругих
деформаций...............................................................................................34
Работа № 14. Испытание консольной балки на косой изгиб.......................................37
Работа №15. Испытание стального образца на внецентренное сжатие.....................41
Работа № 16. Проверка теоремы о взаимности перемещений....................................45
|
|
|
Работа № 17. Испытание прямого стержня на продольный изгиб.............................48
Список литературы.........................................................................................................52
Учебное издание
Сопротивление материалов. Методические указания к выполнению
лабораторных работ для студентов всех специальностей.
Составитель Потележко Виктор Пантелеевич
Компьютерная верстка студентов
Татарова Романа Константиновича,
Шемякина Руслана Николаевича
Подписано в печать. Формат 60 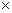 84/16. Усл. печ. л.. Уч.-изд. л. Тираж 300 экз. Заказ. Цена.
84/16. Усл. печ. л.. Уч.-изд. л. Тираж 300 экз. Заказ. Цена.
Отпечатано в Белгородском государственном технологическом университете В.Г.Шухова
308012, Белгород, Костюкова, 46.
|
|
|


