 |
Объем платных услуг образования и здравоохранения
|
|
|
|
Объем платных услуг образования и здравоохранения
|
Услуги | Объем платных услуг в текущих ценах, тыс. ден. ед. |
Изменение цен | |
| Базовый период | Отчетный период | ||
| Образование | +10 | ||
| Здравоохранение В том числе: хирургические терапевтические другие | +14 +17 +10 | ||
Сводный индекс цен по полному набору товаров-представителей, исчисленный по формуле цен Ласпейреса, — 0, 98.
Определим:
1) как изменились бы потребительские расходы населения на приобретение платных услуг образования и здравоохранения при неизменной структуре их потребления;
2) какие факторы оказали влияние на это изменение и в какой степени;
3) как изменилась стоимость жизни.
1. Изменение потребительских расходов населения в зависимости от изменения цен на платные услуги образования и здравоохранения при неизменной структуре их потребления позволяет определить индекс Ласпейреса по формуле (1):
(1)
Произведем необходимые расчеты (табл. 6).
Тогда
Таблица 6
Расчетные данные
| Услуги | Индивидуальные индексы цен, ip | Доля каждого вида платных услуг в общем объеме платных услуг образования и здравоохранения в базовом периоде,
|
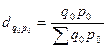
| Образование | 1, 10 | 1400: 2750 = 0, 509 |
| Здравоохранение В том числе: хирургические терапевтические другие | 1, 14 1, 17 1, 10 | 700: 2750 = 0, 255 350: 2750 = 0, 127 300: 22750 = 0, 109 |
Тогда
Потребительские расходы населения увеличились бы на 11, 9% только за счет изменения цен на платные услуги образования и здравоохранения при неизменной (на уровне базового периода) структуре.
|
|
|
2. Индекс цен Ласпейреса характеризует изменение стоимости в данном случае платных услуг образования и здравоохранения исключительно за счет изменения цен на эти услуги, так как структура их, зафиксированная на уровне базового периода, остается неизменной в течение некоторого промежутка времени. Следовательно, целью расчета этого индекса является изменение динамики стоимости базового (неизменного) объема услуг.
3. Изменение стоимости жизни позволяет установить все тот же индекс цен Ласпейреса, который так и называют индексом стоимости жизни или индексом потребительских цен, но расчет его в этом случае должен учитывать изменение цен по всем товарам-представителям, которые составляют так называемую потребительскую корзину. В условии задачи такой индекс равен 0, 98. Таким образом, стоимость жизни населения снизилась на 2%.
Теперь построим сводный индекс розничных цен на платные услуги образования и здравоохранения, используя индекс цен Пааше, в котором в качестве весов выступает продукция текущего периода (2):
. (2)
Тогда
.
Услуги образования и здравоохранения стали дороже на 11, 96% в отчетном периоде по сравнению с базовым, это подорожание составило 309 тыс. ден. ед. (2900 - 2591).
Способ абсолютных разниц является одной из модификаций элиминирования. При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на величину факторов базового периода (плановую), которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель.
|
|
|
Основная задача стохастического факторного анализа — определить степень влияния каждого фактора на уровень результативного показателя. Для этой цели используются способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа и т. д.
Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями. Отличают парную корреляцию (связь между двумя показателями, один из которых является факторным, а другой — результативным) и множественную корреляцию (возникает от взаимодействия нескольких факторов с результативным показателем). Исследование корреляционных соотношений имеет огромное значение. Факторный анализ дает возможность установить место и роль каждого фактора в формировании уровня исследуемых показателей. Расширяются знания об изучаемых явлениях, определяются закономерности их развития. В итоге — глубже обосновываются планы и управленческие решения, более объективно оцениваются результаты деятельности и точнее определяются необходимые резервы.
Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой 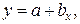(3):
(3)
где х — факторный показатель;
у — результативный показатель;
а и b — параметры уравнения регрессии, которые требуется отыскать.
Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание значений результативного показателя.
В качестве примера для иллюстрации корреляционного анализа прямолинейной зависимости могут быть использованы сведения об изменении потребления населением, например, мяса и мясопродуктов (у) в зависимости от среднедушевого дохода в месяц (х) (табл. 4).
|
|
|
Значения коэффициентов а и bнаходят из системы уравнений, полученных по способу наименьших квадратов.
В данном случае система уравнений имеет следующий вид:
(4)
где п— количество наблюдений (в нашем примере - 6).
Значения 
- рассчитываются на основе фактических исходных данных (табл. 7). Подставив полученные данные значения в систему уравнений, получим:
Умножив все члены первого уравнения на 1884 (11 304 / 6), получим следующую систему уравнений:
Отнимем от второго уравнения первое.
Отсюда:
6 071 720 b =74 562;
b=0, 012;
а =[292 - (11 304 × 0, 012)] / 6 = 26, 059.
Таким образом, уравнение связи, которое описывает зависимость потребления мяса и мясопродуктов от среднедушевого денежного дохода, будет иметь вид:
у = 26, 059 + 0, 012х.
Таблица 7
|
|
|
