 |
Порядок выполнения работы.
|
|
|
|
1. Наматывая на шкив шнур, поднять груз на высоту 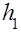 .
.
2. Отпустить груз и секундомером измерить время падения груза с высоты 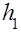 .
.
3. Определить высоту 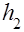 , на которую поднимается груз после опускания.
, на которую поднимается груз после опускания.
4. Измерить штангенциркулем радиус шкива  и вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11). Полученные результаты занести в таблицу. Повторить опыты при других значениях
и вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11). Полученные результаты занести в таблицу. Повторить опыты при других значениях 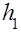 или массы
или массы  груза.
груза.
| № опыта | 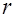
| 
| 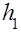
| 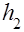
| 
| 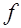
| 
| 
| 
| Е,% | Е,% |
Контрольные вопросы
1. Что называют моментом инерции материальной точки, твердого тела относительно оси вращения? В каких единицах измеряется?
2. Что называется моментом силы относительно оси вращения?
Как записывается основной закон динамики для вращательного движения?
3. Чему равна кинетическая энергия вращающегося тела?
4. Как определить линейное ускорение груза и угловое ускорение колеса?
5. Какой закон положен в основу вывода расчетных формул?
Литература
1. Курс общей физики. Том 1. Савельев И.С.
2. Курс физики. Том 1. Яворской Б.М., Детлаф А.А.
3. Курс общей физики. Шубин И.В.

ЛАБОРАТОРНАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО РАСТЯЖЕНИЮ ПРОВОЛОКИ
Цель работы: практическое изучение закона Гука.
Задача: определить практически модуль Юнга по растяжению стальной
проволоки.
Приборы и принадлежност и: 1.Стальная проволока
2.Микроскоп отсчетный "МИР".
3.Микрометр.
4.Грузы.
Краткая теория
Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества.
|
|
|
Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил.
В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает.
Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу.
Физическая величина, численно равная упругой силе  , приходящейся на единицу площади
, приходящейся на единицу площади  сечение тела, называется напряжением:
сечение тела, называется напряжением:

Английский физик Р. Гук экспериментально установил, что напряжение  при упругих деформациях тела прямо пропорционально его относительной деформации
при упругих деформациях тела прямо пропорционально его относительной деформации 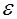 :
:
 , (1)
, (1)
где  - модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например,
- модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например,  ;
;
 ;
;  ;
;  .
.
Относительная деформация равна отношению абсолютной деформации  к начальной длине
к начальной длине  :
:
 (2)
(2)
Рассмотрим упругую деформацию одностороннего растяжения проволоки (рис. 1)
 К нижнему концу закрепленной проволоки длиной
К нижнему концу закрепленной проволоки длиной  и площадью поперечного сечения
и площадью поперечного сечения 
приложим силу  , под действием которой
, под действием которой
 проволока получит абсолютное удлинение
проволока получит абсолютное удлинение 

и в ней возникнет сила упругости 
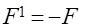 .
.
По закону Гука напряжение  , возникшее в
, возникшее в
проволоке, прямо пропорционально относительной

 деформации:
деформации:
 (1),
(1),
 отсюда модуль Юнга равен:
отсюда модуль Юнга равен:
Рис. 1 Е = 
 (2)
(2)
Если положить, что  , т.е.
, т.е.  , то
, то  , т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
, т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
|
|
|
Заменив в формуле (2) напряжение и относительное удлинение по формулам 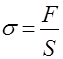 и
и  , получим:
, получим:
 (3)
(3)
Площадь поперечного сечения проволоки  (4), где
(4), где  диаметр проволоки.
диаметр проволоки.
Подставив выражение (4) в (3) и учитывая, что  , получим расчетную формулу для модуля Юнга:
, получим расчетную формулу для модуля Юнга:
 (5)
(5)
Порядок выполнения работы
1. Отметим на исследуемой проволоке какую-нибудь точку, для чего укрепим на ней кусочек тонкой проволоки.
2. Наведем на эту точку отсчетный микроскоп и заметим деление  на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой
на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой  .
.
3. Определяем удлинение проволоки, вызванное нагрузкой  ,
,

Здесь  пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение
пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение  , которое указано в таблице на установке.
, которое указано в таблице на установке.
4. Вычисляем модуль Юнга по формуле (5), значение  и
и  указаны на табличке возле установки.
указаны на табличке возле установки.
5. Опыты повторить с другими значениями масс  ,
,  .
.
6. Результаты опытов занести в таблицу:
| № опыта | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 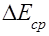
| 
| 
|

Контрольные вопросы
1.Что называется деформацией, виды деформаций?
2.Какими величинами характеризуют деформацию растяжения (сжатия)?
3.Как читается закон Гука и для каких деформаций он справедлив?
4.Какой физический смысл модуля Юнга?
Литература.
1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. "Курс физики" ч.1.
2. Шубин А.С. "Курс общей Физики".
3. Грабовский Р.И. "Курс физики".
ЛАБОРАТОРНАЯ РАБОТА № 4
|
|
|


