 |
Определение коэффициента внутреннего трения газа, средней длины свободного пробега и эффективного диаметра его молекул
|
|
|
|
Цель работы: практическое изучение одного из экспериментальных физических методов определения вязкости – метода Пуазейля.
Задачи работы:
1. Рассчитать коэффициент внутреннего трения (вязкость) воздуха, среднюю длину свободного пробега и эффективный диаметр молекул воздуха.
2. Исследовать зависимость коэффициента внутреннего трения газа от температуры.
Приборы и принадлежности: стеклянный баллон с краном в нижней части, капилляр, помещенный в электронагреватель, источник питания электронагревателя, секундомер, мерный и запасной стаканчики.
Теоретическое введение.
При движении слоев газа параллельно друг другу с различными по величине скоростями между ними возникают силы внутреннего трения (закон Ньютона)
,
где 
- коэффициент внутреннего трения газа (динамическая вязкость);
- градиент скорости;
S – площадь соприкосновения слоев;
Чтобы понять происхождение силы внутреннего трения, рассмотрим два соприкасающихся слоя газа, движущихся с различными скоростями 
и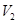 
.
Каждая молекула газа участвует в двух движениях: хаотическом тепловом со средней скоростью 
и упорядоченном движении со скоростью V. Вследствие хаотического теплового движения происходит непрерывный переход молекул из одного слоя в другой
Попав в другой слой, молекула сталкивается с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося с большей скоростью), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося с меньшей скоростью). В итоге импульс более быстро движущегося слоя убывает, а более медленно движущегося возрастает. Слои ведут себя так, как если бы к первому слою (скорость которого больше) была приложена тормозящая его движение сила, а ко второму слою (скорость которого меньше) – такая же по величине ускоряющая сила.
|
|
|
Теория метода
Для измерения коэффициента динамической вязкости воздуха в данной работе используется метод Пуазейля (метод основан на определении скорости истечения жидкости или газа через капилляр). Если открыть кран К 
, то вследствие вытекания воды из баллона давление воздуха будет уменьшаться и в него будет через капилляр засасываться воздух. Объем V газа, протекающего через капиллярную трубку радиуса r за время t, определяется по формуле Пуазейля:
,
где - коэффициент внутреннего трения или динамическая вязкость газа,
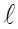- длина капилляра, 
- разность давлений на его концах
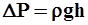
Здесь g – ускорение свободного падения, h – разность столбов жидкости в манометре,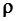 
-плотность воды (1000 
)
Из этой формулы получается выражение для :
(1)
Здесь все величины доступны измерению, что позволяет экспериментально определять коэффициент внутреннего трения.
Коэффициент внутреннего трения связан со средней длиной 
свободного пробега молекул, плотностью 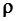газа и средней арифметической скоростью 
молекул газа соотношением: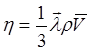 
(2)
Средняя арифметическая скорость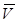 
молекул определяется по формуле:
(3)
Плотность 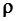газа можно найти, воспользовавшись уравнением состояния газа:
, отсюда 
, (4)
где P и T – давление и температура газа.
Решая совместно уравнения (2), (3) и (4), получим формулу для расчета средней длины свободного пробега молекул газа:
, (5)
где R – универсальная газовая постоянная;
- молярная масса газа (для воздуха 
);
P – давление газа (в условиях данной задачи его можно считать равным 10 
Па)
Из молекулярно-кинетической теории известно, что
Отсюда найдем эффективный диаметр молекулы газа:
|
|
|
, (6)
где k – постоянная Больцмана.
|
|
|
