Ср.арифмет-я величина. Ее св-ва и сп-бы вычисления.

Средняя арифметическая — такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным это среднее слагаемое. Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов х и частот f.

Средняя арифметическая бывает простая и взвешенная.

Средняя арифметическая простая применяется, если отдельное значение признака встречается 1 раз или одинаковое число раз. Она равна сумме отдельных значений признака хi, деленной на число этих значений n:.

Средняя арифметическая взвешенная используется если значения признака варианты встречаются неодинаковое число раз, то:, где хi — варианты значений признака, fi — частота.

Основные свойства средней арифметической:

1. От уменьшения или увеличения частот каждого значения признака х в n раз величина средней арифметической не изменится. Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.

2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

3. Средняя суммы разности двух или нескольких величин равна сумме разности их средних:

4. Если х = с, где с — постоянная величина, то.

5. Сумма отклонений значений признака x от средней арифметической х равна нулю:

Средняя гармоническая величина

Средняя гармоническая — это величина, обратная средней арифметической. В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная.

При работе со сгруппированными данными используется средняя гармоническая взвешенная.

Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной. Средняя гармоническая взвешенная используется в тех случаях, когда известен числитель исходного соотношения средней, но не известен знаменатель.

Если известен ряд вариант х и ряд произведений вариант на частоту xf = M, а сама частота f неизвестна, расчет средней производится по средней гармонической взвешенной:

Если исходные данные несгруппированны, то применяется средняя гармоническая простая. Средняя гармоническая простая используется при М = const:

Среднюю гармоническую простую называют еще средней из обратных значений признаков.

С помощью гармонической средней в статистике определяется средний % выполнения плана по данным фактического выполнения плана, средние затраты времени на выполнение операций по данным о средних затратах времени на одну операцию и общее время работы по отдельным работникам и т.д.

16. Виды средних величин, сп-бы расчета и их применение.

На этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.

Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.

Если исследуется совокупность с качественно однородными признаками, то средняя величина выступает здесь как типическая средняя. Например, для групп работников определенной отрасли с фиксированным уровнем дохода определяется типическая средняя расходов на предметы первой необходимости, т.е. типическая средняя обобщает качественно однородные значения признака в данной совокупности, каковым является доля расходов у работников данной группы на товары первой необходимости.

При исследовании совокупности с качественно разнородными признаками на первый план может выступить нетипичность средних показателей. Такими, к примеру, являются средние показатели произведенного национального дохода на душу населения (разные возрастные группы), средние показатели урожайности зерновых культур по всей территории России (районы разных климатических зон и разных зерновых культур), средние показатели рождаемости населения по всем регионам страны, средние температуры за определенный период и т.д. Здесь средние величины обобщают качественно разнородные значения признаков или системных пространственных совокупностей (международное сообщество, континент, государство, регион, район и т.д.) или динамических совокупностей, протяженных во времени (век, десятилетие, год, сезон и т.д.). Такие средние величины называют системными средними.

Таким образом, значение средних величин состоит в их обобщающей функции. Средняя величина заменяет большое число индивидуальных значений признака, обнаруживая общие свойства, присущие всем единицам совокупности. Это, в свою очередь, позволяет избежать случайных причин и выявить общие закономерности, обусловленные общими причинами.

На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.

Используются две категории средних величин:

o степенные средние;

o структурные средние.

Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.

Вторая категория (структурные средние) - это мода и медиана. Эти виды средних будут рассмотрены в теме «Ряды распределения».

Введем следующие условные обозначения:

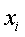- величины, для которых исчисляется средняя;

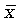- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;

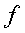- частота (повторяемость индивидуальных значений признака).

Различные средние выводятся из общей формулы степенной средней:

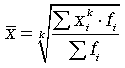(5.1)

при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k = 0 - средняя геометрическая; k = -2 - средняя квадратическая.

Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней.

Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

Формула средней арифметической (простой) имеет вид

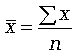(5.2)

где n - численность совокупности.

Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:

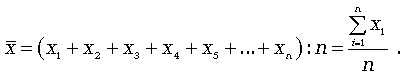
Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:

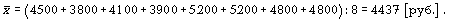
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид

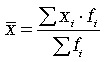
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:

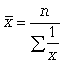
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид

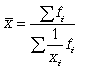
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель

Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для простой средней геометрической

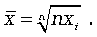
Для взвешенной средней геометрической

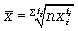Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула простой средней квадратической

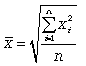
Формула взвешенной средней квадратической

В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:

а) установление обобщающего показателя совокупности;

б) определение для данного обобщающего показателя математического соотношения величин;

в) замена индивидуальных значений средними величинами;

г) расчет средней с помощью соответствующего уравнения.

12. Общ.пон-е о вариации пр-ка. Постр-е вариац.рядов и их граф.изобр-е.

13. Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.

14. Для измерения вариации признака используют как абсолютные, так и относительные показатели.

15. К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.

16. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.

17. Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:

18. 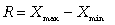(6.1)

19. Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели.

110. Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.

111. Формула среднего линейного отклонения (простая)

11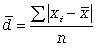2. (6.2)

113. Формула среднего линейного отклонения (взвешенная)

114. (6.3)

115. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение 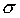и среднее квадратическое отклонение в квадрате , которое называют дисперсией.

116. Средняя квадратическая простая

117. 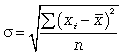(6.4)

118. Средняя квадратическая взвешенная

119. 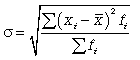(6.5)

120. Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.

121. Формулы дисперсии взвешенной и простой :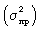

122. 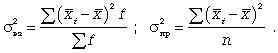(6.6)

123. Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях.

124. Данные показатели рассчитываются как отношение размаха вариации к средней величине признака ( коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака ( линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака ( коэффициент вариации) и, как правило, выражаются в процентах.

125. Формулы расчета относительных показателей вариации:

126. 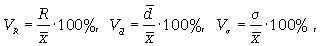(6.7)

127. где V_R - коэффициент осцилляции; - линейный коэффициент вариации; - коэффициент вариации.

128. Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака.

129. В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности.

130.

131. Наиболее употребительными графиками для изображения вариационных рядов, т. е. соотношений между значениями признака и соответствующими частотами или относительными частотами, являются полигон, гистограмма и кумулята.

132. Полигон чаще всего используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат на оси абсцисс в произвольно выбранном масштабе откладывают значения аргумента, т. е. варианты, а на оси ординат также в произвольно выбранном масштабе - значения частот или относительных частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность, и чтобы рисунок имел желательный размер. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю "левую" точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю "правую" точку также соединяют с точкой оси абсцисс.

Учеб. достиж-я уч-ся некот. класса хар-ся данными, представленными в т-це:

Количество баллов x

Число учащихся n

 

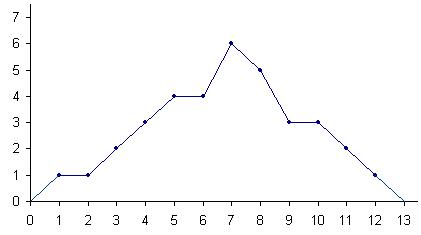
Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: