Аналитические показатели рядов динамики. Сп-бы их расчета.

Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента. Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, базисным. Для расчета показателей анализа динамики на постоянной базе, каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые, при этом, показатели называются базисными. Для расчета показателей анализа динамики на переменной базе, каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.

Абсолютный прирост:

1. базисный

2. цепной

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени

Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени, исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности отличаются только единицами измерения. Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть (долю) уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Коэффициент роста:

1. базисный:

2. цепной:

Темп роста:

1. базисный:

2. цепной:

Таким образом,

Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах или в долях единицы (коэффициенты прироста).

Темп прироста:

1. базисный:

2. цепной:

Темп прироста:

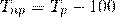
Коэффициент прироста:

Значение 1%

А% = Δу/Тпр(ц)
26.Средние показатели рядов динамики.

Система средних показателей динамики включает: - средний уровень ряда, - средний абсолютный прирост, - средний темп роста, - средний темп прироста.

Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней арифметической, т.е. по средней исчисленной из значений, изменяющихся во времени. Для интервальных рядов динамики при равных интервалах применяется средняя арифметическая простая:

где у – абсолютные уровни ряда,

п – число уровней ряда;

при неравных интервалах – средняя арифметическая взвешенная:

где у1,…уп – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t1,…tn – веса, длительность интервалов времени между смежными датами.

Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:

где у1,…уn – уровни ряда в последовательные моменты времени;

n – число уровней;

Средний уровень моментных рядов с неравными промежутками между временными датами определяется по формуле средней арифметической взвешенной:

Обобщающий показатель скорости изменения уровней во времени – средний абсолютный прирост (убыль), представляющий собой обобщающую характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую:

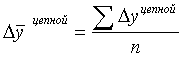
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу можно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по цепному способу):

где n – число коэффициентов;

П – знак произведения.

Средний коэффициент роста для равностоящих рядов динамики (по базисному способу):

где n – число уровней ряда динамики в изучаемом периоде, включая базисный.

Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста вычитанием из последних 100%. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:

27.Ст.м-ды выяв-я тенд-йВразв-иЯвл-й(м-д укрупн-я инт-в, скольз.ср-й, ан.выравн-е дин.ряда).

Закономерности изменения явления во времени не проявляются в каждом конкретном уровне ряда. Это связано с действием на явления общих и случайных причин. Поэтому в статистике для выявления закономерности или тенденции развития явления используют следующие методы обработки рядов динамики:

1. Метод сглаживания путем укрупнения интервалов во времени.

2. Выравнивание рядов динамики методом скользящей средней.

3. Метод аналитичного выравнивания.

Сущность приема укрепления интервалов сводится к следующему:

I прием. Первоначальный ряд динамики преобразуется и заменяется другим рядом, в котором показатели относятся к большим по продолжительности периодам времени, т.е. интервал укрупнен. Этот прием используется только для интервальных рядов динамики. Укрупнение производится до тех пор, пока не будет выявлена четкая тенденция развития явления, а уровни ряда охватывать большие периоды времени.

II прием. Метод скользящей средней заключается в следующем: формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня ряда на один уровень. По укрупненным интервалам определяем среднюю из уровней, входящих в каждый интервал.

Недостатки:

1. Невозможность получения всех уровней для сглаженного ряда. Число уровней в сглаженном РД меньше, чем в исходном, на (к – 1), где к – число периодов в укрупненном интервале (5 – 1) = 4, т. е. на 4.

2. Произвольность выбора интервала для определения скользящей средней.

III прием: Аналитическое выравнивание. При исчислении этого метода фактические уровни РД заменяются теоретическими, вычисленными на основе уравнения определенной кривой, отражающей общую тенденцию развития явления.

Тенденцию развития социально-экономических явлений обычно изображают кривой, параболой, гиперболой и прямой линией.

Если РД выравнивают по прямой, то уравнение прямой имеет следующий вид:

,

где у – фактические уровни;

у_t – теоретическое значение уровня;

t – периоды времени – фактор времени.

«а» и «в» – параметры уравнения.

28.Прогнозир-е рядов дин-ки и изуч-е сезонн.колеб-й в рядах динамики.

Динамическим рядом (рядом динамики) называются ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке и описывающих процесс развития, движения социально-экономических явлений и процессов во времени.

Относящиеся к отдельным периодам или датам значения признака – это уровни динамического ряда (y_i), периоды или даты, за которые представлены значения показателя – это показатели времени (t_i).

Принципы построения цепных и базисных показателей динамики:

1. Базисные показатели: каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения.

2. Цепные показатели: каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим, такое сравнение называют иногда сравнением с переменной базой.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени:

,

где – уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени . Определение теоретических (расчетных) уровней производится на основе так называемой адекватной математической модели,которая наилучшим образом отображает (аппроксимиру­ет) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражаю­щими тенденцию развития, являются:

линейная функция – прямая

,

показательная функция

;

степенная функция – кривая второго порядка (парабола)

,

где , , – параметры уравнений.

Показателем адекватности математической функции является стандартизованная ошибка аппроксимации

,

где – теоретические значения ряда динамики, n – число уровней ряда.

Для решения вопроса, какая из моделей является наиболее адекватной, сравниваются их стандартизованные ошибки аппроксимации.

Расчет параметров функции обычно производится методом наименьших квадратов (МНК), в котором в качестве решения принима­ется точка минимума суммы квадратов отклонений между тео­ретическими и эмпирическими уровнями:

,

где – выравненные (расчетные) уровни; — фактические уровни.

Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:

1) используя полусумму уровней, расположенных рядом с интерполируемыми;

2) по среднему абсолютному приросту;

3) по темпу роста.

Способ определения количественных значений за пределами ряда называют экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем.

Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.

29.Общее понятие об индексах. Индивидуальные индексы.

Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве.

Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают как относительные величины динамики.
Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы.
В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.

Статистика осуществляет классификацию индексов по следующим признакам:

1. В зависимости от объекта исследования:

· индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)

· индексы качественных показателей (индексы цен, себестоимости, заработной плата)

К индексам объемных показателей относятся индексы физического объема: товарооборота, продукции, потребления материальных благ и услуг; а также других показателей, имеющих количественный характер: численности работников, посевных площадей и т.п. К индексам качественных показателей относятся индексы: цен, себестоимости продукции, заработной платы, производительности труда, урожайности и т.п.;

2. По степени охвата элементов совокупности:

· индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)

· общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)

3. В зависимости от методологии исчисления общие индексы подразделяются на:

· агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).

· средние (являются производными от агрегатных)

4. В зависимости от базы сравнения различают:

· базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)

· цепные (если база сравнения постоянно меняется)

ИНДИВИДУАЛЬНЫЕ

В каждом индексе выделяют 3 элемента:

· индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс

· сравниваемый уровень — это тот уровень, который сравнивают с другим.

· базисный уровень — это тот уровень, с которым производится сравнение.

 индекс физического объема продукции:

iq=q1/q0

где q 1и q 0– количество произведенной продукции в отчетном и базисном периодах

Таким же образом рассчитывается индивидуальный индекс цен, себестоимости, трудоёмкости и др.

Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:

ipq=p1q1/p0q0

Однородные явления можно непосредственно суммировать и исчислять индексы, характеризующие изменение не одного элемента, а группы элементов или всей совокупности в целом. Такие индексы называются общими индексами. Например:

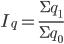
⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: