 |
Показатели центра распределения и методы их расчета.
|
|
|
|
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, средняя арифметическая, средняя геометрическая, средняя гармоническая, степенные средние, взвешенные средние, медиана, мода.
Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.
Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.
Для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле
где n – ч-ло ед-ц в сов-ти. Ф-ла медианы: 
где xМе - нижняя граница медианного интервала; i - величина интервала; S-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала.
Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.
Чтобы найти конкретное значение моды, необходимо использовать формулу
где xМо - нижняя граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным.
19.Показатели интенсивности вариации, асимметрии и эксцесса.
|
|
|
Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:
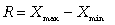(6.1)
Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели.
Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.
Формула среднего линейного отклонения (простая и взвешенная)
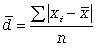
Среднее квадратическое отклонение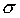 
и среднее квадратическое отклонение в квадрате 
, которое называют дисперсией.
Средняя квадратическая простая и взвешенная
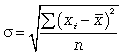
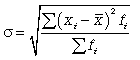
Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях.
Данные показатели рассчитываются как отношение размаха вариации к средней величине признака ( коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака ( линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака ( коэффициент вариации) и, как правило, выражаются в процентах.
|
|
|
Формулы расчета относительных показателей вариации:
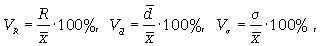(6.7)
где VR - коэффициент осцилляции; 
- линейный коэффициент вариации; 
- коэффициент вариации.
Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака.
Пок-ль асимметрии 
Пок-ль эксцесса 
As< 0.25 – слабая асимм-я, =0,25-0,5 – умерен.,> 0.5 – крайне асимметричное распределение
Если пок-ль эксцесса=0,то распр-е нормальное, если<0, то распределение плосковершинное, если>0, то островершинное.
20.Понятие о выборочном наблюдении. Причины его применения и преимущества.
Выборочное наблюдение основывается на применении выборочного метода статистического исследования. Сущность выборочного наблюдения состоит в том, что обследованию подвергается только часть совокупности, отобранная по особым правилам:
• должен действовать принцип случайного непредвзятого отбора
• в выборочную совокупность должны попасть представители всех групп, имеющихся в генеральной совокупности
• выборочная совокупность должна полно воспроизводить закономерности, присущие всей генеральной совокупности.
Генеральная совокупность — вся совокупность, из которой проводится отбор; отобранные данные из генеральной являются выборочной совокупностью или выборкой. Необходимая численность выборки рассчитывается по соответствующим математическим формулам.
Виды выборочных работ: • демографическое обследование; • социологическое обследование, опросы; • проверка качества готовой продукции; • определение потерь рабочего времени путем фотографии рабочего дня и др.
Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда.
Если в период обследования будут соблюдены все правила его научной организации, то выборочный метод даст довольно точны результаты, и поэтому данный метод целесообразно применять для проверки данных сплошного наблюдения.
Различают 2 вида выборочного наблюдения: повторный и бесповторный.
При бесповторном отборе отобранная единица не возвращается в совокупность, при повторном — возвращается и снова может быть выбранной.
|
|
|
Преимущества выборочного наблюдения: 1)экономия времени и средств (в результате сокращения объема работ); 2)сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве, испытания электрических лампочек на продолжительность горения, проверка консервов на доброкачественность); 3)высокая точность результатов обследования благодаря сокращению ошибок, происходящих при регистрации.
|
|
|
