 |
Решение задач в смешанных стратегиях (частный случай)
|
|
|
|
Решить игру - означает найти цену игры и оптимальные стратегии. Рассмотрение методов нахождения оптимальных смешанных стратегий для матричных игр начнем с простейшей игры, описываемой матрицей 2х2. Игры с седловой точкой специально рассматриваться не будут. Если получена седловая точка, то это означает, что имеются невыгодные стратегии, от которых следует отказываться. При отсутствии седловой точки можно получить две оптимальные смешанные стратегии. Как уже отмечалось, эти смешанные стратегии записываются так:
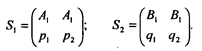
Значит, имеется платежная матрица
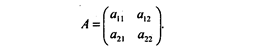
При этом
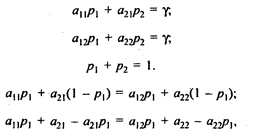
откуда получаем оптимальные значения 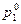 и
и 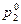 :
:
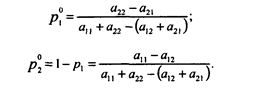
Зная 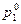 и
и 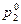 находим g:
находим g:
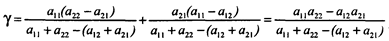
Вычислив g, находим 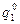 и
и  :
:
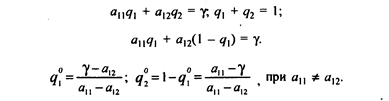
Задача решена, так как найдены векторы
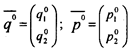
и цена игры g. Имея матрицу платежей А, можно решить задачу графически. При этом методе алгоритм решения весьма прост (рис. 2.1):
1. По оси абсцисс откладывается отрезок единичной длины.
2. По оси ординат откладываются выигрыши при стратегии А 1.
3. На линии, параллельной оси ординат, в точке 1 откладываются выигрыши при стратегии А 2.
4. Концы отрезков обозначаются для a11 – b11, a12 – b21, a22 – b22, a21 – b12 и проводятся две прямые линии b11 b12 и b21 b22.
5. Определяется ордината точки пересечения с. Она равна g. Абсцисса точки с равна р2 (р1 = 1 – р2).

Рис. 2.1. Оптимальная смешанная стратегия
Данный метод имеет достаточно широкую область приложения. Это основано на общем свойстве игр т´п, состоящем в том, что в любой игре т´п каждый игрок имеет оптимальную смешанную стратегию, в которой число чистых стратегий не больше, чем min(m,n). Из этого свойства можно получить известное следствие: в любой игре 2´п и т´2 каждая оптимальная стратегия  и
и 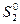 содержит не более двух активных стратегий. Значит, любая игра 2 ´n и т´2 может быть сведена к игре 2 ´ 2. Следовательно, игры 2 ´т и т´2 можно решить графическим методом.
содержит не более двух активных стратегий. Значит, любая игра 2 ´n и т´2 может быть сведена к игре 2 ´ 2. Следовательно, игры 2 ´т и т´2 можно решить графическим методом.
|
|
|
Если матрица конечной игры имеет размерность т´п, где т>2 и п>2, то для определения оптимальных смешанных стратегий, как будет показано в приложении, используется линейное программирование.
Рассмотрим некоторые практические задачи, в которых используются критерии игр для оценки наиболее эффективного поведения оперирующей стороны.
Задача 2.1. Выбрать оптимальный режим работы новой системы ЭВМ, состоящей из двух ЭВМ типов А1 и А2. Известны выигрыши от внедрения каждого типа ЭВМ в зависимости от внешних условий, если сравнить со старой системой.
При использовании ЭВМ.типов А1 и А2 в зависимости от характера решаемых задач В1 и В2 (долговременные и краткосрочные) будет разный эффект. Предполагается, что максимальный выигрыш соответствует наибольшему значению критерия эффекта от замены вычислительной техники старого поколения на ЭВМ А1 и А2.
Итак, дана матрица игры (табл. 2.4), где А1, А2 - стратегии руководителя; В1, В2 - стратегии, отражающие характер решаемых на ЭВМ задач.
Таблица 2.4
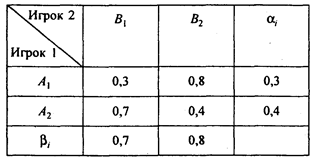
Требуется найти оптимальную смешанную стратегию руководителя и гарантированный средний результат g, т.е. определить, какую долю времени должны использоваться ЭВМ типов А1 и А2.
Решение. Запишем условия в принятых индексах:
а11 = 0,3; а12 = 0,8; а21 = 0,7; а22 = 0,4.
Определим нижнюю и верхнюю цены игры:
a1 = 0,3; a2 = 0,4; a = 0,4;
b1 = 0,7; b2 = 0,8; b = 0,7.
Получаем игру без седловой точки, так как
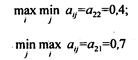
Максиминная стратегия руководителя вычислительного центра – А2.
Для этой стратегии гарантированный выигрыш равен a = 0,4 (40 %) по сравнению со старой системой.
Решение для определения g, р1 и р2 проведем графически (рис. 2.2).
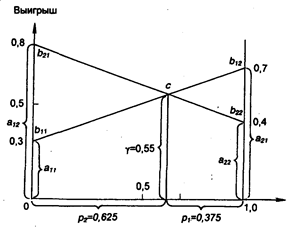
Рис. 2.2. Графическая интерпретация алгоритма решения
Алгоритм решения:
|
|
|
1. По оси абсцисс отложим отрезок единичной длины.
2. По оси ординат отложим выигрыши при стратегии А1.
3. На вертикали в точке 1 отложим выигрыши при стратегии А2.
4. Проводим прямую b11 b12, соединяющую точки а11,a21.
5. Проводим прямую b21b22, соединяющую точки а12, а22.
6. Определяем ординату точки пересечения с линий b11b12 и b 21 b 22. Она равна g.
7. Определим абсциссу точки пересечения с. Она равна р2, а р1=1–р2
Выпишем решение и представим оптимальную стратегию игры:

Вывод. При установке новой системы ЭВМ, если неизвестны условия решения задач заказчика, на работу ЭВМ А1 должно приходиться 37,5 % времени, а на работу ЭВМ А2 - 62,5 %. При этом выигрыш составит 55 % по сравнению с предыдущей системой ЭВМ.
|
|
|


