Ожидаемая ценность точной информации

Предположим, что консультационная фирма за определенную плату готова предоставить информацию о фактической ситуации на рынке в тот момент, когда руководству компании надлежит принять решение о масштабе производства. Принятие предложе­ния зависит от соотношения между ожидаемой ценностью (ре­зультативностью) точной информации и величиной запрошенной платы за дополнительную (истинную) информацию, благодаря которой может быть откорректировано принятие решения, т.е. первоначальное действие может быть изменено.

Ожидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной инфор­мации.

Рассчитаем ожидаемую ценность точной информации для примера, в котором дополнительное обследование конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было показано выше, максимальная ожидаемая денежная оценка равна:

ОДО = 0,5 * 100 000 - 0,5 * 20 000 = 40 000 дол.

Если точная информация об истинном состоянии рынка бу­дет благоприятной (ОДО =200 000 дол., см. табл. 3.1), принима­ется решение строить крупное производство; если неблагоприятной, то наиболее целесообразное решение - продажа патента (ОДО=10 000 дол.). Учитывая, что вероятности благоприятной и неблагоприятной ситуаций равны 0,5, значение ОДО_т.и (ОДО точной информации) определяется выражением:

ОДО_т.и = 0,5 * 200 000 + 0,5 * 10 000 = 105 000 дол.

Тогда ожидаемая ценность точной информации равна:

ОЦ_т.и = ОДО_т.и - ОДО = 105 000 - 40 000 = 65 000 дол.

Значение ОЦ_т.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об ис­тинном состоянии рынка в тот момент, когда ей это необходимо.

ЗАДАЧИ С РЕШЕНИЯМИ

Задача 3.5. Компания «Российский сыр» - небольшой произ­водитель различных продуктов из сыра на экспорт. Один из продуктов - сырная паста - поставляется в страны ближнего зарубежья. Генеральный директор должен решить, сколько ящи­ков сырной пасты следует производить в течение месяца. Веро­ятности того, что спрос на сырную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0,1; 0,3; 0,5; 0,1.

Затраты на производство одного ящика равны 45 дол. Компа­ния продает каждый ящик по цене 95 дол. Если ящик с сырной пастой не продается в течение месяца, то она портится и компа­ния не получает дохода. Сколько ящиков следует производить в течение месяца?

Решение. Пользуясь исходными данными, строим матри­цу игры. Стратегиями игрока 1 (компания «Российский сыр») являются различные показатели числа ящиков с сырной пас­той, которые ему, возможно, следует производить. Состояниями природы выступают величины спроса на аналогичное число ящиков.

Вычислим, например, показатель прибыли, которую получит производитель, если он произведет 8 ящиков, а спрос будет толь­ко на 7.

Каждый ящик продается по 95 дол. Компания продала 7, а произвела 8 ящиков. Следовательно, выручка будет 7*95, а из­держки производства 8 ящиков 8*45. Итого прибыль от указан­ного сочетания спроса и предложения будет равна: 7*95 - 8*45 = 305 дол. Аналогично производятся расчеты при других соче­таниях спроса и предложения.

В итоге получим следующую платежную матрицу в игре с природой (табл. 3.3). Как видим, наибольшая средняя ожидаемая прибыль равна 352,5 дол. Она отвечает производству 8 ящиков.

Таблица 3.3

 

* В скобках приведена вероятность спроса на ящики.

 

На практике чаще всего в подобных случаях решения принима­ются исходя из критерия максимизации средней ожидаемой прибы­ли или минимизации ожидаемых издержек. Следуя такому подходу, можно остановиться на рекомендации производить 8 ящиков, и для большинства ЛПР рекомендация была бы обоснованной. Именно так поступаем мы, когда в гл. 6 - 8 рассматриваем различные при­кладные задачи принятия решений в играх с природой.

Однако, привлекая дополнительную информацию в форме расчета среднего квадратичного отклонения как индекса риска, мы можем уточнить принятое на основе максимума прибыли или минимума издержек решение. Это в полной мере согласуется с характеристиками вариантов, представленных на рис. 1.1. Допол­нительные рекомендации могут оказаться неоднозначными, за­висимыми от склонности к риску ЛПР.

Вспомним необходимые для наших исследований формулы теории вероятностей [2, с. 109, 119]:

дисперсия случайной величины x, равна

Dx = M(x ² ) – (Mx) ²;

среднее квадратичное отклонение

где D и М - соответственно символы дисперсии и математического ожидания.

Проводя соответствующие вычисления для случаев производ­ства 6, 7, 8 и 9 ящиков, получаем:

6 ящиков

 

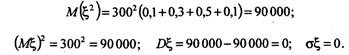
7 ящиков

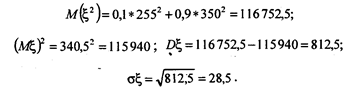
8 ящиков

9 ящиков

Вывод. Из представленных результатов расчетов с учетом полученных показателей рисков - средних квадратичных отклоне­нии - очевидно, что производить 9 ящиков при любых обстоятель­ствах нецелесообразно, ибо средняя ожидаемая прибыль, равная 317, меньше, чем для 8 ящиков (352,5), а среднее квадратичное откло­нение (76) для 9 ящиков больше аналогичного показателя для 8 ящиков (63,73). А вот целесообразно ли производство 8 ящиков по сравнению с 7 или 6 - неочевидно, так как риск при производстве 8 ящиков (sx = 63,73) больше, чем при производстве 7 ящиков (sx = 28,5) и тем более 6 ящиков, где sx = 0. Вся информация с учетом ожидаемых прибылей и рисков налицо. Решение должен принимать генеральный директор компании «Российский сыр» с учетом его опыта, склонности к риску и степени достоверности показателей вероятностей спроса: 0,1; 0,3; 0,5; 0,1. Авторы, учиты­вая все приведенные числовые характеристики случайной величи­ны - прибыли, склоняются к рекомендации производить 7 ящиков (не 8, что вытекает из максимизации прибыли без учета риска!). Читателю предлагается обосновать свой выбор.

Задача 3.6. Рассмотрим упомянутую выше проблему закупки угля для обогрева дома. Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома (табл. 3.4). Вероятности зим: мягкой - 0,35; обычной - 0,5; холодной - 0,15.

Таблица 3.4

Зима	Количество угля, т	Средняя цена за 1 т в ф. ст.
Мягкая
Обычная		7,5
Холодная

 

Эти цены относятся к покупкам угля зимой. Летом цена угля 6 ф. ст. за 1 т, у вас есть место для хранения запаса угля до 6 т, заготавливаемого летом. Если потребуется зимой докупить недо­стающее количество угля, докупка будет по зимним ценам. Пред­полагается, что весь уголь, который сохранится до конца зимы, в лето пропадет.* Сколько угля летом покупать на зиму?

* Предположение делается для упрощения постановки и решения задачи.

 

Решение. Построим платежную матрицу (табл. 3.5).

Таблица 3.5

 

Произведем расчет ожидаемой средней платы за уголь (табл. 3.6).

Таблица 3.6

Зима	Средняя ожидаемая плата
Мягкая	-(24*0,35+31,5*0,5+40*0,15)= -30,15
Обычная	-(30*0,35+30*0,5+38*0,15)= -31,2
Холодная	-(36*0,35+36*0,5+36*0,15)= -36

 

Как видим из табл. 3.6, наименьшая ожидаемая средняя пла­та приходится на случай мягкой зимы (30,15 ф. ст.). Соответ­ственно если не учитывать степени риска, то представляется целесообразным летом закупить 4 т угля, а зимой, если потребу­ется, докупить уголь по более высоким зимним ценам.

Если продолжить исследование процесса принятия решения и аналогично задаче 3.5 вычислить средние квадратичные откло­нения платы за уголь для мягкой, обычной и холодной зимы, то соответственно получим:

• для мягкой зимыsx = 5,357;

• для обычной зимы sx = 2,856;

• для холодной зимы sx = 0.

Минимальный риск, естественно, будет для холодной зимы, однако при этом ожидаемая средняя плата за уголь оказывается максимальной - 36 ф. ст.

Вывод. Мы склоняемся к варианту покупки угля для обыч­ной зимы, так как согласно табл. 3.6 ожидаемая средняя плата за уголь по сравнению с вариантом для мягкой зимы возрастает на 3,5 %, а степень риска при этом оказывается почти в 2 раза меньшей (sx = 2,856 против 5,357).

Отношение среднего квадратичного отклонения к математи­ческому ожиданию (средний риск на затрачиваемый 1 ф. ст.) для обычной зимы составляет = 0,0915 против аналогичного показателя для мягкой зимы, равного = 0,1777, т.е. вновь различие почти в 2 раза.

Эти соотношения и позволяют нам рекомендовать покупку угля, ориентируясь не на мягкую, а на обычную зиму.

Задача 3.7. АО «Фото и цвет» - небольшой производитель химических реактивов и оборудования, которые используются не­которыми фотостудиями при изготовлении 35-мм фильмов. Один из продуктов, который предлагает «Фото и цвет», - ВС-6. Пре­зидент АО продает в течение недели 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика АО получает 35 дол. прибыли. Как и многие фотографические реактивы, ВС-6 имеет очень малый срок годности. Поэтому, если ящик не продан к концу недели, он должен быть уничтожен. Каждый ящик обходится предприятию в 56 дол. Вероятности продать 11, 12 и 13 ящиков в течение недели равны соответственно 0,45; 0,35; 0,2. Как вы советуете поступить? Как вы порекомендуете поступить, если бы «Фото и цвет» мог сделать ВС-6 с добавкой, значительно про­длевающей срок его годности?

Решение. Матрицу игры с природой (здесь АО «Фото и цвет» - игрок с природой, а природа - торговая конъюнкту­ра) строим по аналогии с рассмотренными выше задачами (табл. 3.7).

Таблица 3.7

* В скобках приведены вероятности спроса на ящики.

 

Расчет средней ожидаемой прибыли производится с исполь­зованием вероятностей состояний природы, как и в задачах 3.5 и 3.6.

Вывод. Наибольшая из средних ожидаемых прибылей (385 дол.) отвечает при заданных возможностях спроса произ­водству 11 ящиков ВС-6.

Производство 11 ящиков в неделю и следует рекомендовать АО «Фото и цвет», ибо показатель риска - среднее квадратичное отклонение, как нетрудно убедиться, sx = 0 - минимален при максимальной средней ожидаемой прибыли.

Если срок службы химического реактива будет удлинен, то его производство даже при прежнем спросе можно увеличить, частично поставляя на склад для последующей реализации.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: