Задачи для самостоятельного решения.

Задача 2.2. Найдите седловые точки следующих платежных мат­риц:

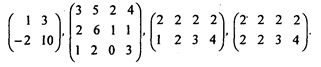
Задача 2.3. Найдите для платежной матрицы:

Задача 2.4. Решите аналитически и графически, используя поня­тие доминирования, игры, определяемые следующими платежными матрицами:

Задача 2.5. Постройте платежную матрицу двухпальцевой игры Морра, которая заключается в следующем. В игру играют два челове­ка: каждый из них показывает один или два пальца и одновременно называет число пальцев, которое, по его мнению, покажет его против­ник (естественно, противник этого не видит). Если один из игроков угадывает правильно, он выигрывает сумму, равную сумме пальцев, показанных им и его противником. В противном случае - ничья (вы­игрыш равен нулю).

Найдите нижнюю и верхнюю цены игры.

Задача 2.6. Используя понятие доминирования, уменьшите разме­ры следующей платежной матрицы:

Для задач 2.7-2.12 постройте платежную матрицу игры и сформу­лируйте соответствующую модель линейного программирования.

Задача 2.7. Пусть сторона А засылает подводную лодку в один из п районов. Сторона В, располагая т противолодочными кораблями, желает обнаружить лодку противника. Вероятность обнаружения лодки в j -м районе (j = 1 ,...,п) равна p_j. Предполагается, что обнаружение под­лодки каждым кораблем является независимым событием. Сторона В может посылать в различные регионы разное количество кораблей (рас­пределение т кораблей по регионам и есть стратегии стороны В). Сто­рона В стремится максимизировать вероятность обнаружения подлод­ки. Сторона А желает противоположного.

Вероятность обнаружения лодки в районе j, в котором находится r_ij кораблей (i - номер стратегии), равна:

причем . Найдите оптимальное распределение противолодоч­ных кораблей по регионам.

Рассмотреть частный случай: m = 2, п = 2, р₁ = 0,6, р₂ = 0,4.

Задача 2.8. Каждому из игроков выдается по бубновому и трефо­вому тузу. Игрок 1 получает также бубновую двойку, а игрок 2 - тре­фовую. При первом ходе игрок 1 выбирает и откладывает одну из своих карт, а игрок 2, не зная карты, выбранной игроком 1, также откладыва­ет одну из своих карт. Если были отложены карты одной масти, то выигрывает игрок 1, в противном случае выигравшим считается игрок 2. Если отложены две двойки, выигрыш равен нулю. Размер выигрыша определяется картой, отложенной победителем (тузу приписывается одно очко, двойке - два).

Задача 2.9. Фирма изготавливает железобетонные панели, исполь­зуя в качестве основного сырья цемент. В связи с неопределенным спросом на изделия потребность в сырье в течение месяца также не определена. Цемент поставляется в мешках, причем известно, что по­требность может составлять D₁,D₂,...,D_n мешков. Резервы сырья на складе могут составлять R₁,R₂,...,R_n мешков в месяц. Учитывая, что удельные затраты на хранение сырья равны с ₁ а удельные издержки дефицитности сырья (потери, связанные с отсутствием необходимого количества цемента на складе) равны с ₂, определить оптимальную стра­тегию управления запасами цемента на складе.

Рассмотреть частный случаи: п = 5, c₁ = 5, c₂ = 3;

D = (1 500, 2 000, 2 500, 3 500, 4 000), R = (1 500, 2 000, 2 500, 3 500, 4 000).

Задача 2.10. Игрок 2 прячет некоторый ценный предмет в одном из п мест, а игрок 1 этот предмет ищет. Если он его находит, то получает сумму а_i где i = 1,2,..., п, в противном случае - не получает ничего.

Задача 2.11. Два игрока независимо друг от друга называют по одному числу из диапазона 1 - 5. Если сумма чисел нечетная, то иг­рок 2 платит игроку 1 сумму, равную максимальному из чисел; если четная, то платит игрок 1.

Задача 2.12. Два игрока имеют по п рублей и предмет ценой с > 0. Каждый игрок делает заявку в запечатанном конверте, предлагая i руб. (где i - одно из целых чисел от 0 до п) за предмет. Записавший большее число получает предмет и платит другому предложенную им сумму. Если оба игрока заявляют одинаковую сумму, то предмет назначается без компенсирующего одностороннего платежа одному из игроков путем бросания монеты, так что ожидаемая доля каждого в предмете состав­ляет в этом случае половину с. Постройте платежную матрицу игры и определите, имеет ли игра седловую точку.